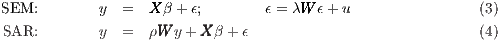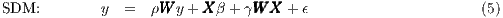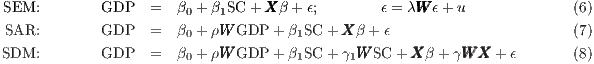Volume
3, Number 1, 2016, 1–24 journal homepage:
region.ersa.org
Volume
3, Number 1, 2016, 1–24 journal homepage:
region.ersa.orgDOI: 10.18335/region.v3i1.73
Social Capital and Economic Well-being in Germany’s Regions: An Exploratory Spatial Data Analysis
1 University of Bern, Bern, Switzerland (email: katrin.botzen@soz.unibe.ch) Received: 19 February 2015/Accepted: 1 March 2016Abstract. This article explores social capital in Germany in line with Putnam’s claim that social capital benefits regional economic well-being. In particular, this macro-level study examines whether the number of civic associations, as a measure of a vibrant civil society, is related to higher GDP. Since this study uses spatial data on civic associations and official statistics concerning the German NUTS-3 regions, different spatial matrices model interdependencies among the dependent units of analysis. Exploratory spatial data analysis illustrates spatial patterns between districts, as well as each variable’s radius of influence. Cross-sectional spatial models help examine social capital’s effect on regional economic well-being. Results of these analyses are two-fold: first, the geographical scope of social capital is locally concentrated, whereas the sphere of economic well-being encloses a wider area. Second, social capital correlates positively with economic well-being in Germany’s many regions.
Key words: social capital, civic associations, economic well-being, Germany, spatial interdependence
1 Introduction
Social capital is one of social science’s top exported concepts due to its easy transfer to and from daily life. Moreover, social capital is appealing to diverse research strategies and approaches because it is a multidimensional medley measured with different indicators, analysed with respect to different outcomes, and studied on different levels of analysis. Over the course of the last 25 years, social capital has become a widely used synonym for social contacts, networks, norms, and trust. This is based primarily on Putnam’s (1993, 2000) definition, who describes social capital as “features of social life – networks, norms, and trust – that enable participants to act together more effectively” (Putnam 1993, p. 664). Putnam emphasised “networks of civic engagement, like neighbourhood associations, choral societies, cooperatives, sports clubs, mass-based-parties [… as the] essential form of social capital” (Putnam 1993, p. 173). Members and even non-members can benefit from dense civic networks. For Putnam it is clear that “civic connections help make us healthy, wealthy, and wise” (Putnam 2000, p. 287), and that social capital in general is associated with a variety of individual and collective benefits. On a contextual level, communities and regions with dense social networks can be more productive, collaborate successfully, and perform more optimally.
Social scientists claim that social capital is an explanatory factor for prosperity; this highlights a social dimension in the economists’ perspective on wealth, and leads to a routinisation of social capital in economic development research (Woolcock 2010). Putnam (1993, 2000) tested his hypothesis that social capital enhances socio-economic well-being by analysing American and Italian regions. His maps have become quite well-known, which show differences of social capital indices across American states and Italian regions. Many social capital researchers followed this line of thought by analysing macro-units such as cities, states, regions, or countries, but their statistical analyses often neglect spatial dependence on units of analysis, with the result that the standard errors of the regression’s coefficients are underestimated. This means substantive interpretations may be misleading. The general principal that proximal regions are more intimately related, similar to each other, and are able to perform more successfully than more distant areas, should be transferable to social capital research as well. Regional embeddedness and proximity are substantial determinants for vibrant networks and face-to-face contacts, and therefore important for social capital (see section 2.3). However, research has thus far neglected spatial patterns and scopes of social capital. Indeed, this article addresses this neglect in delving into whether there are spatial interdependencies of social capital among macro-units and whether they are significant in explaining prosperity. Inspired by Putnam’s studies, this article investigates the relationship between economic well-being and social capital, specifically among subnational regions in Germany as the units of analysis. This work contributes to the literature by introducing unique data from an organisational census of civic associations, which are a structural indicator for social capital. Consequently, it conducts explorations of spatial patterns of regional social capital in Germany and examinations of its scopes for the first time. Lastly, it employs spatial regression models toward analysing social capital’s relation to wealth, and simultaneously capturing spatial dependence among German regions.
The outline of the paper is as follows. The second section discusses the relationship of social capital and economic well-being as well as the spatial dimension of both variables. The third part introduces data on Germany’s subnational regions. Section four describes the spatial patterns of economic well-being and social capital, appropriating them to discuss how spatial interdependence in Germany can be modelled. Section five exhibits diagnostic tests so as to detect spatial patterns; in particular, it applies local indicators and global measures of spatial association. The sixth section presents spatial regression models to analyse economic and social determinants of regional well-being and capture spatial correlations in the data. Moreover, it discusses limitations, and outlines avenues for further research, finally arriving upon a conclusion.
2 Social capital and economic well-being
Several features affect prosperity: structural factors such as infrastructure, transportation systems, or population structure; institutional factors like policies or governmental interventions; economic factors like capital, trade volume, or labour force (Acemoglu 2009, Barro, Sala-i Martin 2004, Kaldor 1957); additionally, social features such as individual human capital contribute to aggregate wealth (Barro 2001, Mankiw et al. 1992, Mincer 1984). Furthermore, social scientists are interested as to whether social relations affect wealth; social capital has proven to be a useful concept in the study of societal well-being (Newton 2001, Putnam, Helliwell 2004). Putnam (1993, 2000) argued in his seminal books that the more vital civil society, the better off the regional economy. He showed that a strong civil society, represented by the number of civic associations, is strongly related to both a prosperous economy and a working democracy.
2.1 The magical relationship between social capital and economic well-being
Putnam explained the relationship between civic associations and prosperity with “the magic of social capital” (Putnam 2000, p. 288). Generally speaking, networks of civic associations facilitate communication and coordination; they create an atmosphere of trust, enforce reputation, and can thereby solve dilemmas of collective action. Following rational choice theory, members of civic associations learn to cooperate and collaborate through regular meetings and durable networks because the opportunity for social control is high, and the incentives to defect are low (see Axelrod 2006). The “shadows of the future and of the past” are essential incentives that form a foundation for cooperation. Moreover, regular group interactions instil pro-social norms, habits of solidarity, and a feeling of common identity since the needs of the individual are subsumed under collective benefits (Almond, Verba 1963, Putnam 1993). These are side-effects of associational activities. Besides the basic functions associations permit such as playing baseball, singing in choral societies, or advocating for the deprived, social engagement makes them more trusting and better citizens. Such indirect effects of civic associations affect (more or less) all participants. Moreover, civic associations can directly support local economies, enlarge participants’ social networks and encourage networking between economic actors. Civic associations consume goods and services through their daily routine and thereby stimulate the economy. More than anything, they build trust and therefore responsibility in local economies. Even non-participants in some way related to those in the associations’ network, could directly or indirectly have access to its resources and contacts, learn social norms it promotes, and experience as well as carry on mutual trust. This is a process of diffusion using a transfer of trust, norms, and resources from the associational network into other parts of society – both private and public; this is a spillover effect of social capital. Putnam (2000, pp. 319-325) generalized this argumentation, and assumed that neighbourhoods, states and even nations benefit from their citizens’ social capital.1
2.2 Empirical studies on social capital and economic well-being
Inspired by Putnam’s assumption, researchers from different fields have analysed the impact of social capital on economic performance within and across spatial units. With the focus on the macro-level,2 Algan, Cahuc (2013) reviewed the international and interregional heterogeneity of trust as a measure of social capital, and found a strong relationship between trust and growth. Using an index of social capital, Doh, McNeely (2012) confirmed that social capital drives economic development in at least 47 countries. Regardless, aggregate economic well-being is composed of smaller spatial units’ performance; economic models for the state level, for instance, have to be translated into regional argumentation. Capello, Fratesi (2012) presented a newer version of their regional growth model. In line with Putnam’s tradition, they showed that regions exhibiting higher social capital cooperate better and grow faster. In related research, Fazio, Lavecchia (2013) found spatial heterogeneity in trust across European regions. They concluded that disaggregation at regional levels reveals information that remains elusive at the national level (Fazio, Lavecchia 2013, p. 315). In line with this conclusion, Iyer et al. (2005) suggested a shift towards a more region-specific approach to social capital.
According to the literature, social capital helps explain the success of regions: dense networks and embeddedness promote innovation and economic collaboration (Malecki 2012, Rutten, Boekema 2007). De Dominicis et al. (2013) studied the relationship of social capital and regional economic performance among 146 NUTS-2 regions across countries in Europe. Their spatial analyses showed that proximity and social capital matter for creating new knowledge and innovation. Similarly, Westlund, Adam (2010) analysed social capital and economic performance with a meta-analysis of 65 studies since 1995 at different spatial levels. 23 papers dealt with national analyses, 7 with regions over several countries, and 14 analyses concentrated on regions in one country.3 Most works use different social capital indicators like trust, membership, or indices. Only two of these studies (Rupasingha et al. 2000, Westlund, Calidoni-Lundberg 2007) analysed subnational regions in one country and the organisational density as a measure of social capital in a way that is congruent with this paper’s approach (see section 3). From a methodological perspective, these studies did not model spatial interdependence explicitly in their statistical analyses. Only three authors use dummy variables for the regions, fixed effects and/or clustered standard errors to correct for potential spatial clustering (Guiso et al. 2004, Miguel et al. 2005, Westlund, Calidoni-Lundberg 2007). However, Rupasingha et al. (2002) applied spatial regression models to analyse social capital and growth of per capita incomes. The spatial autoregressive and error models show that associational density, as a proxy for social capital, is positively associated with economic growth. The core of this study is whether this is the case for regions in Germany. Thus, the leading hypothesis is the higher the stock of social capital, the higher the regional economic well-being.
2.3 Spatial dimensions of social capital and economic well-being
Along the way of analysing the impact of social capital on economic well-being, the fact that the units of analysis are regions, demands attention in further analysis. As spatial units are likely to be interdependent, the assumption of statistical independence of observations in the ordinary regression context may be violated. In order to properly apply statistical analysis and to deduce correct interpretations, one must answer to what degree regions in Germany are dependent in space, but also how these spatial interdependencies look for social capital and economic well-being.
As it is reasonable to assume that regions can benefit from their geographical location, proximity to successful regions may help craft a region’s own performance, or contrary to that, unsuccessful regions may negatively influence their neighbours as well. Whether the mechanism that drives interdependencies is a contagion, diffusion or any other process: “near things are more related than distant things” (Tobler 1970) – the first law of geography (Tobler 1995, 2004). Although Westlund (2013) raises the argument that “the first law of geography has lost much of its importance and that many distant things nowadays are just as related as near things”, it is still relevant because proximity and locality are essential in deducing social capital (David et al. 2010, Glaeser et al. 2002) and economy, even in a globalised world (Cambridge Journal of Regions Economy and Society 2008, Combes et al. 2008, McKinnon, Cumbers 2014, Moretti 2012). Consequently, the outcomes of interdependence cluster in space and in that way differ between regions (Rutten et al. 2010). However, spatial analysis has especially been little connected to social capital so far, regardless of social capital maps having been published. For instance, Beugelsdijk, van Schaik (2005a,b) mapped the social capital’s dimensions trust and associations for the European regions (see also Fazio, Lavecchia 2013). While maps of social capital within a European country are also available (for instance, Italy: Buonanno et al. 2009, Crescenzi et al. 2013; Germany: Franzen, Botzen 2011; Switzerland: Franzen, Botzen 2014, Traunmueller et al. 2012), researchers have turned a blind eye to social capital’s spatial patterns. Whether space matters for social capital and economic well-being in Germany, and to what degree adjacent regions are more related than distant regions, is thereby part of this exploratory analysis. In addition to the leading hypothesis, this study investigates the spatial dimensions of social capital and economic well-being by formulating the following exploratory hypotheses: what exactly are the intricacies of spatial interdependencies of social capital and economic well-being in Germany, and what distance is crucial to the two variables of interest?
3 Measuring social capital and economic well-being in Germany
With the intent to operationalize social capital and economic well-being in line with Putnam’s studies, the spatial analysis uses two main data files. It combines an organisational survey representing social capital with regional socio-economic data from official German statistics. The independent variable of interest is the organisational density of voluntary associations – this indicates the stock of social capital. Generally, social capital can be deconstructed into cultural and structural aspects (van Deth 2003, among others). Norms and trust are within this cultural dimension, whereas networks are categorized as the structural aspect of social capital. Networks have been measured with multiple indicators, such as memberships, volunteering, or number of voluntary organisations. Albeit the measurement of social capital has sparked debate (Paldam 2000, Woolcock 2010), this work uses a solid and quantitative measurement, just as Putnam “… tried to measure social capital by counting groups in civil society” (Fukuyama 2001). The number of civic associations per 1000 inhabitants measures social capital in this case. Beside the work of Franzen, Botzen (2011) and Zimmer (2007) there has been little in the way of quantitative information on the scope of social capital in Germany, owing to the fact that all data on voluntary associations is stored locally, and partly handwritten, in federal courts; making a survey costly and time-consuming. In recent years, work has been in progress to ensure that information about Germany’s voluntary associations is standardized and accessible through the Statistical Business Register’s database. However, in 2012 the local registers still had to be contacted and the Statistical Business Register had to be consulted in order to carry out a complete inventory of all civic associations. The organisational census was conducted at the University of Bern in collaboration with the Stifterverband.4 Overall, the latest survey counted 580,294 voluntary organisations; on average, this was 7.21 civic associations per 1000 inhabitants. Furthermore, the Federal Statistical Office provides data on the regions’ socio-economic characteristics in its Regional Database Germany. The dependent variable is gross domestic product (GDP) per capita (from 2012) that operationalizes regional economic well-being.
The units of analysis in this study are 390 administrative districts in Germany.5 These sub-national units are called Landkreise (districts) and kreisfreie Städte (urban districts), subsumed under the nomenclature of territorial units for statistics 3 (NUTS-3 regions). They are the smallest regional units for which associational data can be collected and on which representative data on social capital was surveyed for the very first time. Unfortunately, the variable for social capital is therefore not available up until now for smaller areal units such as municipalities. Hence, districts and urban districts best represent the spatial areal unit to show a relationship between social capital and economic well-being. However, Raumordnungsregionen (ROR) – also called regional planning regions – may also be suitable for analysis as they are composed of functional regions based on economic dependence. But as they are large-area units (on average composed of four districts), the aggregation of districts can lead to artificial spatial patterns and bias the results of spatial analysis. This concern is known as the Modifiable Areal Unit Problem (Openshaw, Taylor 1979). This analysis chooses to deal with the districts instead of ROR because they are four-times more units of analysis as well as the smallest areal units for which data on organisational social capital is available and hence, a proper choice to reveal spatial phenomena.
4 Modelling spatial patterns in Germany
As distance and proximity respectively are substantial determinants for economic and social well-being of regions, modelling, detecting, and describing spatial patterns provide insights into social capital and economic well-being among Germany’s sub-national regions. The dependence among spatial units of analysis is commonly modelled by means of a connectivity matrix or weighting matrix. Generally, these matrices are N ×N big and describe how unit i is connected to unit j. A frequently used matrix is the nearest-neighbour matrix, which reflects adjacent units with 1 when they are neighbours or 1∕dij where dij is the distance between the neighbours, and 0 for not being a neighbour. Moreover, interdependence can be based on various mechanisms that drive the interrelations. Researchers can choose between geographical distance and substantive specification to model interdependence. Beck et al. (2006) argued that considering substantive information, such as trading partners in the analysis of the distribution of economy or use multiple spatial matrices in one analysis, might be useful as well (e.g. Hays et al. 2010). According to LeSage, Pace (2011), extending a spatial regression model with multiple matrices of different kinds of connectivity bears pitfalls. Considering this, but also due to the fact that substantive relations are costly to collect, the matrices used here are geographically weighted matrices using kilometres and units that share a border (see equations (1) and (2), which give examples and the corresponding spatially lagged dependent variable).
From an exploratory perspective, the focus lies on which geographic scope is characteristic
to regional economic well-being and social capital in Germany. Because closer things matter
more, the matrices are chosen in a way so that they represent different gradients of distances
with the objective of revealing the geographic scope that matters most to the variables of
interest. The first matrix represents the closest neighbours possible: those that share a border.
Therefore, 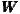 1 is a N × N binary matrix which codes wij = 1 for regions i and j that do
border and wij = 0 for regions that do not border (see equations (1) and (2)). The further
matrices increase the distance between regions stepwise in order to analyse spatial
patterns gradually. The following matrices are N × N connectivity matrices and reflect
neighbours by different distances dij. Distance is measured as kilometres between
the region i’s capital and the capital of the neighbouring region j; as explorations
have shown that capitals and urban districts play a major role in terms of regional
economic success. In each matrix
1 is a N × N binary matrix which codes wij = 1 for regions i and j that do
border and wij = 0 for regions that do not border (see equations (1) and (2)). The further
matrices increase the distance between regions stepwise in order to analyse spatial
patterns gradually. The following matrices are N × N connectivity matrices and reflect
neighbours by different distances dij. Distance is measured as kilometres between
the region i’s capital and the capital of the neighbouring region j; as explorations
have shown that capitals and urban districts play a major role in terms of regional
economic success. In each matrix 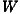 2-12, the distance dij is constrained by one of
the kilometre thresholds x:
2-12, the distance dij is constrained by one of
the kilometre thresholds x: 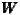 2: x=100 km,
2: x=100 km, 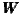 3: x=150 km,
3: x=150 km, 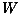 4: x=200 km,
4: x=200 km, 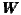 5:
x=250 km,
5:
x=250 km, 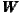 6: x=300 km,
6: x=300 km, 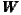 7: x=350 km,
7: x=350 km, 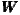 8: x=400 km,
8: x=400 km, 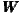 9: x=450 km,
9: x=450 km, 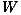 10:
x=500 km,
10:
x=500 km, 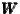 11: x=550 km, and
11: x=550 km, and 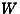 12: x=600 km, whereas the gradual increase of
each matrix’ radius may unveil the distance that matters most to social capital and
economic well-being. The maximum distance is equal to the width of Germany. If the
distance is greater than x-km radius, the weight equals 0. If the distance is equal or less
than the x-km radius, the weight is the inverse of the distance dij (see equation
(2)), so that the closer a region j is to unit i the larger the weight. Hence, each
element of the N × N matrix either codes wij = 0 or wij = 1∕dij (see equation
(2)).
12: x=600 km, whereas the gradual increase of
each matrix’ radius may unveil the distance that matters most to social capital and
economic well-being. The maximum distance is equal to the width of Germany. If the
distance is greater than x-km radius, the weight equals 0. If the distance is equal or less
than the x-km radius, the weight is the inverse of the distance dij (see equation
(2)), so that the closer a region j is to unit i the larger the weight. Hence, each
element of the N × N matrix either codes wij = 0 or wij = 1∕dij (see equation
(2)).
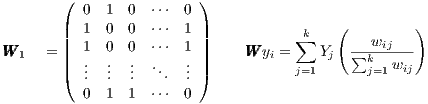 | (1) |
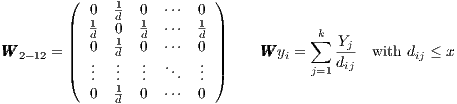 | (2) |
In the following analyses, all matrices 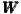 1-
1-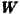 12 are row-standardised by dividing each cell
in a row by that row’s sum. These matrices are often referred to as row-stochastic, as their
elements sum up to one. Row-standardisation has the advantage that the spatial
lag has the same scale as the dependent variable y itself. But the normalisation
changes the relative weights of the proximal regions when the spatial matrix indicates
different numbers of neighbours. As more proximal units are considered, the weight of
neighbour jk becomes smaller. Thus, Pluemper, Neumayer (2010), as well as Ward,
Gleditsch (2008), argue that researchers should present substantive justification for
row-standardisation. In this example, the transformation is justified because the
economic influence of region j1 on region i might be smaller if there are several
other adjacent and competing regions jk-1, as compared to a case where region
i has only one or two neighbours which might have more influence on region i’s
economy.
12 are row-standardised by dividing each cell
in a row by that row’s sum. These matrices are often referred to as row-stochastic, as their
elements sum up to one. Row-standardisation has the advantage that the spatial
lag has the same scale as the dependent variable y itself. But the normalisation
changes the relative weights of the proximal regions when the spatial matrix indicates
different numbers of neighbours. As more proximal units are considered, the weight of
neighbour jk becomes smaller. Thus, Pluemper, Neumayer (2010), as well as Ward,
Gleditsch (2008), argue that researchers should present substantive justification for
row-standardisation. In this example, the transformation is justified because the
economic influence of region j1 on region i might be smaller if there are several
other adjacent and competing regions jk-1, as compared to a case where region
i has only one or two neighbours which might have more influence on region i’s
economy.
5 Exploratory spatial data analysis
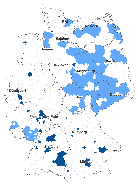
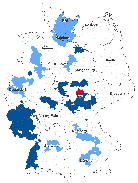
Generally, exploratory spatial data analysis (ESDA) tests whether spatial dependence is present in the data. The first simple tool to explore spatial patterns among Germany’s sub-national regions is a map of social capital and economic well-being. The maps presented here provide a general impression of the heterogeneous distribution of economic well-being (GDP per capita) and social capital (civic associations per 1,000 capita) among Germany’s districts. Figure 1 pictures such spatial patterns, where the darkest shade refers to the highest quintile. Both indicators heterogeneously spread over the country with a clear east-west decline in the distribution of economic well-being. Moreover, Germany’s urban districts exhibit higher GDP than its rural regions. On the other hand, social capital shows no clear east-west difference. Rather, there is what resembles a belt with a higher density of civic associations in the middle of the country. Additionally, in the north and the south, at the ends of the diagonal so to speak, there is a higher density of voluntary organisations.
 (a) Regional economic well-being
(a) Regional economic well-being  (b) Regional social capital
(b) Regional social capital
Spatial heterogeneity is clearly present in Germany’s regions in terms of economic
well-being and social capital. In order to explore it in more detail, diagnostic tests
for univariate spatial autocorrelation will analyse local and global spatial patterns
(Anselin 1995, Anselin et al. 1996, Getis 2007). Probably the most frequently used
spatial diagnostic tests are Local and Global Moran’s I that help to analyse spatial
patterns here. Global Moran’s I calculates the deviations of y from the mean, to
provide an (overall) correlation of an observation’s variable yi with those values
yj of the surrounding regions weighted by the spatial dependency wij given in the
matrix  . Moran’s I basically reflects the correlation of
. Moran’s I basically reflects the correlation of  y and y. Positive values
present patterns of similar values and negative coefficients indicate spatial clustering of
dissimilar values. The expected value of Moran’s I for no autocorrelation with a
standardised matrix is E[I] = -1∕(N - 1) (see Ward, Gleditsch 2008). So if the values of
Moran’s I are larger than this critical value (in this example -0.0025), global spatial
autocorrelation will be positive, whereas a smaller coefficient than the expected value will
indicate a negative spatial interdependence, given the p-value is >.05. The global
diagnostic reflects the overall spatial pattern in the data set depending on the spatial
weighting matrix, or in other words, on how the analysis employs and constructs
connectivity.
y and y. Positive values
present patterns of similar values and negative coefficients indicate spatial clustering of
dissimilar values. The expected value of Moran’s I for no autocorrelation with a
standardised matrix is E[I] = -1∕(N - 1) (see Ward, Gleditsch 2008). So if the values of
Moran’s I are larger than this critical value (in this example -0.0025), global spatial
autocorrelation will be positive, whereas a smaller coefficient than the expected value will
indicate a negative spatial interdependence, given the p-value is >.05. The global
diagnostic reflects the overall spatial pattern in the data set depending on the spatial
weighting matrix, or in other words, on how the analysis employs and constructs
connectivity.
Global Moran’s I for the variable economic well-being in Germany’s 390 regions shows
significant spatial association independently of the spatial pattern modelled in the matrices
(see Figure 2). The null hypothesis that the variables are randomly distributed in space can
therefore be rejected. However, matrices 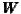 1 to
1 to 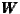 8, that reflect regions sharing a border and
those up to 400 km distant from one another, indicate positive autocorrelations; for example,
regions with higher GDP are surrounded by richer neighbours and regions with lower GDP the
opposite. But Global Moran’s I reveals a negative spatial association after exploring matrices
8, that reflect regions sharing a border and
those up to 400 km distant from one another, indicate positive autocorrelations; for example,
regions with higher GDP are surrounded by richer neighbours and regions with lower GDP the
opposite. But Global Moran’s I reveals a negative spatial association after exploring matrices
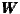 9 to
9 to 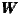 12, which consider regions weighted by the distances greater than a 450 km radius.
After widening the area under scrutiny, dissimilar clusters of regional GDP appear. This leads
to the conclusion that contagion has a certain distance threshold – at about 400
km.
12, which consider regions weighted by the distances greater than a 450 km radius.
After widening the area under scrutiny, dissimilar clusters of regional GDP appear. This leads
to the conclusion that contagion has a certain distance threshold – at about 400
km.
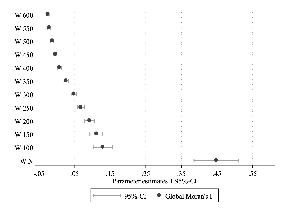
For the variable social capital, there is a significant positive global spatial association for
the six weighting matrices 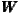 1 to
1 to 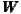 6, whereas the coefficient Global Moran’s I changes from
positive to negative if the distance threshold is beyond 250 km. In other words, regions with
similar social capital (either high or low) are closer to each other where ‘close’ means ‘within a
range of 250 km’. At distances beyond this threshold, social capital is negatively correlated in
space. Thus, the direction of the global measure’s sign for the variable social capital
changes earlier from positive to negative than for the variable economic well-being. To
summarize, the distance of regional clusters is fairly different for the stock of social capital
and economic well-being in Germany’s districts. Social capital appears as locally
rooted, whereas economic diffusion and contagion extend to a larger geographic
scope.
6, whereas the coefficient Global Moran’s I changes from
positive to negative if the distance threshold is beyond 250 km. In other words, regions with
similar social capital (either high or low) are closer to each other where ‘close’ means ‘within a
range of 250 km’. At distances beyond this threshold, social capital is negatively correlated in
space. Thus, the direction of the global measure’s sign for the variable social capital
changes earlier from positive to negative than for the variable economic well-being. To
summarize, the distance of regional clusters is fairly different for the stock of social capital
and economic well-being in Germany’s districts. Social capital appears as locally
rooted, whereas economic diffusion and contagion extend to a larger geographic
scope.
 (a) Global Moran’s I of economic well-being
(a) Global Moran’s I of economic well-being  (b) Global Moran’s I of social capital
(b) Global Moran’s I of social capital
Local Indicators of Spatial Association (LISA) are a decomposition of the global measure
(Anselin 1995, p. 97) and are defined as functions of a variable y observed at a region i and of
the values of that variable observed in the neighbourhood j. They test the null-hypothesis of
no spatial autocorrelation for each observation. One of the most common local indicators is
Local Moran’s Ii (Anselin 1995), which calculated the sub-regional deviations from a global
spatial autocorrelation measure and the squared differences in the variable of interest
in the neighbourhood respectively. This study calculates significant local spatial
accumulation of contrary or similar values for each region of analysis using the Local
Moran’s Ii for variables economic well-being and social capital. Exemplary for the
gradual increase of distance, Figure 3 represents significant spatial clusters for the
variable GDP and civic associations for the weighting matrices  1,
1, 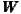 2,
2, 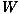 6, and
6, and 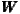 10.
The colouring discriminates between similar and dissimilar clusters of significant
spatial autocorrelation. Significant spatial autocorrelation is demonstrated by different
colors6 .
The light blue illustrates areas of low-low clusters (districts with low values surrounded by low
values), whereas the dark blue refers to high-high clusters (regions with high values
neighbouring high values). The red represents negative spatial autocorrelation, which are
spatial clusters of dissimilar values either low-high or high-low patterns. The maps show that
significant low-low clusters of economic well-being are concentrated in the east, whereas
significant clusters of high values are accumulated in the south. Despite the fact that spatial
patterns of social capital are more heterogeneous, one can notice significant clusters of high
values in the south-west and in the middle of Germany. Most importantly, Figure 3
demonstrates that the greater the distance modelled in the weighting matrix
10.
The colouring discriminates between similar and dissimilar clusters of significant
spatial autocorrelation. Significant spatial autocorrelation is demonstrated by different
colors6 .
The light blue illustrates areas of low-low clusters (districts with low values surrounded by low
values), whereas the dark blue refers to high-high clusters (regions with high values
neighbouring high values). The red represents negative spatial autocorrelation, which are
spatial clusters of dissimilar values either low-high or high-low patterns. The maps show that
significant low-low clusters of economic well-being are concentrated in the east, whereas
significant clusters of high values are accumulated in the south. Despite the fact that spatial
patterns of social capital are more heterogeneous, one can notice significant clusters of high
values in the south-west and in the middle of Germany. Most importantly, Figure 3
demonstrates that the greater the distance modelled in the weighting matrix 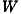 , the more
dissimilar the clusters. This supports the first law of geography that “near things are more
related than distant things”. In Germany, exploratory analysis has shown that different
distance thresholds affect spatial similarity. Local patterns of similar spatial dependencies are
found particularly for social capital. However, spatial patterns of economic well-being diffuse
wider.
, the more
dissimilar the clusters. This supports the first law of geography that “near things are more
related than distant things”. In Germany, exploratory analysis has shown that different
distance thresholds affect spatial similarity. Local patterns of similar spatial dependencies are
found particularly for social capital. However, spatial patterns of economic well-being diffuse
wider.
(a) Economic well-being
 (a) W1;N
(a) W1;N 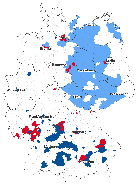 (b) W2;100km
(b) W2;100km 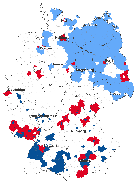 (c) W6;300km
(c) W6;300km 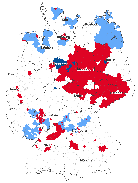 (d) W10;500km
(d) W10;500km
(b) Social capital
 (e) W1;N
(e) W1;N 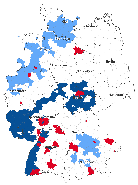 (f) W2;100km
(f) W2;100km 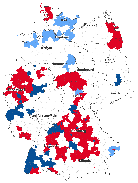 (g) W6;300km
(g) W6;300km 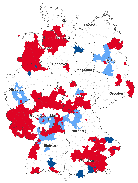 (h) W10;500km
(h) W10;500km

6 Spatial regression analysis
ESDA suggests that the data contains regional spatial clusters. This spatial interdependence must be considered in further statistical analyses on the well-being of regions in Germany. Interdependence violates the regression assumption that observations should be independent so that the errors are uncorrelated. Thus, ignoring significant spatial clustering in the error term of an OLS model potentially leads to biased standard errors and inefficient parameter estimates; while omitting spatial dependence as an explanatory variable may bias parameter estimates (LeSage, Pace 2009). In spatial econometrics, the spatial autoregressive lag and the spatial error model have so far been the most widely applied models to address spatial clustering in the data (Anselin 1988, Elhorst 2014, p. 9 for an overview). The researcher need only decide whether the correlation in space is substantial and can be modelled explicitly in a lag model (SAR), or if it is related to some unobserved variable and as a result should be built into the disturbances of the regression model (SEM) (see equations (3) and (4)).
Additionally, following Elhorst’s (2010, p. 16) recommended approach, statistical
diagnostics help strengthen the argumentation for (or against) a spatial regression model when
they identify if there is autocorrelation in the OLS-regression residuals (Anselin
et al. 1996, Buse 1982). This analysis conducts Moran’s I in combination with the classic and
robust Lagrange-Multiplier tests for spatial interdependence among the regression residuals so
as to show significant autocorrelation. The tests suggest that spatial interdependence should be
modelled in further statistical analysis but do not favour either model. Hence, a combination of
the lag and the error model might seem appealing. A linear combination of the SEM
and SAR respective data generating processes leads to the Spatial Durbin Model
(SDM) (LeSage, Pace 2009, p. 30f), which implements a spatially lagged dependent
variable 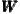 y as well as spatially lagged explanatory variables
y as well as spatially lagged explanatory variables 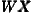 (see equation
(5)).
(see equation
(5)).
Researchers suggest one should prefer this model against others because its major virtue is the ability to generate unbiased coefficient estimates (Elhorst 2010, LeSage, Pace 2009, amongst others). This is the case regardless of the underlying spatial process. One might prefer an even more general model combining all three spatial components: a spatially lagged dependent variable, spatially lagged error term, and spatially lagged explanatory variables simultaneously; however, Elhorst (2010, p. 14) proved that one of the components has to be excluded in order to distinguish the spatial coefficients from each other and to meaningfully interpret them. As a result, SDM “is the best point of departure” (Elhorst 2010, p. 16, LeSage, Pace 2009, p. 46) for regression analysis.
6.1 Applied spatial regression analysis
Spatial regression analysis in this work studies whether social capital is a significant
determinant of economic well-being in Germany by foremost testing the relationship
between the regional density of civic associations as the indicator of social capital
(SC) and GDP (GDP). A series of control variables 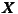 is also included (for details
on the variables see Table A.1 in the appendix). The first set of control variables
describes regional economic structure (unemployment rate, share of the tertiary
sector, number of welfare recipients), human capital (population with university
admission), and demographic variables such as the number of immigrants. The second set
of control variables additionally captures substantive spatial characteristics of the
districts, although spatial patterns are explicitly modelled in the weighting matrices.
Particularly, whether a region is, or has an urban district is important to consider
because they have a special legal status associated with socio-economic and political
characteristics. As Germany’s economic success depends on exports, a dummy variable
tries to capture diffusion process relationships with neighbouring countries taking 1
when a region borders another country. An additional dummy variable controls for
the fact that there are some units encompassing both types of districts (see section
3).
is also included (for details
on the variables see Table A.1 in the appendix). The first set of control variables
describes regional economic structure (unemployment rate, share of the tertiary
sector, number of welfare recipients), human capital (population with university
admission), and demographic variables such as the number of immigrants. The second set
of control variables additionally captures substantive spatial characteristics of the
districts, although spatial patterns are explicitly modelled in the weighting matrices.
Particularly, whether a region is, or has an urban district is important to consider
because they have a special legal status associated with socio-economic and political
characteristics. As Germany’s economic success depends on exports, a dummy variable
tries to capture diffusion process relationships with neighbouring countries taking 1
when a region borders another country. An additional dummy variable controls for
the fact that there are some units encompassing both types of districts (see section
3).
This work estimates different regression models. First, an Ordinary Least Square regression
model (OLS) functions here as a baseline for the other regression models. Second, as the SEM
and SAR regression models are commonly used in social science research as well as
previous spatial diagnostic tests justify both models’ use – this work estimates both
the SAR and SEM. Even so, it foremost applies the SDM because it is the only
model that generates unbiased coefficient estimates independent from the underlying
data-generating process. As mentioned, the different spatial regression models implement
different spatial lags in the equation. The SEM captures spatial interdependence
in the disturbance term, whereas the SAR and SDM model spatial relations as a
substantive variable (see equations (6), (7), (8)). This shows that regional GDP levels
depend on neighbouring regions’ GDP (ρ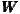 GDP). Moreover, the SDM implements the
spatial lag of the independent variable social capital (γ1
GDP). Moreover, the SDM implements the
spatial lag of the independent variable social capital (γ1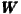 SC), and additionally
models that regional GDP relates to socio-economic determinants of spatial neighbours
(γ
SC), and additionally
models that regional GDP relates to socio-economic determinants of spatial neighbours
(γ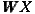 ). The spatial matrix
). The spatial matrix 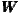 in all spatial regression models is
in all spatial regression models is 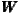 1 that represents
the neighbours that share a border, as it is the matrix with the strongest spatial
dependence (see Figure 2). Additionally, previous spatial regression analyses have
shown that matrix
1 that represents
the neighbours that share a border, as it is the matrix with the strongest spatial
dependence (see Figure 2). Additionally, previous spatial regression analyses have
shown that matrix  1 suits the data best, given the fit statistics of the models.
Nevertheless, social capital’s estimated effects on economic well-being will be presented
in section 6.2 for all spatial matrices that were introduced. This will provide an
overview of each matrix’ influence. This study’s spatial regression models are as
follows:
1 suits the data best, given the fit statistics of the models.
Nevertheless, social capital’s estimated effects on economic well-being will be presented
in section 6.2 for all spatial matrices that were introduced. This will provide an
overview of each matrix’ influence. This study’s spatial regression models are as
follows:
6.2 Spatial regression results
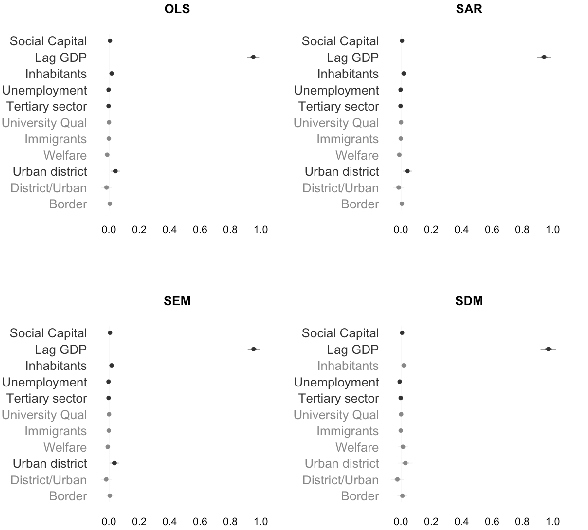
Table 1 and Figure 4 present the spatial regression models and, for the sake of comparability, the OLS model. Results support social capital research’s claim and this paper’s leading hypothesis: one additional association per 1,000 population corresponds to, on average, an almost 3 point increase in the regional GDP as represented by percentage. Moreover, regions with many inhabitants, lower unemployment rates, a high percentage of college graduates, and higher numbers of immigrants are economically better off, whereas a higher share of the tertiary sector correlates to a lower regional GDP. Bordering Germany’s neighbouring countries does not have a significant effect on regional economic well-being. Particularly, urban districts are more prosperous as they are associated with a GDP 35-percentage points higher than districts.
Concerning the spatial coefficients λ and ρ in the SAR, SEM and SDM, they reveal the gathering of positive spatial spillovers, where similar values tend to form spatial clusters among Germany’s regions. The spatial lag coefficient ρ of the SAR model (2) is significant and reflects neighbourhood clusters with positive spillovers, net of other factors. In addition to the positive spatial lag coefficient, the spatial error coefficient λ of the SEM model (3) shows significant positive spatial dependence in the residuals, which indicates determinants that contribute to the regional economic well-being in Germany, but remain absent in the regression model. Likewise, the model fit statistics show better fit for the spatial models than for the OLS. But as differences are not that big, spatial interdependency seems to be a rather minor determinant of economic well-being in Germany.
| (1) | (2) | (3) | |||||||||
| OLS | SAR | SEM | SDM | ||||||||
DV: GDP per capita (ln) | Estimate | Estimate | Estimate | Estimate | Lag
| ||||||
(Intercept) | 2. | 501*** | 2. | 017*** | 2. | 333*** | 2. | 229*** | |||
| (0. | 220) | (0. | 319) | (0. | 222) | (0. | 438) | ||||
Social Capital | 0. | 031*** | 0. | 031*** | 0. | 032*** | 0. | 026** | -0. | 015 | |
| (0. | 006) | (0. | 005) | (0. | 006) | (0. | 009) | (0. | 014) | ||
Socio-economic variables | |||||||||||
| Inhabitants (ln) | 0. | 074*** | 0. | 074*** | 0. | 088*** | 0. | 118*** | -0. | 114* | |
| (0. | 018) | (0. | 017) | (0. | 018) | (0. | 026) | (0. | 045) | ||
| Unemployment rate | -0. | 019*** | -0. | 017*** | -0. | 019*** | -0. | 023** | 0. | 015 | |
| (0. | 003) | (0. | 003) | (0. | 003) | (0. | 008) | (0. | 011) | ||
| Tertiary sector | -0. | 013*** | -0. | 012*** | -0. | 014*** | -0. | 014*** | 0. | 009** | |
| (0. | 001) | (0. | 001) | (0. | 001) | (0. | 002) | (0. | 003) | ||
| Qualification for university | 0. | 009*** | 0. | 008*** | 0. | 009*** | 0. | 011*** | -0. | 009** | |
| entrance | (0. | 001) | (0. | 001) | (0. | 001) | (0. | 002) | (0. | 003) | |
| Immigrants | 0. | 021*** | 0. | 017*** | 0. | 019*** | 0. | 021** | -0. | 005 | |
| (0. | 003) | (0. | 004) | (0. | 004) | (0. | 007) | (0. | 009) | ||
| Population on welfare | 0. | 037 | 0. | 040+ | 0. | 060* | 0. | 114** | -0. | 134* | |
| (0. | 025) | (0. | 024) | (0. | 027) | (0. | 042) | (0. | 059) | ||
Spatial variables | |||||||||||
| Urban district | 0. | 350*** | 0. | 337*** | 0. | 358*** | 0. | 369*** | -0. | 208+ | |
| (0. | 039) | (0. | 037) | (0. | 040) | (0. | 062) | (0. | 110) | ||
| District/urban district | 0. | 027 | 0. | 03 | 0. | 038 | 0. | 054 | -0. | 14 | |
| (0. | 050) | (0. | 047) | (0. | 047) | (0. | 057) | (0. | 130) | ||
| Border | -0. | 01 | -0. | 007 | -0. | 018 | -0. | 04 | 0. | 032 | |
| (0. | 027) | (0. | 025) | (0. | 029) | (0. | 043) | (0. | 063) | ||
Spatial Coefficients | |||||||||||
| ρ | 0. | 144+ | 0. | 350*** | |||||||
| (p-value) | 0. | 097 | 0. | 000 | |||||||
| λ | 0. | 419*** | |||||||||
| (p-value) | 0. | 000 | |||||||||
Model Fit | |||||||||||
| AIC | -174. | 027 | -174. | 783 | -195. | 374 | -194. | 198 | |||
| Log Likelihood | 99. | 012 | 100. | 392 | 110. | 687 | 120. | 099 | |||
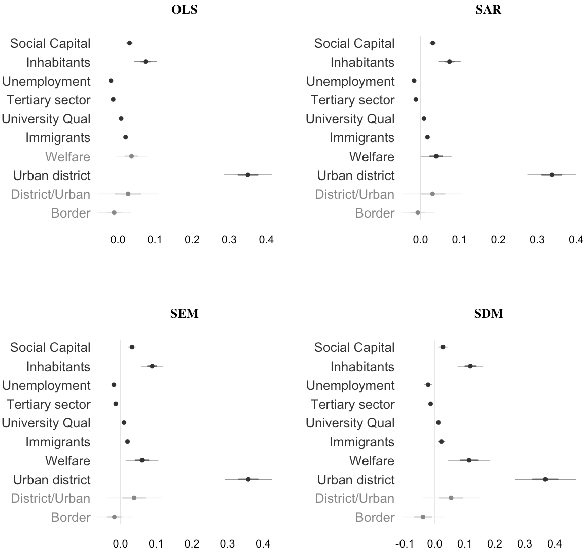 Note: Estimates with confidence intervals.
Note: Estimates with confidence intervals.
However, when dealing with spatial lags in regression models, the interpretation of
estimation results gets more complicated. For example, an increase in a variable in a region
may influence its well-being and potentially that in adjacent regions as well. In turn,
neighbouring regions may also influence this region. Particularly, the SDM models the
potential effects of region i affecting region j with the spatial lags of the dependent variable
 y and independent variables
y and independent variables  . However, the spatial lag estimation results of the SDM
cannot be interpreted directly, as the lag effects are decomposed in the change a region’s
experience within itself and a region’s own influence on its neighbours. The change that
directly affects another variable in a region is called a direct effect, whereas a change that
affects the variable in neighbouring regions is called an indirect effect. As these are cumulative
impacts, the sum of both effects estimates is called the total effect (LeSage, Pace 2009,
p. 33f).
. However, the spatial lag estimation results of the SDM
cannot be interpreted directly, as the lag effects are decomposed in the change a region’s
experience within itself and a region’s own influence on its neighbours. The change that
directly affects another variable in a region is called a direct effect, whereas a change that
affects the variable in neighbouring regions is called an indirect effect. As these are cumulative
impacts, the sum of both effects estimates is called the total effect (LeSage, Pace 2009,
p. 33f).
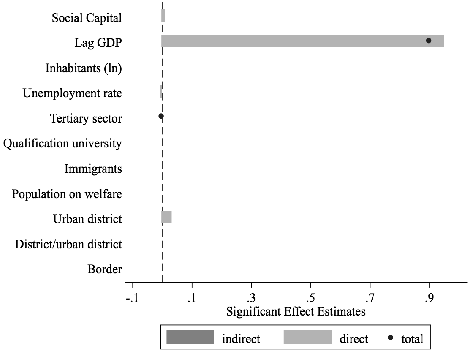
Concerning these effects estimates of social capital on economic well-being in Germany (see Table 2 and Figure 5), the estimation shows that a one-association increase per 1,000 inhabitants is related to roughly 2.4 percentage point increase in GDP within a region (direct effect). However, there is no significant indirect effect. Social capital’s effect is therefore local, as the direct effect is the only significant estimate. Overall, that the direct effects of explanatory variables within a district on economic well-being outgun the indirect effects on neighbours applies to all variables in the model (except qualification for university). Indeed, the economic well-being of a region heavily depends on its own socio-economic determinants and local characteristics, and less so on those of its neighbours.
| Variable | Direct Effects | Indirect Effects | Total
| ||||
| Social Capital | 0. | 024*** | -0. | 007 | 0. | 017 | |
| (0. | 000) | (0. | 488) | (0. | 171) | ||
| Inhabitants (ln) | 0. | 089*** | -0. | 082 | 0. | 007 | |
| (0. | 000) | (0. | 062) | (0. | 926) | ||
| Unemployment rate | -0. | 020*** | 0. | 007 | -0. | 013 | |
| (0. | 000) | (0. | 376) | (0. | 078) | ||
| Tertiary sector | -0. | 013*** | 0. | 004 | -0. | 008* | |
| (0. | 000) | (0. | 206) | (0. | 012) | ||
| Qualification for university | 0. | 009*** | -0. | 006* | 0. | 003 | |
| entrance | (0. | 000) | (0. | 041) | (0. | 376) | |
| Immigrants | 0. | 022*** | 0. | 003 | 0. | 025*** | |
| (0. | 000) | (0. | 756) | (0. | 000) | ||
| Population on welfare | 0. | 076* | -0. | 106 | -0. | 03 | |
| (0. | 013) | (0. | 051) | (0. | 589) | ||
| Urban district | 0. | 337*** | -0. | 089 | 0. | 248* | |
| (0. | 000) | (0. | 336) | (0. | 021) | ||
| District/urban district | 0. | 005 | -0. | 138 | -0. | 133 | |
| (0. | 942) | (0. | 385) | (0. | 462) | ||
| Border | -0. | 033 | 0. | 021 | -0. | 012 | |
| (0. | 297) | (0. | 655) | (0. | 916) | ||
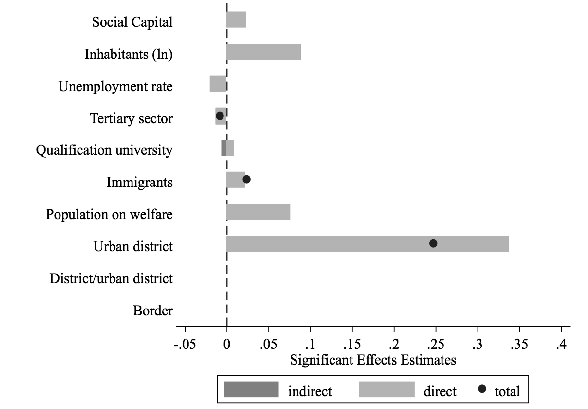
The strength of the impacts still depends on how the spatial connectivity is constructed by the spatial weight matrix. Figure 6 shows how social capital’s effects estimates depend on the spatial matrices. Nevertheless, effects estimates are robust to the choice of the spatial weight matrix; they are positive and significant across the alternative matrix specifications, supporting the local influence of social capital.
With respect to the substantive robustness of the regression results, modifications modelled whether the positive association between social capital and economic well-being is robust toward other spatial or socio-economic characteristics of the regions.7 The results show themselves as robust to the implementation of spatial dummy variables for the east or the north of Germany. In particular, the east is historically different from the rest of Germany but nevertheless insignificant in the pursuit of explaining regional well-being while controlling for spatial effects. Moreover, an additional dummy variable indicating metropolises (cities bigger than 500,000 inhabitants) has no influence on economic well-being. Whether the results are robust toward additional controls such as the age structure of the population, the total sex ratio, or for the population density was tested. None of these variables has a significant effect nor do they affect the positive relationship between social capital and economic well-being (see Franzen, Botzen 2011). To address the concern that important predictors were ignored, the preceding regression analyses in section 6.2 were re-estimated with the dependent variable lagged five years GDPt-5 to control for previous levels of GDP. This simultaneously controlled for determinants of economic well-being not originally included in the models but correlated with social capital and other significant explanatory variables. The results illustrate that social capital is still significant and positively associated with economic well-being, net of other control variables and of previous GDP-level (see Figures A.1 and A.2 in the appendix). If the analysis controls for the baseline GDPt-5, it yields results that more inhabitants, lower unemployment rate, and a weaker tertiary sector in a region as well as urban districts are still significant determinants and positively associated with higher regional GDP. Compared to previous regressions, economic well-being’s correlation with the share of the population with university admission, the rate of immigrants, and the share of welfare recipients diminishes completely (detailed Table A.2 in the appendix).
Moreover, spatial regression results of the explanatory variables are robust to the alternative specification of the weighting matrices. The choice of the spatial weights matrix affects only the spatial coefficient estimates of the spatially lagged variable and the error term. The direction of the explanatory variables’ association with economic well-being is also not affected by the matrix specification and the magnitude of the significant estimates only changes slightly. Particularly, social capital effects change only marginally and remain significant. As this paper aims to model spatial effects of regional (sub-national and sub-state level) economic well-being explicitly, it implements different alternatives of spatial dimensions in the weighting matrices. However, one could argue for state dummies to control for spatial patterns. But this proceeding would not allow for spatial effects across state borders and assume that regions of one state belong to the same cluster. In summary, independent of the regression modifications, the significant and positive relationship between social capital and the economic well-being in Germany’s regions remains the same.
6.3 Discussion
As this work is based on a finite sample of Germany’s districts and focuses on spatial interdependence within that country, the Boundary Value Problem confronts it (Anselin 1988). While it is well-known that Germany’s economic well-being depends heavily on trade with other countries, this analysis does not account for diffusion processes with regions outside the country’s borders. The dummy variable capturing the regions that border another country tries to mitigate this and work against the boundary value problem. This approach is nevertheless limited. This might be one reason for the unexplained dependencies in the spatial error model.
Furthermore, this study applies spatial exploratory and regression analysis, practically excluded in social capital research, but it suffers causal interpretation much like most studies with cross-sectional data. This analysis found a significant positive association between social capital and regional economic well-being as Putnam hypothesized. However, the current analysis does not allow causal inference from the presented results. A properly applied causal analysis would require panel data so as to draw the conclusion that social capital generates economic well-being. It may also be that the causal arrow is in reverse and that social capital is in fact rather a consequence of economic well-being. Even other types of causal analysis can just give additional hints rather than causal proofs without panel data analysis. Although minor studies have showed how propensity score analysis leads to the same findings, it merely provides an additional indication for the effect of social capital on prosperity. Nevertheless, extended hypothesis testing with organisational survey data from Switzerland supports the social capital effect of civic associations on regional economic well-being (Franzen, Botzen 2014). Yet, it could well be that further causal analysis cannot provide evidence that social capital causes economic well-being. However, this would not imply that the magic of social capital is illusive. The mechanisms that civic associations generate trust and facilitate cooperation can still be true, as research has shown (Botzen 2015, Claibourn, Martin 2000). Despite that, the causal path between social capital and its positive externalities such as economic well-being has to be analysed on the aggregate level in detail, although the causal mechanism is measureable at the individual level. Further analysis could thereby focus on the causal analysis and the mechanisms on the macro level; this would help examine whether the “magic of social capital” glows for spatial units.
Aside from the problem of causal inference, the measurement of social capital is also debateable. Despite the fact that the density of civic associations is a common measure of social capital, called “Putnam’s instrument” (Paldam, Svendsen 2000), this is a rather naive operational proxy. Were certain information available for Germany’s districts, deeper insight into the mechanism of social capital would have been possible. For instance, the type of the associations (e.g.: field of activity, bonding/bridging distinction), the number of memberships, or the members’ activity level might have been valuable statistics. Although some of this information is available for single cities or regions in Germany (Maloney et al. 2008, Zimmer 1992, 2007), a comprehensive nationwide survey of the districts has not so far been realized by the German government or a third party. Systematic quantitative data on social capital would allow properly detailed analyses of other indicators; this is definitely a research gap that must be dealt with in the near future. In addition, detailed data on social capital and its spatial patterns could help flourish interpretation of the exploratory results. Although this work’s explorations ascertain the geographic scope of social capital for the first time, the mechanisms behind the different thresholds remain undiscovered. Further data collection and analysis could shed light on why the geographic scope of social capital is smaller compared to the threshold of economic well-being.
Moreover, further research on regional social capital could extend the idea of the weighted matrices to other interdependencies. One might do this by modelling substantive relations between units of analysis such as expenditures for civil society, membership rates, and the share of volunteers in the population (e.g. Beck et al. (2006), as mentioned in section 3). Unfortunately, such substantive data for Germany’s administrative districts is not yet available. In addition to using substantive relations as interdependencies, one can extend the spatial model by using more than one weighted matrix. For instance, the multiple spatial models can capture different distances in the weighting matrix. However, these extensions themselves carry pitfalls noted by LeSage, Pace (2011). Nevertheless, methods of spatial econometrics are fruitful and flexible tools that will allow research to model, explore, and analyse interdependence, enriching analysis of social capital and regional well-being.
7 Conclusion
This work analysed Putnam’s idea that social capital shapes the economic well-being of subnational regions with Germany as its focus. It modelled, explored, and analysed spatial interdependence among 390 districts. Potential interdependence in space was captured by alternative specifications of weighting matrices that represent different geographic scopes and spillovers. Cross-sectional regression analysis applied three well-established spatial models and effects estimates.
Exploratory and regression analysis reveals that social capital and economic well-being are spatially clustered in Germany, compared to a random assignment. However, each variable’s radius of influence is different. Economic well-being has a larger sphere of spillovers, whereas the scope of social capital is rather regional. According to ESDA, the distance threshold of positive spatial correlation for economic well-being is at 450 km, while similar spatial patterns of social capital have a radius of less than 250 km. Likewise, effects estimates of the SDM reveal that only direct effects are significant. Accordingly, social capital is locally associated with economic well-being but has no effects on adjacent regions. Hence, this result underpins exploratory insights, suggesting social capital acts rather regionally. With regard to multivariate spatial analyses, the substantive interpretation of the regression models supports the social capital hypothesis, as the results show that associations matter for economic well-being, even as a macro-level variable. Regarding the specification of the spatial weighting matrices, regression results are robust to the alternatives. Foremost, the positive relationship between social capital and regional economic well-being remains the same. In sum, adequate spatial analysis of subnational German units supports Putnam’s hypothesis, that social capital is positively associated with the wealth of regions.
References
Acemoglu D (2009) Introduction to Modern Economic Growth. Princeton University Press, Princeton
Algan Y, Cahuc P (2013) Trust and growth. Annual Review of Economics 5: 521–549. CrossRef.
Almond GA, Verba S (1963) The Civic Culture: Political Attitudes and Democracy in Five Nations. Princeton University Press, Princeton
Anselin L (1988) Spatial Econometrics: Methods and Models. Kluwer Academic Publishers, Boston. CrossRef.
Anselin L (1995) Local indicators of spatial association – LISA. Geographical Analysis 27: 93–115. CrossRef.
Anselin L, Bera AK, Florax R, Yoon MJ (1996) Simple diagnostic tests for spatial dependence. Regional Science and Urban Economics 26: 77–104. CrossRef.
Axelrod RM (2006) The Evolution of Cooperation (revised ed.). Basic Books, New York
Barro RJ (2001) Human capital and growth. The American Economic Review 91: 12–17. CrossRef.
Barro RJ, Sala-i Martin X (2004) Economic Growth. MIT Press, Cambridge
Beck N, Gleditsch KS, Beardsley K (2006) Space is more than geography: Using spatial econometrics in the study of political economy. International Studies Quarterly 50: 27–44
Beugelsdijk S, van Schaik T (2005a) Differences in social capital between 54 Western European regions. Regional Studies 39: 1053–1064. CrossRef.
Beugelsdijk S, van Schaik T (2005b) Social capital and growth in European regions: An empirical test. European Journal of Political Economy 21: 301–324. CrossRef.
Bivand R, Piras G (2015) Comparing implementations of estimation methods for spatial econometrics. Journal of Statistical Software 63: 1–36. CrossRef.
Botzen K (2015) Are joiners trusters? a panel analysis of participation and generalized trust. Zeitschrift für Soziologie 44: 314–329
Boxman E, De Graaf P, Flap H (1991) The impact of social and human capital on the income attainment of Dutch managers. Social Networks 13: 51–73. CrossRef.
Buonanno P, Montolio D, Vanin P (2009) Does social capital reduce crime? Journal of Law & Economics 52: 145–170
Buse A (1982) The likelihood ratio, wald, and lagrange multiplier tests: An expository note. The American Statistician 36: 153–157. CrossRef.
Cambridge Journal of Regions Economy and Society (2008) The world is not flat; putting globalisation in its place. 1(3): 341-503
Capello R, Fratesi U (2012) Modelling regional growth: An advanced MASST model. Spatial Economic Analysis 7: 293–318. CrossRef.
Claibourn M, Martin P (2000) Trusting and joining? an empirical test of the reciprocal nature of social capital. Political Behavior 22: 267–291
Combes PP, Mayer T, Thisse JF (2008) Economic Geography: The Integration of Regions and Nations. Princeton
Cooke P, Clifton N, Oleaga M (2005) Social capital, firm embeddedness and regional development. Regional Studies 39: 1065–1077. CrossRef.
Crescenzi R, Gagliardi L, Percoco M (2013) Social capital and the innovative performance of Italian provinces. Environment and Planning A 45: 908–929. CrossRef.
David Q, Janiak A, Wasmer E (2010) Local social capital and geographical mobility. Journal of Urban Economics 68: 191–204. CrossRef.
De Dominicis L, Florax R, De Groot HL (2013) Regional clusters of innovative activity in Europe: Are social capital and geographical proximity key determinants? Applied Economics 45: 2325–2335. CrossRef.
Doh S, McNeely C (2012) A multi-dimensional perspective on social capital and economic development: An exploratory analysis. The Annals of Regional Science 49: 821–843
Elhorst JP (2010) Applied spatial econometrics: Raising the bar. Spatial Economic Analysis 5: 9–28. CrossRef.
Elhorst JP (Ed.) (2014) Spatial Econometrics: From Cross-Sectional Data to Spatial Panels. Springer-Verlag, Berlin
Fazio G, Lavecchia L (2013) Social capital formation across space: Proximity and trust in European regions. International Regional Science Review 36: 296–321. CrossRef.
Franzen A, Botzen K (2011) Vereine in Deutschland und ihr Beitrag zum Wohlstand der Regionen. Soziale Welt 62: 391–413. CrossRef.
Franzen A, Botzen K (2014) Mir hei e Verein: Ein Studie über Vereine, Sozialkapital und Wohlstand im Kanton Bern. Schweizerische Zeitschrift für Soziologie 40: 79–98
Franzen A, Hangartner D (2006) Social networks and labour market outcomes: The non-monetary benefits of social capital. European Sociological Review 22: 353–368. CrossRef.
Fukuyama F (2001) Social capital, civil society and development. Third World Quarterly 22: 7–20. CrossRef.
Gerber T, Mayorova O (2010) Getting personal: Networks and stratification in the Russian labor market, 1985-2011. American Journal of Sociology 116: 855–908. CrossRef.
Getis A (2007) Reflections on spatial autocorrelation. Regional Science and Urban Economics 37: 491–496. CrossRef.
Glaeser EL, Laibson D, Sacerdote B (2002) An economic approach to social capital. Economic Journal, 112(483): F437-F458
Graeff P (2009) Social capital: The dark side. In: Svendsen GT, Svendsen GLH (eds), Handbook of Social Capital. Edward Elgar Publishing, Cheltenham, 143–161. CrossRef.
Graeff P, Svendsen G (2013) Trust and corruption: The influence of positive and negative social capital on the economic development in the European Union. Quality and Quantity 47: 2829–2846. CrossRef.
Granovetter MS (1995) Getting a Job: A Study of Contacts and Careers. University of Chicago Press, Chicago
Guiso L, Sapienza P, Zingales L (2004) The role of social capital in financial development. The American Economic Review 94: 526–556. CrossRef.
Hays JC, Kachi A, Franzese RJ (2010) A spatial model incorporating dynamic, endogenous network interdependence: A political science application. Statistical Methodology 7: 406–428. CrossRef.
Iyer S, Kitson M, Toh B (2005) Social capital, economic growth and regional development. Regional Studies 39: 1015–1040. CrossRef.
Kaldor N (1957) A model of economic growth. The Economic Journal 67: 591–624. CrossRef.
Kwon SW, Heflin C, Ruef M (2013) Community social capital and entrepreneurship. American Sociological Review 78: 980–1008. CrossRef.
Lancee B (2010) The economic returns of immigrants’ bonding and bridging social capital: The case of the Netherlands. The International Migration Review 44: 202–226. CrossRef.
Lancee B (2012) The economic returns of bonding and bridging social capital for immigrant men in Germany. Ethnic and Racial Studies 35: 664–683. CrossRef.
Lee R (2009) Social capital and business and management: Setting a research agenda. International Journal of Management Reviews 11: 247–273. CrossRef.
LeSage J, Pace RK (2009) Introduction to Spatial Econometrics. CRC Press Taylor & Francis, Boca Raton. CrossRef.
LeSage JP, Pace RK (2011) Pitfalls in higher order model extensions of basic spatial regression methodology. The Review of Regional Studies 41: 13–26
Malecki E (2012) Regional social capital: Why it matters. Regional Studies 46: 1023–1039. CrossRef.
Maloney WA, Deth JWv, Rossteutscher S (2008) Civic orientations: Does associational type matter? Political Studies 56: 261–287. CrossRef.
Mankiw NG, Romer D, Weil DN (1992) A contribution to the empirics of economic growth. The Quarterly Journal of Economics 107: 407–437. CrossRef.
McKinnon D, Cumbers AD (2014) Introduction to Economic Geography: Globalization, Uneven Development and Place. Taylor & Francis, London
Miguel E, Gertler P, Levine DI (2005) Does social capital promote industrialization? Evidence from a rapid industrializer. The Review of Economics and Statistics 87: 754–762
Mincer J (1984) Human capital and economic growth. Economics of Education Review 3: 195–205. CrossRef.
Moretti E (2012) The New Geography of Jobs. Houghton Mifflin Harcourt, New York
Mouw T (2003) Social capital and finding a job: Do contacts matter? American Sociological Review 68: 868–98. CrossRef.
Newton K (2001) Trust, social capital, civil society, and democracy. International Political Science Review 22: 201–14. CrossRef.
Obukhova E, Lan G (2013) Do job seekers benefit from contacts? A direct test with contemporaneous searches. Management Science 59: 2204–2216
Openshaw S, Taylor P (1979) A million or so correlation coefficients: Three experiments on the modifiable areal unit problem. Statistical Applications in the Spatial Sciences 21: 127–144
Paldam M (2000) Social capital: One or many? Definition and measurement. Journal of Economic Surveys 14: 629–653
Paldam M, Svendsen GT (2000) An essay on social capital: Looking for the fire behind the smoke. European Journal of Political Economy 16: 339–366. CrossRef.
Pluemper T, Neumayer E (2010) Model specification in the analysis of spatial dependence. European Journal of Political Research 49: 418–442. CrossRef.
Putnam RD (1993) Making Democracy Work: Civic Traditions in Modern Italy. Princeton University Press, Princeton, NJ
Putnam RD (2000) Bowling Alone. The Collapse and Revival of American Community. Simon & Schuster, New York
Putnam RD, Helliwell JF (2004) The social context of well-being. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences 359: 1435–1446. CrossRef.
Rupasingha A, Goetz SJ, Freshwater D (2000) Social capital and economic growth: A county-level analysis. Journal of Agricultural and Applied Economics 32: 565–572
Rupasingha A, Goetz SJ, Freshwater D (2002) Social and institutional factors as determinants of economic growth: Evidence from the United States counties. Papers in Regional Science 81: 139–155. CrossRef.
Rutten R, Boekema F (2007) Regional social capital: Embeddedness, innovation networks and regional economic development. Technological Forecasting & Social Change 74: 1834–1846
Rutten R, Westlund H, Boekema F (2010) The spatial dimension of social capital. European Planning Studies 18: 863–871. CrossRef.
Thompson J (2005) Proactive personality and job performance: A social capital perspective. Journal of Applied Psychology 90: 1011–1017. CrossRef.
Tobler WR (1970) Computer movie simulating urban growth in the Detroit region. Economic Geography 46: 234–240. CrossRef.
Tobler WR (1995) Migration: Ravenstein, Thornthwaite, and beyond. Urban Geography 16: 327–343. CrossRef.
Tobler WR (2004) On the first law of geography: A reply. Annals of the Association of American Geographers 94: 304–310. CrossRef.
Traunmueller R, Stadelmann-Steffen I, Ackermann K, Freitag M (2012) Zivilgesellschaft in der Schweiz: Analysen zum Vereinsengagement auf lokaler Ebene. Seismo, Zürich
Tsai WP, Ghoshal S (1998) Social capital and value creation: The role of intrafirm networks. Academy of Management Journal 41: 464–476. CrossRef.
van Deth JW (2003) Measuring social capital: Orthodoxies and continuing controversies. International Journal of Social Research Methodology 6: 79–92. CrossRef.
Ward MD, Gleditsch KS (2008) Spatial Regression Models. Sage Publications, Los Angeles
Westlund H (2013) A brief history of time, space, and growth: Waldo Tobler’s first law of geography revisited. The Annals of Regional Science 51: 917–924
Westlund H, Adam F (2010) Social capital and economic performance: A meta-analysis of 65 studies. European Planning Studies 18: 893–919. CrossRef.
Westlund H, Calidoni-Lundberg F (2007) The creative class and social capital – civil society, regional development and high-tech employment in japan. Royal institute of technology, cesis - centre of excellence for science and innovation studies, stockholm
Woolcock M (2010) The rise and routinization of social capital, 1988-2008. Annual Review of Political Science 13: 469–487. CrossRef.
Zimmer A (1992) Vereine heute – zwischen Tradition und Innovation. Ein Beitrag zur Dritten-Sektor-Forschung. Birkhäuser, Basel
Zimmer A (2007) Vereine – Zivilgesellschaft konkret. VS Verlag für Sozialwissenschaften, Wiesbaden. CrossRef.
A Appendix
| Variable | Measurement | Mean | Std.Dev. | Min | Max | Origin |
| Social Capital | associations per | 7.365 | 1.840 | 3.583 | 13.019 | Survey |
| 1000 capita | ||||||
| GDP (ln) | GDP per capita in | 3.438 | 0.327 | 2.772 | 4.789 | |
| 1000€(ln) | ||||||
| Urban district | dummy, Yes =1 | 0.249 | 0.433 | 0 | 1 | |
| District/urban district | dummy, Yes =1 | 0.044 | 0.204 | 0 | 1 | |
| Border | dummy, Yes =1 | 0.167 | 0.373 | 0 | 1 | |
| Inhabitants (ln) | number of inhabitants | 11.998 | 0.661 | 10.43 | 15.062 | |
| (ln) | ||||||
| Unemployment rate | % of unemployed in | 7.436 | 4.35 | 1.6 | 57.856 | Regional |
| population | Database | |||||
| Tertiary sector | % of tertiary sector of | 50.028 | 8.403 | 22.701 | 74.904 | Germany |
| GVA | ||||||
| Qualification | % of pupils with | 34.415 | 8.911 | 13.061 | 62.588 | |
| university | ”Abitur” (qualification | |||||
| for university entrance) | ||||||
| of all graduated pupils | ||||||
| Immigrants | % of immigrants in | 7.448 | 4.449 | 0.795 | 26.771 | |
| population | ||||||
| Population on welfare | % of welfare recipients | 1.328 | 0.504 | 0.332 | 3.349 | |
| in population | ||||||
| (1) | (2) | (3) | (4) | ||||||||
DV: GDP per Capital | OLS | SAR | SEM | SDM | |||||||
(ln) | Estimate | Estimate | Estimate | Estimate | Lag
| ||||||
(Intercept) | 0. | 188+ | 0. | 132 | 0. | 164 | 0. | 454* | |||
| (0. | 109) | (0. | 155) | (0. | 109) | (0. | 201) | ||||
Social Capital | 0. | 006* | 0. | 006** | 0. | 007* | 0. | 007+ | -0. | 006 | |
| (0. | 002) | (0. | 002) | (0. | 003) | (0. | 004) | (0. | 006) | ||
GDP (ln) 2008 | 0. | 949*** | 0. | 942*** | 0. | 953*** | 0. | 970*** | -0. | 374*** | |
| (0. | 023) | (0. | 027) | (0. | 023) | (0. | 030) | (0. | 090) | ||
Socio-economic variables | |||||||||||
| Inhabitants (ln) | 0. | 017* | 0. | 018* | 0. | 017* | 0. | 018 | -0. | 020 | |
| (0. | 008) | (0. | 008) | (0. | 008) | (0. | 012) | (0. | 02) | ||
| Unemployment rate | -0. | 003+ | -0. | 002+ | -0. | 003* | -0. | 008* | 0. | 009+ | |
| (0. | 001) | (0. | 001) | (0. | 001) | (0. | 004) | (0. | 005) | ||
| Tertiary sector | -0. | 003*** | -0. | 003*** | -0. | 002*** | -0. | 002* | 0. | 000 | |
| (0. | 001) | (0. | 001) | (0. | 001) | (0. | 001) | (0. | 001) | ||
| Qualification for university | 0. | 000 | 0. | 000 | 0. | 000 | 0. | 001 | -0. | 002 | |
| entrance | (0. | 001) | (0. | 001) | (0. | 001) | (0. | 001) | (0. | 001) | |
| Immigrants | -0. | 001 | -0. | 001 | -0. | 001 | -0. | 001 | 0. | 004 | |
| (0. | 002) | (0. | 002) | (0. | 002) | (0. | 003) | (0. | 004) | ||
| Population on welfare | -0. | 012 | -0. | 011 | -0. | 008 | 0. | 013 | -0. | 032 | |
| (0. | 011) | (0. | 011) | (0. | 012) | (0. | 019) | (0. | 026) | ||
Spatial variables | |||||||||||
| Urban district | 0. | 041* | 0. | 042* | 0. | 036+ | 0. | 029 | -0. | 004 | |
| (0. | 018) | (0. | 018) | (0. | 019) | (0. | 029) | (0. | 049) | ||
| District/urban district | -0. | 016 | -0. | 016 | -0. | 019 | -0. | 024 | 0. | 010 | |
| (0. | 021) | (0. | 021) | (0. | 02) | (0. | 025) | (0. | 057) | ||
| Border | 0. | 005 | 0. | 006 | 0. | 005 | 0. | 009 | -0. | 008 | |
| (0. | 011) | (0. | 011) | (0. | 012) | (0. | 019) | (0. | 027) | ||
Spatial Coefficients | |||||||||||
| ρ | 0. | 022 | 0. | 336*** | |||||||
| (p-value) | 0. | 63 | 0. | 000 | |||||||
| λ | 0. | 352*** | |||||||||
| (p-value) | 0. | 000 | |||||||||
Model Fit | |||||||||||
| AIC (Linear model) | -839. | 902 | -838. | 13 | -852. | 85 | -840. | 85 | |||
| Log Likelihood | 432. | 951 | 433. | 07 | 440. | 42 | 445. | 42 | |||