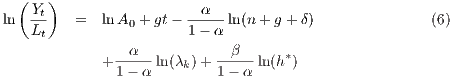Volume
5, Number 3, 2018, 75–96 journal homepage:
region.ersa.org
Volume
5, Number 3, 2018, 75–96 journal homepage:
region.ersa.orgDOI: 10.18335/region.v5i3.155
Regional dynamics of economic performance in the EU: To what extent do spatial spillovers matter?
1 Agence Française de Développement, Paris, France2 Banque de France, Paris, France Received: 1 September 2016/Accepted: 10 November 2018
Abstract. This paper investigates the main determinants of economic performance in the EU from a regional perspective, covering 253 regions over the period 2001-2008. In addition to the traditional determinants of economic performance, measured by GDP per capita, the analysis accounts for spatial effects related to externalities from neighbouring regions. The spatial Durbin random-effect panel specification captures spatial feedback effects from neighbouring regions through spatially lagged dependent and independent variables. The social-economic environment and traditional determinants of GDP per capita (distance from innovation frontier, physical as well as human capital and innovation) are found to be significant. Overall, our findings confirm the significance of spatial spillovers, as business investment and human capital of neighbouring regions have a positive impact – both direct and indirect – on economic performance of a given region.
JEL classification: 017, 031, 018, R12
Key words: Spatial Durbin Models, spatial spillovers, economic performance
1 Introduction
The declining trend in potential growth in most advanced economies started well before the Global Financial Crisis and the debate on ‘secular stagnation’ has gained further importance recently1 . The evidence is even stronger in Europe where not only potential growth has gradually declined over the past decades, but also the trend of output per capita has been lagging behind the United States. In the literature, weaker growth in Europe is explained to a large extent by productivity differences, in turn related to the lag in technological diffusion. Given the heterogeneity in Europe, not only across countries but also across regions, understanding the process of growth and innovation requires taking spatial dynamics into account. Notably, spatial spillovers may matter to explain concentration effects, agglomeration economies and industry clusters.
In 2010 the European Commission launched a strategy – “Europe 2020” – to “deliver smart, sustainable and inclusive growth” (European Commission 2010a). The European regional policy finds its the origins in the Treaty of Rome, which founded the European Economic Community in 1947. The strategy designed in 2010 aims at reforming regional policy to encourage measures to “unlock the growth potential of the EU by promoting innovation in all regions (…) by creating favourable conditions for innovation, education and research thereby encouraging R&D and knowledge-intensive investment and move towards higher value added activities” (European Commission 2010b). Overall, such policies aim at fostering market integration within Europe, while alleviating regional fragmentation. With a more integrated European market, economic growth in one region enlarges the market capacity and stimulates the mobility of factors of production and the process of innovation diffusion.
The knowledge and innovation capacity of the European regions depends on many factors including education, the availability of a skilled labour force and R&D intensity. However, it appears that performance in R&D and innovation varies markedly across EU regions (European Commission 2010b) (see Figure 1). The way innovation affects economic performance in traditional economic models has been recently questioned by empirical analyses. Indeed, the diffusion of innovation appears more complex than the traditional linear innovation model, whereby research leads to innovation, in turn creating economic growth (Bush 1945, Maclaurin 1953). These linear approaches have been challenged by recent empirical work considering research and innovation together with social and structural conditions in each region (Rodriguez-Pose, Crescenzi 2008, Usai 2011). The diffusion of innovation also depends on cross-regional spillovers and recent empirical analyses departs from pure knowledge spillovers (as in Jaffe et al. 1993) to also consider socioeconomic spillovers (as in Crescenzi et al. 2007).
Unlike our research question, most of the empirical studies focus on specific aspects of regional growth heterogeneity. For instance, some contributions focus on the link between technological innovation and regional growth (Evangelista et al. 2018), on the role of transport infrastructure endowment (Crescenzi, Rodriguez-Pose 2012) or the quality of financial institutions as determinants of regional growth (Hasan et al. 2009).
Two papers, like this paper’s research focus, study the determinants of economic performance at the EU regional level from a broader perspective. First, Rodriguez-Pose, Crescenzi (2008) combine R&D, spillovers, and innovation systems approaches in one model through a multiple regression analysis conducted for all regions of the EU-25. They included measures of R&D investment, proxies for regional innovation systems, and knowledge and socio-economic spillovers. The authors find significant contributions of innovation and innovation spillovers across regions to economic performance, but do not find any significant impact of long-term unemployment levels. Secondly, Wagner, Zeileis (2017) assess heterogeneity of growth and convergence processes based on economic growth regressions for 255 EU NUTS2 regions from 1995-2005. The starting point of the analysis is a human-capital-augmented Solow-type growth equation. Spatial dependencies are taken into account by augmenting the OLS regressions with a spatial lag. Initial GDP and the share of the working age population with high education significantly explains economic development. However, they find that the investment share in physical capital is only significant for coastal regions in the EU peripheral countries. Finally, although accounting for spatial dependencies changes the estimated coefficients, regional spillovers remain very small in their study.
This paper brings new evidence to the recent literature by investigating the main determinants of economic performance, measured by GDP per capita, in the EU from a regional perspective. In addition to the traditional determinants (such as investment, human capital development and innovation), our analysis accounts for spatial effects related to externalities from neighbouring regions. As in previous research, we develop specifications for economic performance depending on three main factors : internal innovative efforts, local socio-economic factors conducive to innovation and spatially-bound knowledge spillovers. Compared to existing work, the value added of our research is twofold. First, we take advantage of granular information by using a new database, the European Cluster Observatory dataset, covering 253 EU regions in 2001-2008 including new variables on innovation, physical and human capital. To our knowledge, no available studies use the dataset for similar purposes, wherein lies the originality of our contribution. Second, we exploit both the spatial and temporal dimensions of the dataset through the estimation of a spatial Durbin random-effect panel model, which captures spatial feedback effects from neighbouring regions through spatially lagged dependent and independent variables.
Our results show that the social-economic environment and traditional determinants (e.g. initial economic conditions, investment, human capital) have a significant impact on economic performance. Overall, our findings confirm the existence of significant spatial spillovers. In addition, business investment and human capital in the neighbouring regions are found to have a positive impact – both direct and indirect – on economic performance of a given region.
The paper is organised as follows : Section 2 presents the dataset and some derived stylised facts which will be explained by the empirical work. Section 3 gives the empirical specification used in this paper and the econometric approach followed to estimate it. Section 4 presents the empirical results and compares them with the existing literature. Section 5 concludes.
2 Dataset and stylised facts
2.1 The European Cluster Observatory dataset
The data used in this research comes from the European Cluster Observatory, an initiative of the European Commission in the context of the Europe 2020 strategy, which provides statistical information and analyses on clusters in Europe. The concept of clusters, first introduced by Porter (1990), refers to the ”regional concentration of economic activities in related industries, connected through multiple types of linkages” (Ketels, Protsiv 2014), which support the development of new competitive advantages in emerging industries. Cluster policies are part of the Europe 2020 strategy to rejuvenate EU’s industry. In this context, the European Cluster Observatory provides an EU-wide comparative cluster mapping with sectoral and cross-sectoral statistical analysis of the geographical concentration of economic activities and performance. The associated dataset covers a large range of series on economic performance (GDP per capita, GDP growth, productivity) as well as on its different drivers, including investment, employment, skills, education, R&D and innovation. The time series are available at the NUTS 2 level for the EU over the period 2001-2008.
Although the period covered may appear outdated, we justify its use for two main reasons. First, the European Cluster Observatory dataset is an exclusive database and the information details make this data unique and useful for research purposes. Indeed, compared to alternative European regional datasets (like Eurostat’s regional statistics), the dataset used in this paper includes broader and more detailed information on a regions’ business environment, such as labour quality, research and education, and access to venture capital and advanced infrastructure. The variables useful for our empirical analysis include in particular business investment (whereas Eurostat regional statistics mix public and private investment), skilled migrants and long-term unemployment. Such variables are key determinants of economic performance and are exclusively included in the European Cluster Observatory dataset. Second, working with pre-2008 financial crisis data makes the empirical work more stable and more meaningful to study long-term issues such as trend growth or convergence.
 (a) Business investment
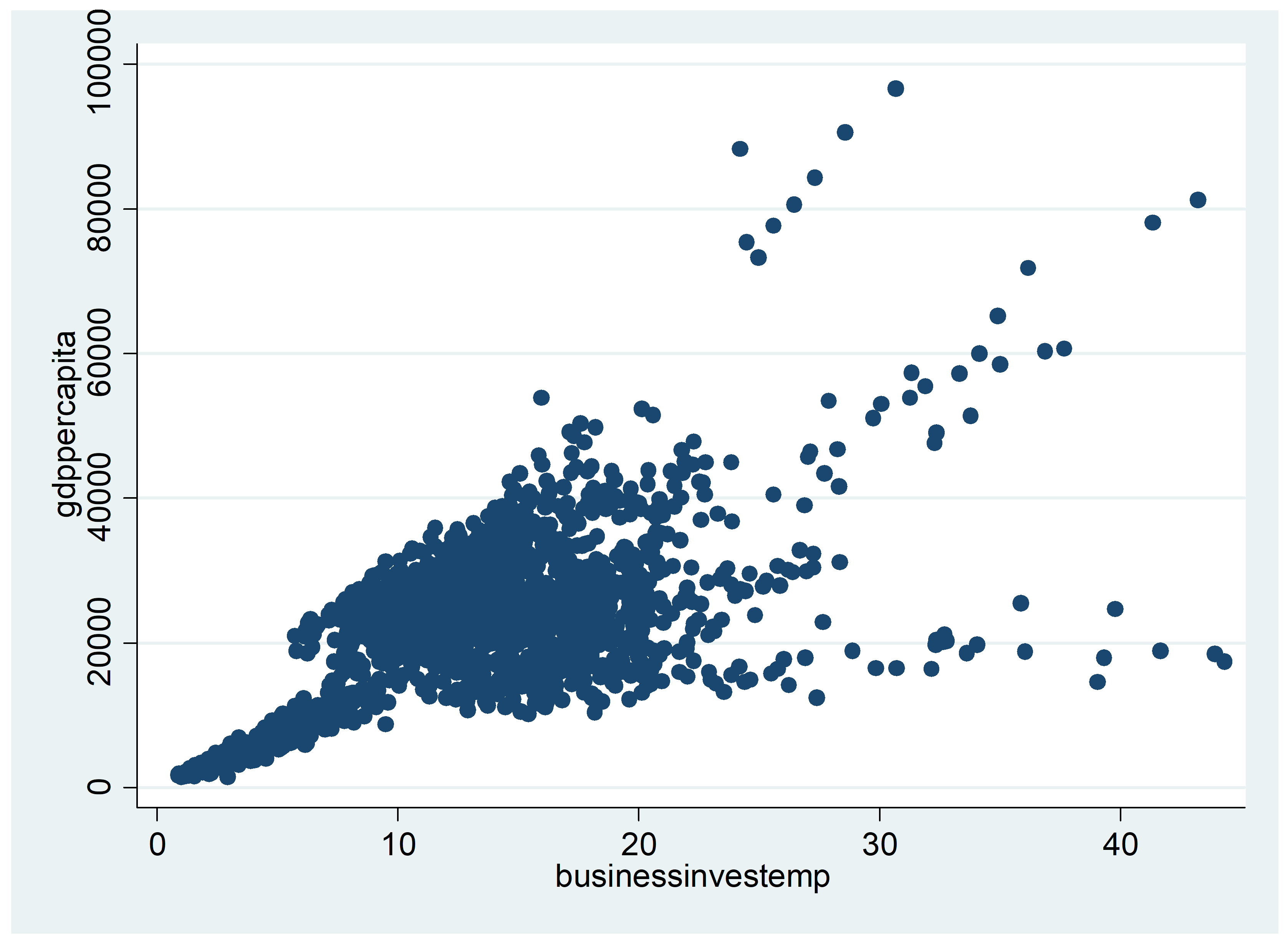
(a) Business investment 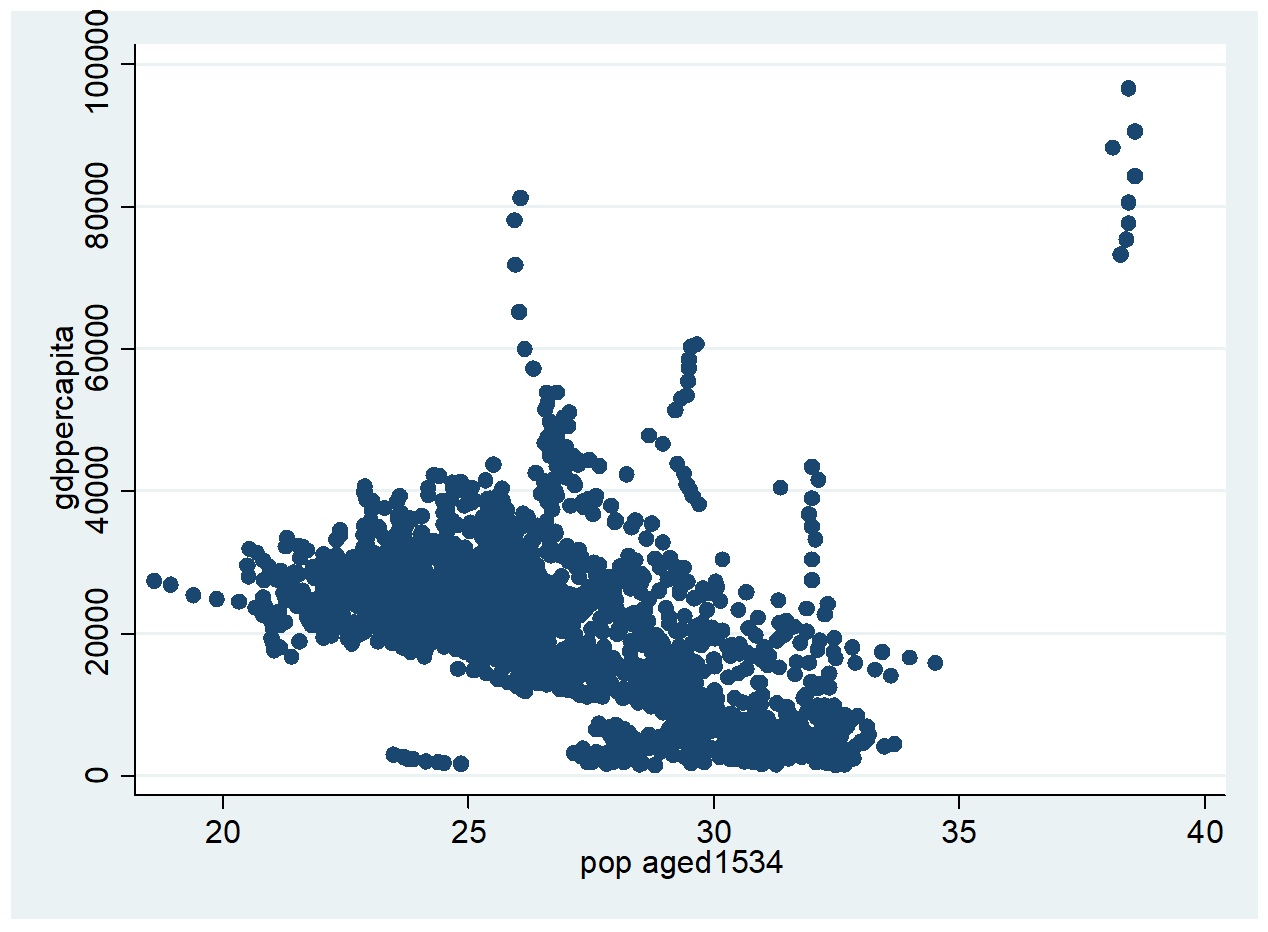 (b) Population aged 15-34
(b) Population aged 15-34  (c) Tertiary education
(c) Tertiary education
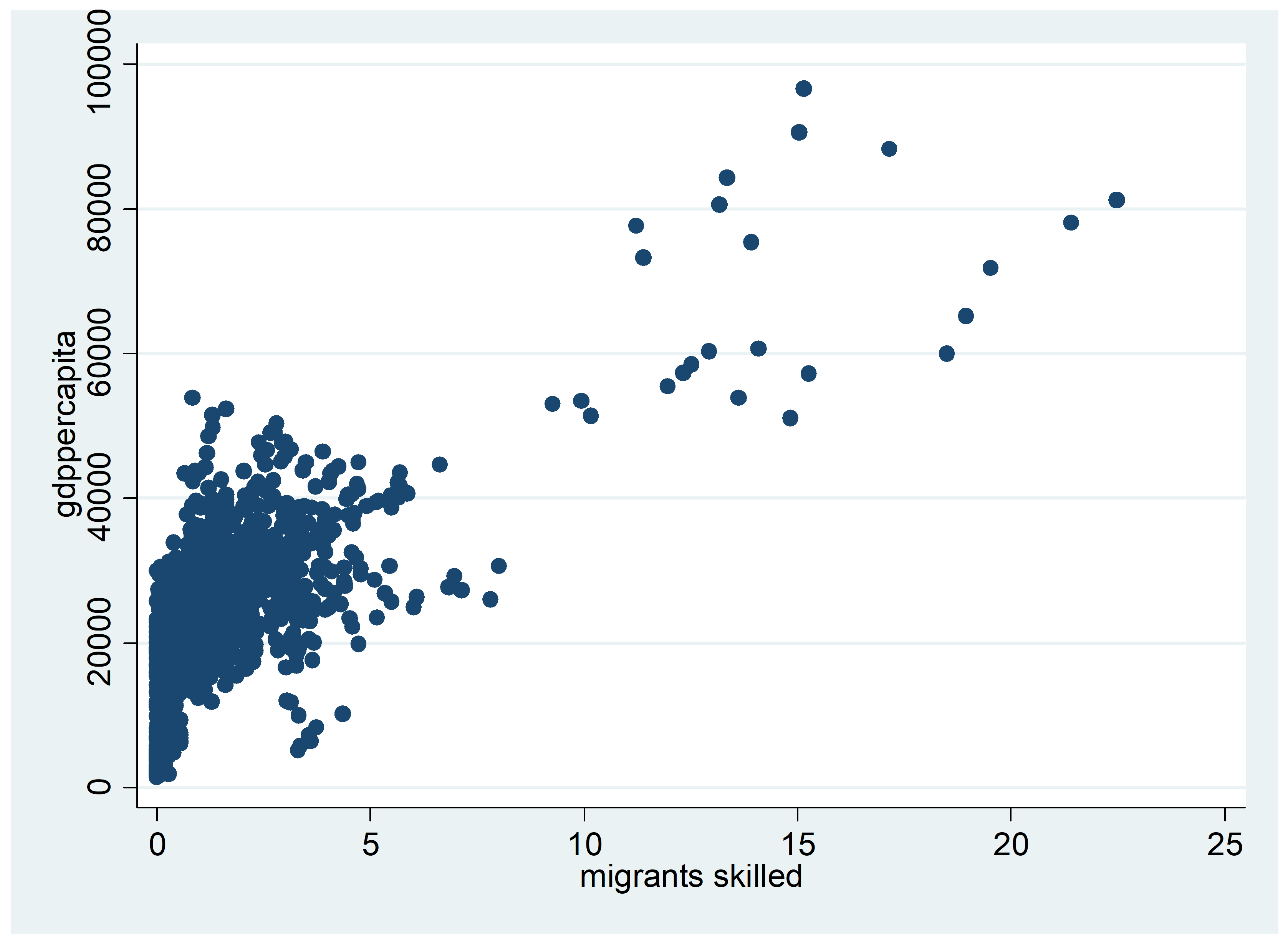 (d) Skilled migrants
(d) Skilled migrants 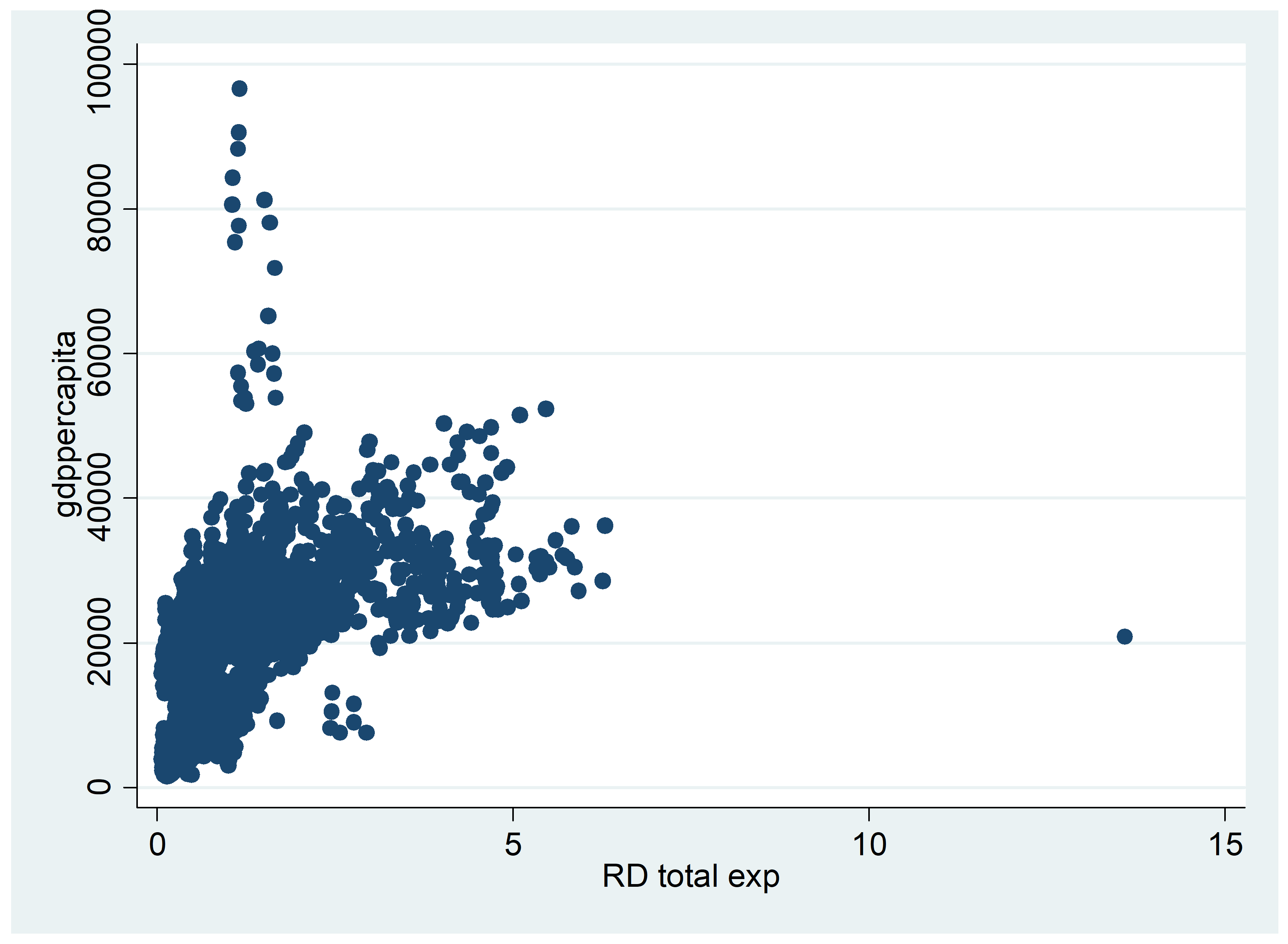 (e) R%D public exp. (% of GDP)
(e) R%D public exp. (% of GDP) 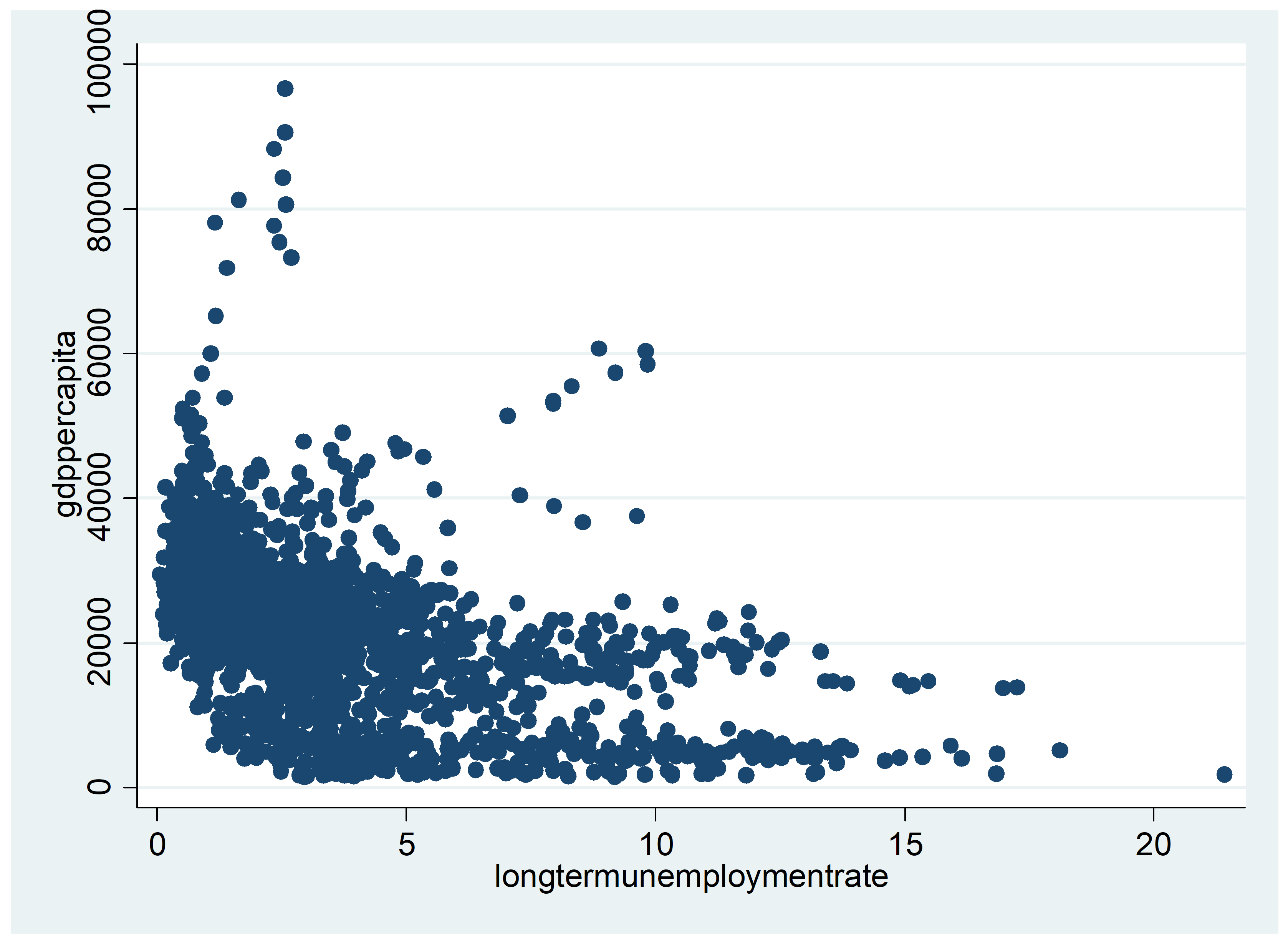 (f) Long-term unemployment
(f) Long-term unemployment
2.2 Stylised facts on economic performance at the European regional level
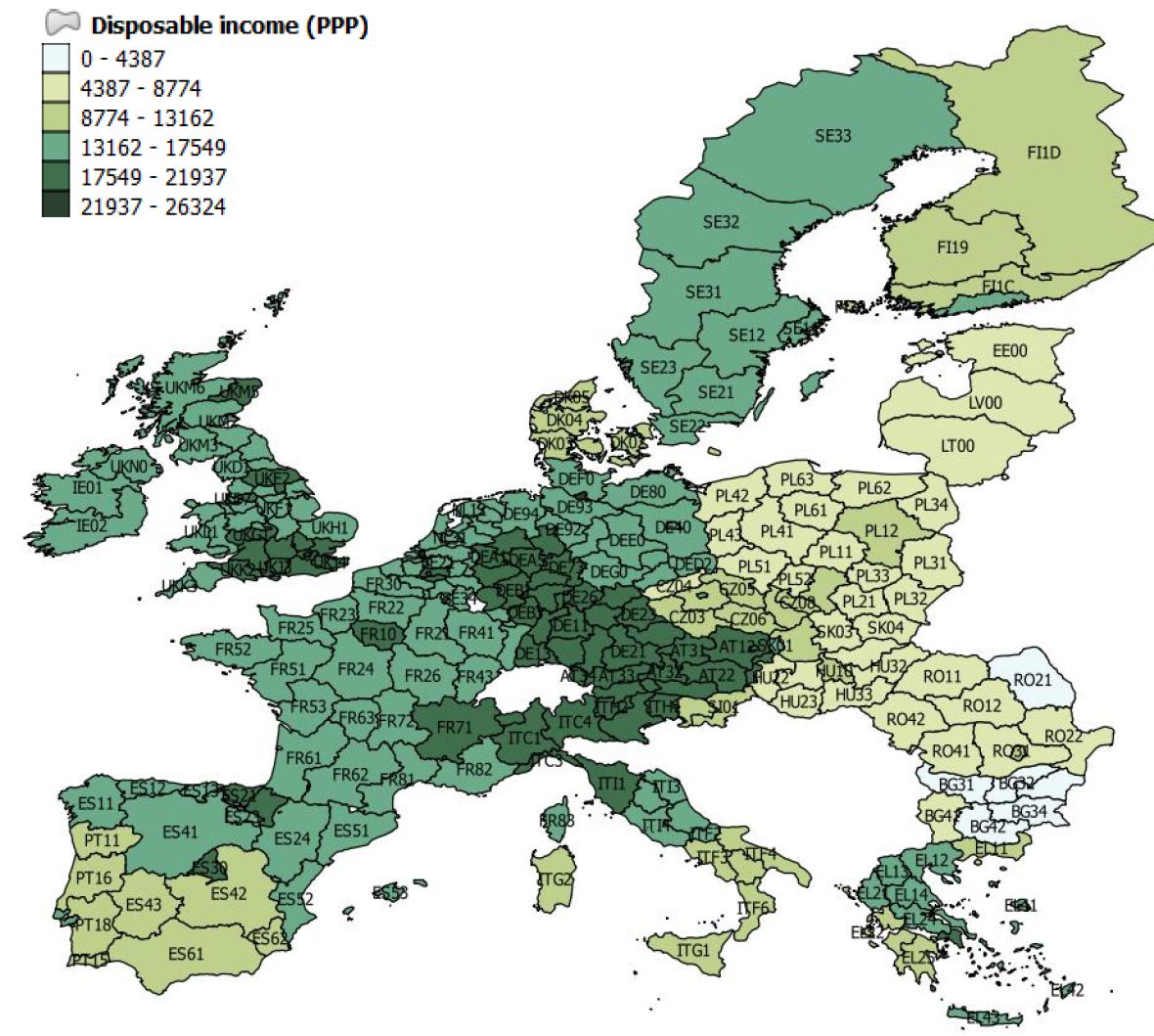
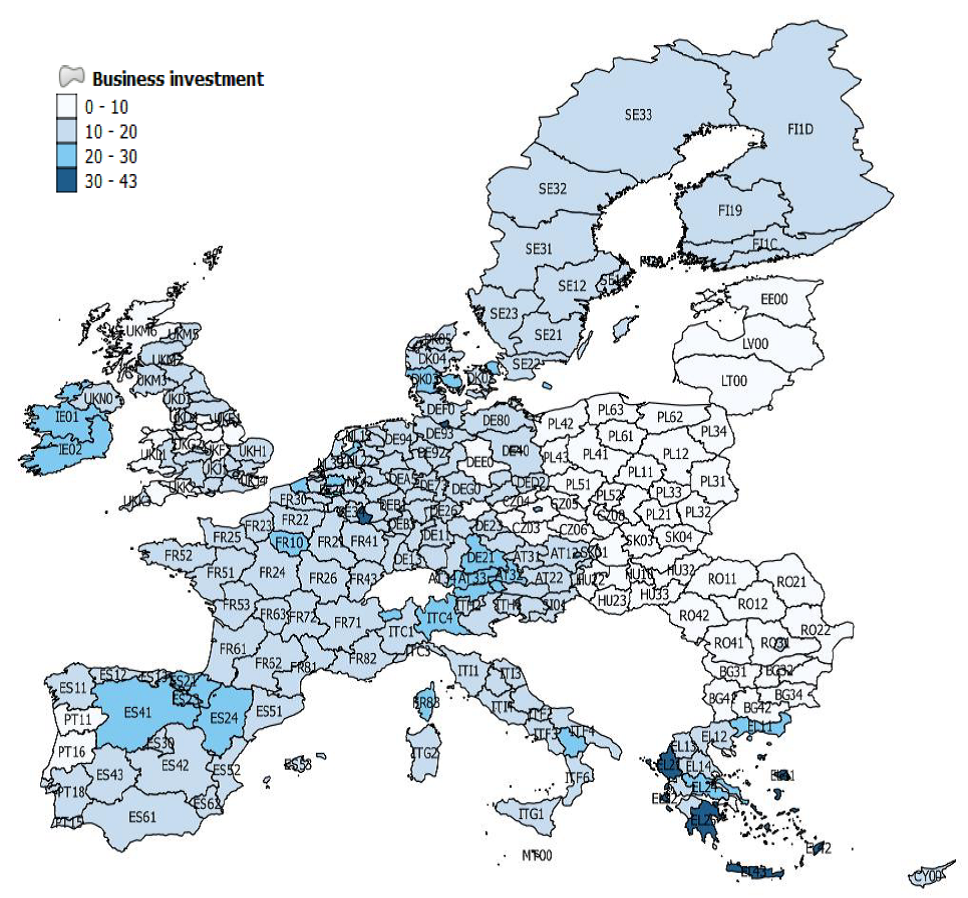
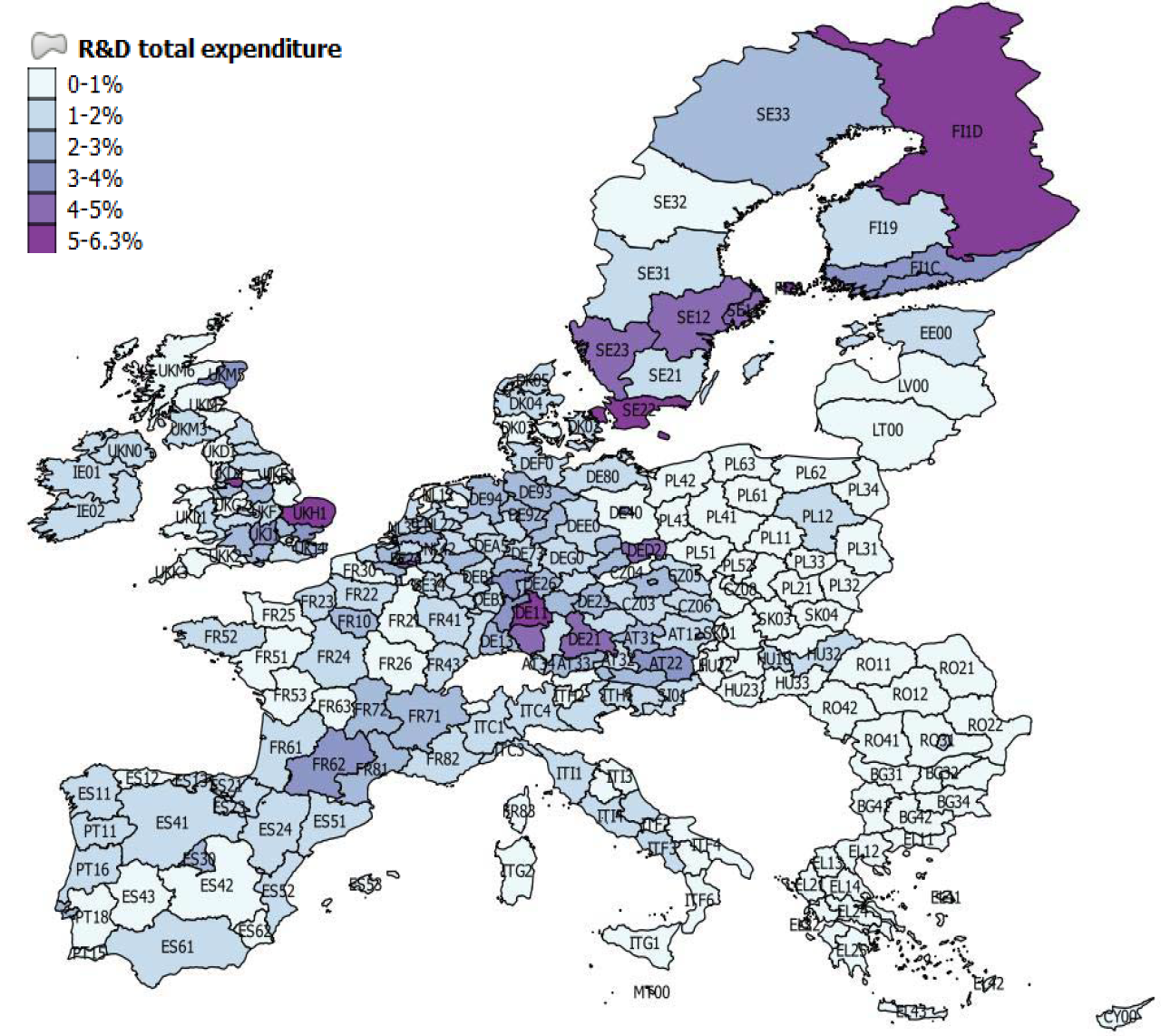
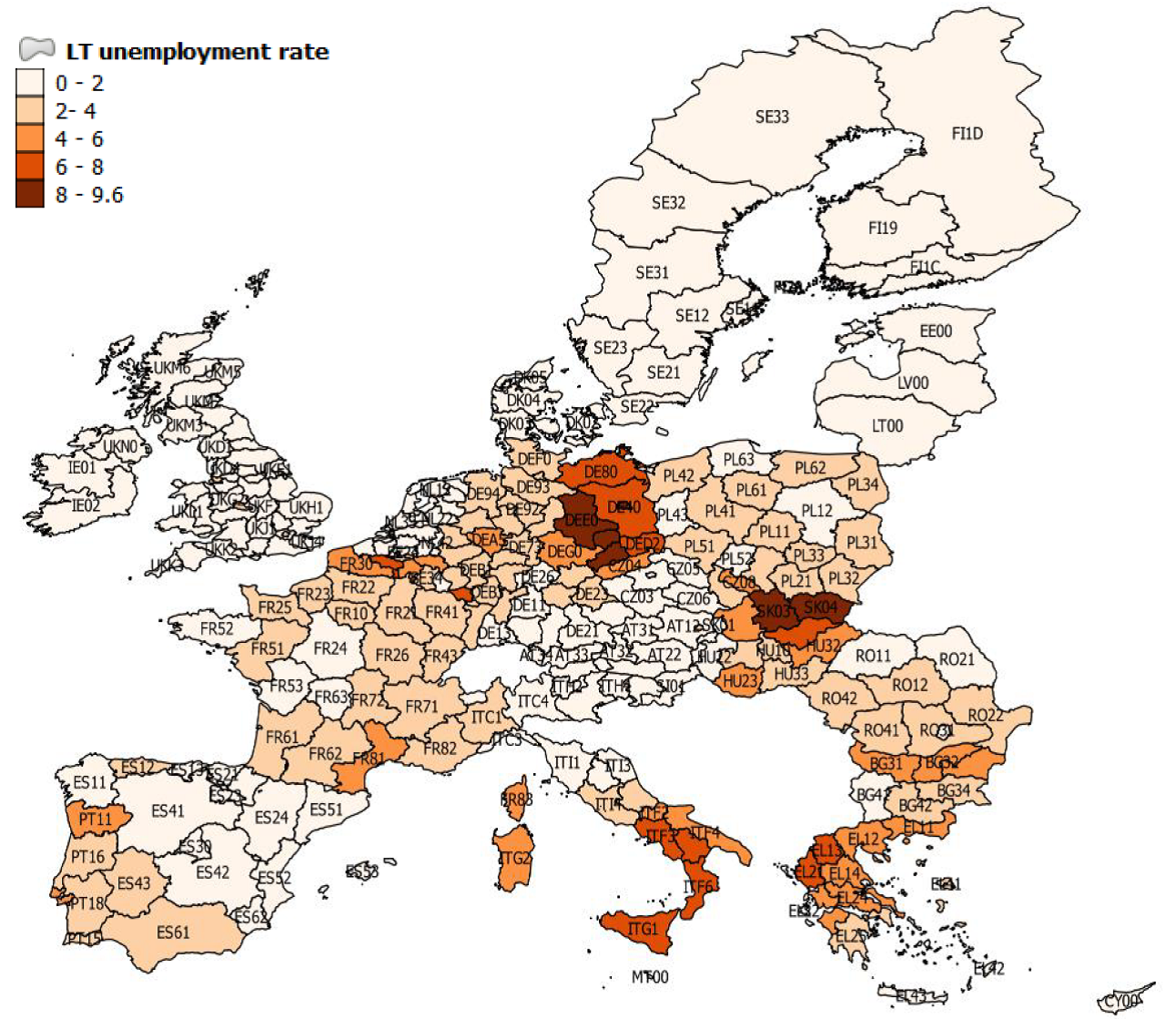
We start our analysis of the dataset with some choropleth maps and scatter plots of simple correlations. Figure 1 shows the geographical distribution of GDP per capita in 2008 (at the end of the sample) across the EU regions. Low-income regions are concentrated in the Central, Eastern and Southeastern Europe (CESEE) countries, as well as in Southern Italy and the south of Spain and Portugal. By contrast, we can identify a concentration of high-income regions in a band going from the London area to Northern Italy, including South-Western Germany, Austria and the South-East of France. The largest European cities are also among the regions with the highest income levels, although more dispersed geographically (e.g. Paris, Madrid, Brussels, Hamburg, Manchester, Edinburgh). Figure 2 provides a similar representation for data on investment per employee. Again, regions in the CESEE countries registered the lowest levels of investment, while the highest levels are in Southern Germany, Austria and Northern Italy. This gives some preliminary evidence of an association between income per capita level and investment expenditures. Some high investment levels are also noticeable in Greece as well as in Spain, which may be related to the sharp increase in construction investment prior to the financial crisis in 2008. Figure 3 shows a similar picture for R&D expenditure. Although the high-income regions in the center of Europe generally show high levels of R&D expenditure ratios, specific regions in the periphery registered the highest ratios, including Finland, the south of Sweden, the regions of Cambridge and Toulouse, all known for either large innovation centers, universities or highly innovative industries. Finally, Figure 4 shows the geographical distribution of long-term unemployment. The highest levels of long-term unemployment are concentrated in a few areas, including Eastern Germany, Slovakia, some regions in Hungary, Greece, southern Italy and northern France. By contrast, the high-income regions generally have very low levels of long-term unemployed people.
Figure 5 provides a correlation analysis between GDP per capita and six different variables commonly associated with income or development level. As seen before, the positive correlation between GDP per capita and investment expenditures is confirmed. Similarly, we find a positive correlation between GDP per capita and innovation (R&D expenditure). Some positive association is also found between GDP per capita and education or percentage of labor considered high-skilled (higher education, tertiary training, skilled migrants). Again, there seems to be a negative correlation between high income and high long-term unemployment rates, which may possibly indicate that high long-term unemployment reflects structural issues that weigh on economic development. This will be further investigated in our empirical analysis.
3 Empirical specification and econometric approach
3.1 Theoretical background
The theoretical background of our research relates to the growth theory literature and the specification chosen can be seen as a Solow (1956) model augmented with human capital and technology level (Mankiw et al. 1992). At the same time, the empirical specification of the model is general enough to also be consistent with the endogenous growth models (Arnold et al. 2007). The augmented Solow model is based on a production function specification whereby output is a function of physical and human capital, labour and technology. As shown by Boulhol et al. (2008), the long-run relationship derived from the augmented Solow model can be estimated either directly in levels or using a specification in growth terms. The estimation of the long-run relationship in levels has been used in the literature (see Mankiw et al. 1992, Hall, Jones 1999, Bernanke, Gürkaynak 2001) to analyse income level differentials and can then be applied to cross country or regional differences in economic performance, measured by GDP per capita in levels. Estimating the model in levels is also consistent with the assessment of steady-state relationships , which is a good benchmark to measure cross-regional structural differences.
The Mankiw et al. (1992) model can be written as:
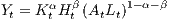 | (1) |
where Y t, Lt, Kt and Ht are output, labour, physical and human capital, respectively and At is the level of technology. Lt and At are assumed to grow at the exogenous rates n and g, respectively. The dynamics of the economy is determined by:
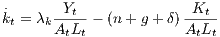 | (2) |
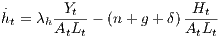 | (3) |
where λk and λh are the investment rates in physical and human capital and δ is the depreciation rate (assumed to be the same for the two types of capital).
Assuming decreasing returns to physical and human capital 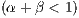 , Eq. (2)
and (3) imply that the economy converges to a steady state (denoted by *) defined
by:
, Eq. (2)
and (3) imply that the economy converges to a steady state (denoted by *) defined
by:
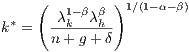 | (4) |
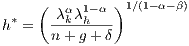 | (5) |
Substituting the two steady-state forms above into (1) and taking logs gives the equation for output per capita, which gives the theoretical basis of our empirical specification:
Equation (6) shows that output per capita depends on initial technology level (A0), technological progress (g), demographic changes (n), investment in physical capital (λk) and the level of human capital (h*). These variables will be included in our empirical specification, where alternative measures of these various factors will be used in the estimation.
3.2 Econometric approach
In regional science, spatial autocorrelation (or spatial dependence) refers to the situation where similar values of a random variable tend to cluster in some locations (Anselin, Bera 1998). The concept of spatial dependence is rather intuitive and has its origins in Tobler’s first law of geography (Tobler 1970): “Everything is related to everything else, but near things are more related than distant things.”
Applied to the economic growth literature, the inclusion of spatial effects implies that economic growth in a given country or region does not only depend on determinants in the country’s own economy (e.g. savings ratio, initial GDP, population growth, technological change etc.), but also on the characteristics of the neighbouring economies (Ertur, Koch 2007).
The spatial econometric literature suggests a range of model specifications to cope with the data generating process behind spatially correlated data. Different spatial model specifications suggest different theoretical and statistical justifications. Alternative spatial regression structures arise when the spatial autoregressive process enters into combination with dependent variables (spatial autoregressive model), explanatory variables (spatial cross-regressive model) or disturbances (spatial error model). In this paper, we use a Spatial Durbin Model (SDM), which makes it possible to include simultaneously two types of spatial dependence: (i) through the dependent and (ii) through the explanatory variables. We find this approach more suitable for our research question, because while investigating the economic development of a given region, the influence of the economic performance and other economic features of neighboring regions could be determinant.
More precisely, we include business investment and human capital development of neighboring regions in our model specification. In this way, we explicitly capture the impact of industrial clusters as well as commuting and inter-regional migration patterns for economic development. In addition, the SDM provides us with larger parameter flexibility. Unlike the traditional spatial autoregressive models, the SDM allows the direct and indirect effects to have opposite signs and a varying ratio for each variable (see Section 4.3)2 .
3.2.1 Model specification
In recent years, the increasing availability of datasets tracking spatial units over time led to a growing interest in the specification and estimation of economic relationships based on spatial panels. Indeed, panel data specifications represent a large number of advantages compared to cross sectional studies. First of all, panel data are more informative and tend to contain more variation and less collinearity among observations (Elhorst 2014). Second, panel data specifications tend to increase efficiency in the estimation because of a greater degree of freedom. Panel specifications also allow addressing more complicated behavioural hypothesis, including effects that cannot be addressed using solely cross-sectional data (Baltagi 2013, Hsiao 2007).
Spatial variables are likely to differ in their background variables that may affect the dependent variable in a given spatial unit. Nevertheless, these space-specific variables tend to be difficult to measure or hard to obtain. For instance, being located close to the border or seaside, in an urban or rural area, or at the center/periphery may be a determinant to explain a socio-economic phenomenon. Overlooking these space-specific peculiarities may again lead to biased parameter estimates. A solution to this is to introduce an intercept ξi into the specification that captures the effect of the space-specific omitted variables. In the same way, the inclusion of the time-period specific effects controls for spatial-invariant time effects such as a specific year marked by an overall economic recession, the business cycle, introduction of new industrial policies in a given year, change in legislation, etc.
The space-time econometric model for a panel of N observations over T periods of time can be written as a SDM3 , specified as follows:
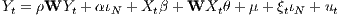 | (7) |
where Y t is a N × 1 vector of dependent variables, ιN is an N × 1 vector of ones associated
with the constant term parameter α and ρ is the spatial autoregressive parameter. W is a
non-negative N × N spatial weights matrix describing the arrangement of the units in space
relative to their neighbours (with zero diagonal elements by assumption) and WY t is a spatial
vector representing a linear combination of the values of the dependent variable vector
from the neighbouring regions. Xt is the matrix of own characteristics and WXt is
the spatial lag matrix of the linear combination of the values of the explanatory
variables from neighbouring observations. ρ and θ capture the strength of spatial
interactions working through the dependent and explanatory variables, respectively. ut
is the stochastic error term which – for the sake of simplicity – is assumed to be
i.i.d. N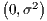 . While μ is the time specific fixed effect, ξtιN is the spatial fixed
effect.
. While μ is the time specific fixed effect, ξtιN is the spatial fixed
effect.
In spatial panel models, spatial and time-period fixed effects may be treated as fixed or random effects in the same way as in traditional panel specifications4 . The random effects model specification appears more suitable to our sample (with a relatively large N dimension), due to a smaller loss of degrees of freedom compared to the fixed effect model5 . More importantly, the random effect specification makes it possible to estimate the coefficients of the time-invariant variables and variables that only vary a little.
In other words, the fixed-effect model would not be perfectly suitable for the analysis of economic development, which traditionally includes the level of initial GDP as an explanatory variable, as well as country dummies and possibly other structural variables that vary only marginally in time. However, as a robustness check, we also estimate the specifications reported in Tables 1 and 2 (without the initial GDP level variable and country dummies) with fixed effects. The results (available upon request) do not show qualitative differences regarding the significance level and associated signs of the parameter estimates. However, the associated coefficients, including the spatially lagged variables, are of greater magnitude in fixed effects estimations. This is probably related to omitted variables (initial GDP and country dummies) whose impact is captured by other variables. Not surprisingly, the fixed effect estimations have smaller R-squared values, suggesting a better fit of the random effect model.
In the SDM, the inclusion of the spatially lagged dependent variable into the right-hand side creates endogeneity, as the spatially lagged dependent variable WY is correlated with the error term u. As a consequence, the estimation of the SDM with the OLS estimator may generate biased and inconsistent parameters and statistical inferences. Thus, in this study we use the maximum likelihood estimator proposed by Anselin (1988).
Parameters generated by spatial models which include simultaneously spatial interactions with the dependent variable, exogenous variables and the error term may be hard to interpret in a meaningful way because of the difficulty of distinguishing these interactions from each other. Therefore, in the SDM specification above we chose to only consider spatial endogenous and exogenous interactions and disregard possible spatial autocorrelation in the error term. LeSage, Pace (2009, pp. 155-158) point out that ignoring spatial autocorrelation in the error term would only cause loss of efficiency (through the inferences). On the other hand, ignoring spatial autocorrelation in the dependent or exogenous variables would require omitting relevant explanatory variables from the regression equation and may generate biased and inconsistent estimates of model parameters.
3.2.2 Partial derivatives
In traditional linear regression analyses, it is assumed that observations are independent from other. Therefore, the parameter estimates can be straightforwardly interpreted as the partial derivative of the dependent variable with respect to the explanatory variable. However, in models with spatially lagged variables, the parameter estimates also include information from the neighbours, which complicates the interpretation of the estimated parameters.
Thus, models that contain spatially lagged dependent variables exhibit a complicated derivative structure, where the standard regression coefficient interpretation of coefficient estimates as partial derivatives no longer holds:
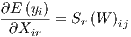 |
Following LeSage, Pace (2009), the total impact arising from a change in explanatory
variable Xr is reflected by all elements of the matrix Sr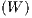 . The matrix expression of the own
and cross partial derivatives can be expressed as follows:
. The matrix expression of the own
and cross partial derivatives can be expressed as follows:
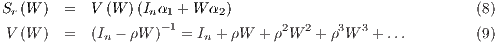
This can be broken down into direct, indirect (spatial spillovers impacts) and total impacts
arising from a change in the variable Xr on average across all observations. While the diagonal
elements of the N ×N matrix Sr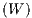 correspond to direct impacts, the off-diagonal elements
represent indirect impacts. The direct effects can be used to test the hypothesis whether an
explanatory variable has a significant effect on the dependent variable in its own economy and
the indirect effects test the hypothesis whether spatial spillovers from this variable
exist.
correspond to direct impacts, the off-diagonal elements
represent indirect impacts. The direct effects can be used to test the hypothesis whether an
explanatory variable has a significant effect on the dependent variable in its own economy and
the indirect effects test the hypothesis whether spatial spillovers from this variable
exist.
The partial derivative structure of spatial models present a reporting challenge as a dataset with N spatial units and K explanatory variables would generate K times N × N matrices of direct and indirect effects. LeSage, Pace (2009) propose to report one summary indicator for direct effects which is the average of the main diagonal elements (i.e. own partial derivatives), and one summary indicator for indirect effects, which is the average of the column (or row) sums of the off-diagonal elements of the matrix6 .
4 Empirical evidence
4.1 Distance matrix
The modelling of spatial effects requires an appropriate representation of spatial arrangement of observations. Distance-based matrices are widely used in the literature because of their exogenous nature to economic phenomenon (otherwise endogenous distance matrices would induce high non-linearity into the model). There are several types of distance-based spatial weights matrices based on contiguity (border sharing), inverse distance or a fixed number of the nearest neighbours.
In the case of our dataset, a distance matrix based on border sharing criteria contiguity would not be adequate as all countries in regional Europe do not necessarily belong to the EU. As a result, we have some empty polygons in our map (e.g. Norway, Switzerland). Therefore, we define the spatial structure as a distance decay function considering that the strength of spatial interactions declines with distance. In addition, we assume that beyond a certain critical bilateral geographic distance, interactions between provinces become negligible. To test the robustness of our results, we specify two alternative inverse distance matrices with 50km and 100km, as respective cut-off distances7 .
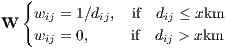 |
W consists of individual spatial weights wij that typically reflect the “spatial influence” of unit j on unit i. dij is the great-circle distance (calculated from the Haversine formula) between observation i and j8 W is row-standardised by dividing each weight of an observation by the corresponding row sum wij∕∑ jwij. Whereas the original inverse-distance spatial weighting matrix is symmetric, the row-standardised one is not. This implies that, region i could have a larger influence on the random variable of interest in region j and vice-versa. By convention, the distance matrix has zeros on the main diagonal, thus no observation predicts itself.
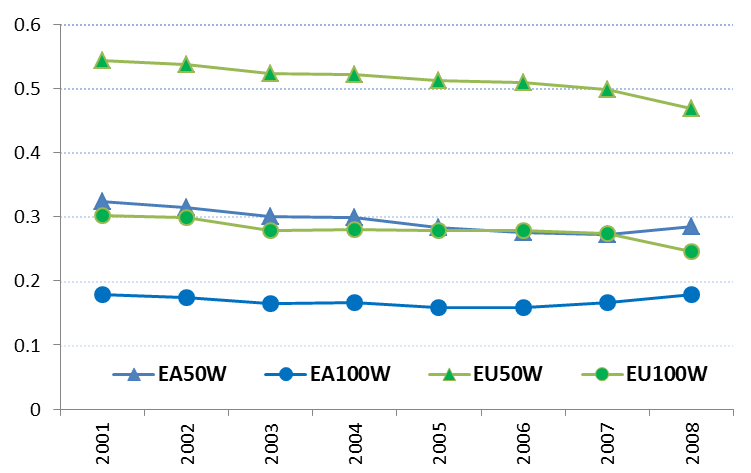
Notes: All reported Moran’s I coefficients are statistically significant at the 1% level (based on z-scores), GDP
per capita in natural logarithm.
4.2 Spatial autocorrelation measure
Moran’s I statistic (Moran 1950) is the most widely used measure to detect spatial autocorrelation. In other words, it evaluates whether the distribution pattern of a variable is clustered, dispersed, or random.
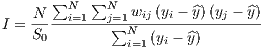 |
where wij is the element of the matrix W corresponding to the observation pair i and j. S0 is
the sum of all wij’s and 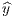 is the mean value of the variable of interest and N is the number of
locations.
is the mean value of the variable of interest and N is the number of
locations.
Moran’s I statistic could be interpreted as the statistic measure of the covariance of the observations in nearby provinces relative to the variance of the observations across regions. The Moran’s I test is based on the null hypothesis of absence of the clustering in some geographical areas. In a given year t, an index value close to 1 indicates clustering while an index value close to -1 indicates dispersion.
Moran’s I statistics for GDP per capita reported below are based on two alternative distance matrix specifications with different cut-off points9 . The positive Moran’s I statistics in Figure 6 show that over the entire period of study, GDP per capita in the EU and euro area was spatially autocorrelated. In other words, GDP per capita was not randomly distributed across the EU regions and high- (low-) income values tended to cluster geographically. In addition, higher Moran’s I statistics for the EU reveal stronger clustering in GDP per capita compared to the euro area. As expected, the magnitude of spatial interactions decays with distance. For both the EU and the euro area, the Moran’s I coefficients are smaller for the matrix using 100km as cut-off distance. The results also show that in the EU, the level difference in Moran’s I statistics generated by the two matrices are larger, probably reflecting the spread of countries across a larger geographic area.
4.3 Variables used as determinants of GDP per capita
The theoretical background presented above has determined the empirical specification used in this paper. Equation (6) includes the initial technology level, technological progress, demographic changes or labour market conditions, investment in physical capital and the level of human capital as the determinants of GDP per capita. Table 1 presents the variables used in the empirical exercise, the expected signs, and interpretation of the associated coefficients. After having tested alternative specifications including other variables available in the database we only report the most parsimonious ones with good statistical properties.
| Variable | Sign | Interpretation | |
| Dependent variable | |||
| GDP per capita | Measure of economic performance | ||
| Initial technogical level | |||
| Initial GDP per capita | + | Knowledge available and distance to technolo- | |
| gical frontier | |||
| Innovation | |||
| R&D public expenditure | + | Indicator of science and technology policies | |
| Demographic/labour | |||
| Pop. aged 15-34 | + | Young population | |
| Skilled migrants | + | Demographic changes from migration of | |
| skilled workers | |||
| Long-term unemployment | – | Degree of labour market rigidity and skill mis- | |
| match | |||
| Physical capital | |||
| Business investment | + | Accumulation of physical capital | |
| Human capital | |||
| Tertiary education | + | Socio-economic conditions in educational | |
| achievements | |||
Given that the empirical modelling approach includes spillover effects from neighbouring regions through the spatially lagged dependent and explanatory variables, the drivers of economic performance will also include such external factors. We expect generally positive spillovers, confirming the economic benefits coming from knowledge and/or investment intensive neighbours. However, we cannot exclude possible crowding out effects in terms of investment (e.g. the attraction of investors in a region may reduce their investment in neighbouring regions) or human capital.
The SDM specification allows negative spillovers (indirect effects) from the neighbours although the direct effects (i.e. the impact of the explanatory variable on its own region) are positive. These potentially complex relationships could not be modelled with the use of, e.g., a spatial autoregressive model (SAR)10 , because in a SAR model the direct (the impact of a change in investment on its own economic performance) and the indirect effects (the impact of the same change on the economic performance of the neighbours and coming back to the region) have, by construction, the same sign. Furthermore, the ratio, indirect to direct effect, is identical in a SAR model for every explanatory variable (LeSage, Pace 2009, Elhorst 2012, Pace, Zhu 2012).
4.4 Empirical results
We conduct our empirical analysis based on the specification determined by Eq. (6) and using the variables included in Table 1. We run regressions both for the entire EU sample and for a sample restricted to euro area regions, using in all cases random-effect specifications as explained above. To account for country-specific effects, we include country dummies in our regressions. These dummies capture country-specific effects, such as economic policies taken at the national level (taxation, industrial policies and regulations in product and labour markets, …). Concerning the distance matrix, we present here results based on the matrix with 50km as cut-off distance11 .
| Dep. var.: ln(GDP per capita) | [1] | [2] | [3] | [4]
| ||||
ρ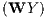 | 0.85 | *** | 0.86 | *** | 0.71 | *** | 0.70 | *** |
Φ1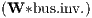 | 0.003 | *** | 0.006 | *** | 0.006 | *** | 0.002 | *** |
Φ2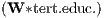 | - | - | 0.002 | *** | 0.002 | *** | ||
| Number of obs. | 2024 | 2024 | 2024 | 2024
| ||||
| R2 | 0.82 | 0.81 | 0.88 | 0.89
| ||||
| Log-likelihood | 1991 | 1999 | 2217 | 2213
| ||||
| DIRECT | ||||||||
| GDP per capita (initial) | 0.94 | *** | 0.92 | *** | 0.71 | *** | 0.70 | *** |
| Business investment | 0.007 | *** | 0.008 | *** | 0.005 | *** | 0.005 | *** |
| R&D expenditure (% of GDP) | 0.12 | *** | 0.13 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.01 | *** | 0.01 | *** | -
| ||
| Skilled migrants | - | - | - | 0.01 | *** | |||
| Long-term unemployment | - | - | -0.02 | *** | -0.02 | *** | ||
| Tertiary education | - | - | 0.003 | *** | 0.004 | *** | ||
| INDIRECT | ||||||||
| GDP per capita (initial) | 4.53 | *** | 4.80 | *** | 1.62 | *** | 1.47 | *** |
| Business investment | 0.05 | *** | 0.07 | *** | 0.03 | *** | 0.02 | *** |
| R&D expenditure (% of GDP) | 0.60 | *** | 0.67 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.07 | *** | 0.03 | *** | -
| ||
| Skilled migrants | - | - | - | 0.03 | *** | |||
| Long-term unemployment | - | - | -0.04 | *** | -0.04 | *** | ||
| Tertiary education | - | - | 0.02 | *** | 0.02 | *** | ||
| TOTAL | ||||||||
| GDP per capita (initial) | 5.48 | *** | 5.72 | *** | 2.34 | *** | 2.17 | *** |
| Business investment | 0.06 | *** | 0.08 | *** | 0.03 | *** | 0.02 | *** |
| R&D expenditure (% of GDP) | 0.73 | *** | 0.79 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.08 | *** | 0.05 | *** | -
| ||
| Skilled migrants | - | - | - | 0.04 | *** | |||
| Long-term unemployment | - | - | -0.06 | *** | -0.06 | *** | ||
| Tertiary education | - | - | 0.02 | *** | 0.02 | *** | ||
| Dep. var.: ln(GDP per capita) | [1] | [2] | [3] | [4]
| ||||
ρ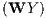 | 0.70 | *** | 0.71 | *** | 0.66 | *** | 0.63 | *** |
Φ1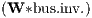 | 0.010 | *** | 0.011 | *** | 0.008 | *** | 0.007 | *** |
Φ2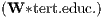 | - | - | 0.003 | *** | 0.003 | *** | ||
| Number of obs. | 1264 | 1264 | 1264 | 1264
| ||||
| R2 | 0.86 | 0.85 | 0.87 | 0.89
| ||||
| Log-likelihood | 1599 | 1600 | 1670 | 1681
| ||||
| DIRECT | ||||||||
| GDP per capita (initial) | 0.97 | *** | 0.97 | *** | 0.83 | *** | 0.76 | *** |
| Business investment | 0.006 | *** | 0.007 | *** | 0.006 | *** | 0.005 | *** |
| R&D expenditure (% of GDP) | 0.09 | *** | 0.09 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.003 | *** | 0.008 | *** | -
| ||
| Skilled migrants | - | - | - | 0.02 | *** | |||
| Long-term unemployment | - | - | -0.01 | *** | -0.01 | *** | ||
| Tertiary education | - | - | 0.003 | *** | 0.003 | *** | ||
| INDIRECT | ||||||||
| GDP per capita (initial) | 2.05 | *** | 2.13 | *** | 1.44 | *** | 1.16 | *** |
| Business investment | 0.04 | *** | 0.05 | *** | 0.03 | *** | 0.02 | *** |
| R&D expenditure (% of GDP) | 0.20 | *** | 0.21 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.007 | *** | 0.01 | *** | -
| ||
| Skilled migrants | - | - | - | 0.03 | *** | |||
| Long-term unemployment | - | - | -0.02 | *** | -0.02 | *** | ||
| Tertiary education | - | - | 0.01 | *** | 0.01 | *** | ||
| TOTAL | ||||||||
| GDP per capita (initial) | 3.02 | *** | 3.10 | *** | 2.27 | *** | 1.92 | *** |
| Business investment | 0.05 | *** | 0.05 | *** | 0.04 | *** | 0.03 | *** |
| R&D expenditure (% of GDP) | 0.29 | *** | 0.30 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.01 | *** | 0.02 | *** | -
| ||
| Skilled migrants | - | - | - | 0.05 | *** | |||
| Long-term unemployment | - | - | -0.03 | *** | -0.03 | *** | ||
| Tertiary education | - | - | 0.02 | *** | 0.01 | *** | ||
Tables 2 and 3 present the results for the whole EU sample and a euro area subsample
respectively. After having tested a number of alternative specifications, we only report those
yielding significant coefficients. The four specifications reported include the initial level of GDP
per capita and business investment, but differ according to the measures of innovation, human
capital or demographic/labour market indicators. Starting with the spatially lagged variables,
the first interesting result concerns the large and significant spatial autoregressive coefficient
ρ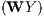 confirming that being surrounded by low(high) income regions is a significant
determinant of economic performance for a given region. In addition, the large spatial
autoregressive coefficients in all specifications confirm the presence of significant
spatial feedback effects where strong indirect effects reinforce direct effects. We also
find that the investment going to the neighbouring regions, Φ1
confirming that being surrounded by low(high) income regions is a significant
determinant of economic performance for a given region. In addition, the large spatial
autoregressive coefficients in all specifications confirm the presence of significant
spatial feedback effects where strong indirect effects reinforce direct effects. We also
find that the investment going to the neighbouring regions, Φ1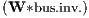 , has
a positive effect on economic development of a given region, ruling out a possible
crowding out effect on investment. This confirms our intuition that industrial clusters
(i.e. highly invested regions) are important drivers of economic development. In
the same way, the availability of well-educated human capital, Φ2
, has
a positive effect on economic development of a given region, ruling out a possible
crowding out effect on investment. This confirms our intuition that industrial clusters
(i.e. highly invested regions) are important drivers of economic development. In
the same way, the availability of well-educated human capital, Φ2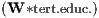 ,
in the neighbouring regions is found to have a positive impact on own economic
development, most probably through commuting and inter-regional migration of the skilled
workforce.
,
in the neighbouring regions is found to have a positive impact on own economic
development, most probably through commuting and inter-regional migration of the skilled
workforce.
Moving to the other explanatory variables, traditional variables used in the literature are found significant. We find in all specifications a positive impact of initial GDP per capita, which proxies the initial technology level (i.e. the closer to the technological frontier, the higher the performance). The accumulation of both physical capital (business investment) and human capital (tertiary education) appear to significantly determine regional income. Demographic factors have also a positive and significant impact on income level, such as the share of young population (population aged 15-34) or demographic changes from migration of skilled workers. Concerning innovation, only public R&D expenditure is found to be statistically significant, which may point to the role of European governments in financing innovation, either to complement market failures or to provide financing at seed and initial stage. Finally, the negative coefficient of long-term unemployment is likely to signal that labour market rigidities and/or skill mismatch create inefficiencies hindering economic performance.
The results show the presence of significant indirect effects. We interpret the indirect effect of initial GDP per capita (which is a time invariant variable) as follows: a high level of technology also helps the development of surrounding regions, leading to positive spillovers reinforcing the initial direct effects. The economic interpretation of the other indirect effects is rather straightforward; overall they amplify the direct impact of the explanatory variable through spatial feedbacks (i.e. the spatial multiplier effect).
The majority of country dummies are found to be significant, showing the relevance of country-specific effects in explaining economic performance. Therefore, the inclusion of these dummies improves the performance of the model estimations, while not qualitatively changing the outcomes of the estimations (see Appendix Tables A.3 and A.4 for estimates excluding country dummies for the EU and the euro area samples respectively).
Finally, the results for the euro area subsample are fairly similar to those of the whole
EU, showing that our specification is robust to different country samples. A few
differences are however worth pointing out. First, the spatial autoregressive coefficient
ρ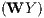 is higher for the EU sample, which leads to significantly larger feedback
effects complementing the direct effects. Moreover, the coefficient of initial GDP per
capita is higher for the euro area as regards the indirect effects, meaning that the
initial level of technology is more important to explain economic performance in the
euro area than in the EU regions. Given the larger presence of mature economies
in the euro area sample this result appears rather intuitive: an economy initially
close to the technological frontier is expected to remain among the best performers
over time. Indeed, technology diffusion is a slow process requiring long periods to
significantly enhance economic performance. However, due to data limitations, the
initial GDP in 2000 is too close to the end period of 2008 to allow for the diffusion
process to fully take place. Concerning total effects, the EU sample has nevertheless
stronger coefficients associated with initial GDP per capita, driven by stronger indirect
effects.
is higher for the EU sample, which leads to significantly larger feedback
effects complementing the direct effects. Moreover, the coefficient of initial GDP per
capita is higher for the euro area as regards the indirect effects, meaning that the
initial level of technology is more important to explain economic performance in the
euro area than in the EU regions. Given the larger presence of mature economies
in the euro area sample this result appears rather intuitive: an economy initially
close to the technological frontier is expected to remain among the best performers
over time. Indeed, technology diffusion is a slow process requiring long periods to
significantly enhance economic performance. However, due to data limitations, the
initial GDP in 2000 is too close to the end period of 2008 to allow for the diffusion
process to fully take place. Concerning total effects, the EU sample has nevertheless
stronger coefficients associated with initial GDP per capita, driven by stronger indirect
effects.
4.5 Comparison with previous studies
The variables used as determinants of regional growth are similar to Rodriguez-Pose, Crescenzi (2008), and, like them, we find significant contributions to innovation and innovative spillovers across regions. However, while they ignored a few key determinants of economic performance, like business investment or skilled migrants, our results show their important contribution to regional economic performance. Moreover, unlike Rodriguez-Pose, Crescenzi (2008), who do not find any significant role for long-term unemployment, this determinant appears as a key negative factor for economic performance in our empirical evidence. Finally, our results show stronger regional spillovers, which could be explained by important differences in the modelling approach. While Rodriguez-Pose, Crescenzi (2008) obtain their empirical evidence by estimating heteroskedasticity-consistent OLS regressions, we chose to use SDM specifications to model explicitly cross-regional spillovers. Like Wagner, Zeileis (2017), initial GDP and the share of highly educated in the working age population also significantly explains economic development. However, while they find that the investment share in physical capital is only significant for coastal regions in the EU peripheral countries, our results clearly point to a key role given to business investment in explaining heterogeneity in economic performance. This difference may be explained by the fact that Wagner, Zeileis (2017) use data that mix private and public capital. Such a limitation seems to lead to a critical underestimation of the role of business investment (in a given region but also in its neighbours) in the growth process. Their study also ignores the role of innovation and skilled migrants as determinants of economic performance and does not take into account long-term unemployment as a structural barrier to growth. These variables also appear as key determinants in our results.
Overall, thanks to the use of the original data included in the European Cluster Observatory dataset, our results appear closer to the theoretical prediction given by the human-capital-augmented Solow-type growth equation à la Mankiw et al. (1992). Moreover, our modelling approach based on the SDM enables us to explicitly capture spatial effects from neighbouring regions. Finally, studying within the EU sample the subset of regions belonging to the euro area, brings additional insights concerning the role of the initial level of technology to explain economic performance in more advanced economies.
5 Concluding remarks
Our results show that social-economic environment and traditional determinants of economic performance (distance from innovation frontier, physical and human capital and innovation) are significant. They also confirm the relevance of spatial spillovers, whereby strong indirect effects reinforce direct effects. In particular, we find that business investment and human capital of the neighbouring regions have a positive impact – both direct and indirect – on economic performance of a given region. At the same time, structural inefficiencies related to labour market rigidities and/or skill mismatch are found to hinder economic performance. These results encourage the pursuit of structural reforms in stressed European countries and, if possible, at the regional level to boost growth and competitiveness.
Overall, our results confirm the existence of high-income clusters (mostly located in the center of Western Europe) and their positive effects on the development of the neighbouring regions. From a policy perspective, this implies that the creation of growth poles specialised in innovative and high growth potential activities could be a strategy for Europe to catch up with the US in terms of technology and trend output. Our methodological approach focuses on the summary measures of the average spatial effects. Further research is warranted in identifying and quantifying the spillovers coming from specific clusters in a regional or European context. Furthermore, with better data availability exploring the sectoral dimension of the clusters would be insightful.
References
Abreu M, DeGroot H, Florax L, J R (2005) Space and growth: A survey of empirical evidence and methods. Région et Développement 21: 13–44
Aghion P, Howitt. P (1992) A model of growth through creative destruction. Econometrica 60[2]: 323–351. CrossRef.
Anselin L (1988) Spatial Econometrics: Methods and Models. Kluwer Academic, Dordrecht. CrossRef.
Anselin L, Bera A (1998) Spatial dependence in linear regression models with an introduction to spatial econometrics. In: Ullah A, E. D, Giles A (eds), Handbook of Applied Economic Statistics. Marcel Dekker, New York, 237–289
Anselin L, Le Gallo J, Jayet H (2008) Spatial panel econometrics. In: Matyas L, Sevestre P (eds), The Econometrics of Panel Data, Fundamentals and Recent Developments in Theory and Practice (3rd ed.). Springer-Verlag, Berlin, 627–662. CrossRef.
Arnold J, Bassanini A, Scarpetta S (2007) Solow or Lucas?: Testing growth models using panel data from OECD countries. OECD Working Paper No 592
Baltagi B (2013) Econometric analysis of panel data (5th ed.). Wiley, Chichester
Bernanke BS, Gürkaynak RS (2001) Is growth exogenous? Taking Mankiw, Romer and Weil seriously. NBER Macroeconomics Annual
Boulhol H, de Serres A, Molnar M (2008) The contribution of geography to GDP per capita. OECD Journal: Economic Studies. CrossRef.
Bush V (1945) Science: The endless frontier. U.S. Office of Scientific Research and Development, Report to the President on a Program for Postwar Scientific Research, Government Printing Office, Washington, D.C.
Crescenzi R (2005) Innovation and regional growth in the enlarged Europe: The role of local innovative capabilities, peripherality, and education. Growth and Change 36: 471–507. CrossRef.
Crescenzi R, Rodriguez-Pose A (2012) Infrastructure and regional growth in the European Union. Papers in Regional Science 91[3]: 487–615. CrossRef.
Crescenzi R, Rodríguez-Pose A, Storper. M (2007) The territorial dynamics of innovation: A Europe-United States comparative analysis. Journal of Economic Geography 7[6]: 673–709. CrossRef.
Elhorst JP (2012) Dynamic spatial panels: Models, methods and inferences. Journal of Geographical Systems 14: 5–28. CrossRef.
Elhorst JP (2013) Spatial panel models. In: Fischer MM, Nijkamp P (eds), Handbook of Regional Science. Springer, Berlin, Chapter 82. CrossRef.
Elhorst JP (2014) Spatial econometrics: From cross-sectional data to spatial panels. Springer, Berlin New York Dordrecht London. CrossRef.
Ertur C, Koch W (2007) Growth, technological interdependence and spatial externalities: Theory and evidence. Journal of Applied Econometrics 22: 1033–1062. CrossRef.
European Commission (2010a) Europe 2020: A strategy for smart sustainable and inclusive growth. COM (2010) 2020
European Commission (2010b) Regional policy contributing to smart growth in Europe 2020. Communication from the Comission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the regions. COM(2010) 553
Evangelista R, Meliciani V, Vezzani A (2018) Specialisation in key enabling technologies and regional growth in Europe. Economics of Innovation and New Technology 27[3]
Grossman GM, Helpman E (1991) Innovation and Growth in the Global Economy. MIT Press, Cambridge, MA
Hall R, Jones C (1999) Why do some countries produce so much more output per worker than others? Quarterly Journal of Economics 114[1]: 83–116. CrossRef.
Hasan I, Koetter M, Wedow M (2009) Regional growth and finance in Europe: Is there a quality effect of bank efficiency? Journal of Banking and Finance 33[8]: 1446–1453. CrossRef.
Hsiao C (2007) Panel data analysis – Advantages and challenges. TEST: An Official Journal of the Spanish Society of Statistics and Operations Research 16[1]: 1–22
Jaffe A, Trajtenberg M, Henderson R (1993) Geographic localization of knowledge spillovers as evidenced by patent citations. Quarterly Journal of Economics 108[3]: 577–98. CrossRef.
Ketels C, Protsiv S (2014) Methodology and finding report for a cluster mapping of related sectors. European Cluster Observatory Report. European Commission
LeSage J, Pace R (2009) Introduction to Spatial Econometrics. CRC Press, Boca Raton, FL. CrossRef.
LeSage JP (2014) What regional scientists need to know about spatial econometrics. The Review of Regional Studies 44[1]: 13–32
Maclaurin W (1953) The sequence from invention to innovation and its relation to economic growth. Quarterly Journal of Economics 67[1]: 97–111. CrossRef.
Mankiw GN, Romer D, Weil D (1992) A contribution to the empirics of economic growth. Quarterly Journal of Economics 107[2]: 407–437. CrossRef.
Moran PAP (1950) A test for the serial dependence of residuals. Biometrika 37: 178–181. CrossRef.
Pace RK, Zhu S (2012) Separable spatial modeling of spillovers and disturbances. Journal of Geographical Systems 14[1]: 75–90. CrossRef.
Porter M (1990) The Competitive Advantage of Nations. The Free Press, New York. CrossRef.
Rodriguez-Pose A (2014) Innovation and regional growth in Mexico: 2000-2010. CEPR Discussion Paper No. 10153
Rodriguez-Pose A, Crescenzi R (2008) R&d, spillovers, innovation systems and the genesis of regional growth in Europe. Regional Studies 42[1]: 51–67
Solow R (1956) A contribution to the theory of economic growth. Quarterly Journal of Economics 70[1]: 65–94
Tobler W (1970) A computer movie simulating urban growth in the Detroit region. Economic Geography 46: 234–40. CrossRef.
Usai S (2011) The geography of inventive activities in OECD regions. Regional Studies 45[6]: 711–731. CrossRef.
Wagner M, Zeileis A (2017) Heterogeneity and spatial dependence of regional growth in the EU: A recursive partitioning approach. German economic review, forthcoming
 © 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
© 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
A Appendix A
| Dep. var.: ln(GDP per capita) | [1] | [2] | [3] | [4]
| ||||
| Germany (benchmark) | - | - | - | -
| ||||
| Austria | 1.73 | *** | 1.85 | *** | 0.51 | * | 0.51 | ** |
| Belgium | -0.22 | -0.39 | -0.23 | -0.20 | ||||
| Bulgaria | 7.59 | *** | 7.42 | *** | 1.76 | *** | 1.68 | *** |
| Cyprus | 3.89 | *** | 3.44 | *** | 1.20 | * | 1.37 | ** |
| Czech Rep. | 4.63 | *** | 4.34 | *** | 0.98 | *** | 1.10 | *** |
| Denmark | -0.56 | -0.57 | -0.66 | ** | -0.57 | ** | ||
| Estonia | 4.75 | *** | 4.61 | *** | 0.58 | 0.57 | ||
| Spain | 2.03 | *** | 1.64 | *** | 0.16 | 0.37 | * | |
| Finland | 2.91 | *** | 3.21 | *** | 0.31 | 0.33 | ||
| France | 2.51 | *** | 2.55 | *** | 0.95 | *** | 0.95 | *** |
| Greece | 3.85 | *** | 3.89 | *** | 1.24 | *** | 1.36 | *** |
| Hungary | 6.41 | *** | 6.20 | *** | 1.41 | *** | 1.42 | *** |
| Ireland | 0.44 | 0.02 | -0.17 | 0.13 | ||||
| Italy | 0.90 | *** | 0.86 | *** | -0.12 | -0.01 | ||
| Lithuania | 5.09 | *** | 4.92 | *** | 0.65 | 0.75 | ||
| Luxembourg | 0.73 | 0.69 | 0.95 | 0.29 | ||||
| Latvia | 4.67 | *** | 4.31 | *** | 0.29 | 0.38 | ||
| Malta | 1.31 | 0.95 | -0.28 | -0.08 | ||||
| Netherland | -0.22 | -0.36 | -0.48 | ** | -0.37 | * | ||
| Poland | 4.40 | *** | 3.96 | *** | 0.45 | 0.66 | ** | |
| Portugal | 1.63 | *** | 1.33 | * | -0.24 | -0.07 | ||
| Romania | 9.00 | *** | 8.86 | *** | 2.09 | *** | 2.11 | *** |
| Sweden | 0.26 | 0.25 | -0.71 | ** | -0.64 | ** | ||
| Slovenia | 2.42 | * | 2.00 | 0.22 | 0.40 | |||
| Slovakia | 5.52 | *** | 5.10 | *** | 1.35 | *** | 1.56 | *** |
| United Kingdom | -0.56 | * | -0.65 | * | -0.50 | *** | -0.45 | * |
| Dep. var.: ln(GDP per capita) | [1] | [2] | [3] | [4]
| ||||
| Germany (benchmark) | - | - | - | -
| ||||
| Austria | -0.76 | *** | -0.73 | *** | -0.37 | *** | -0.37 | *** |
| Belgium | -1.17 | *** | -1.17 | *** | -0.57 | *** | -0.60 | *** |
| Cyprus | 0.78 | -0.12 | 0.30 | 0.22 | ||||
| Spain | -1.11 | *** | -1.09 | *** | -0.46 | *** | -0.47 | *** |
| Estonia | 1.62 | *** | 1.67 | *** | 0.66 | ** | 0.32 | |
| Finland | 0.60 | *** | 0.71 | *** | 0.25 | 0.21 | ||
| France | -0.68 | *** | -0.65 | *** | -0.21 | ** | -0.21 | ** |
| Greece | 0.05 | 0.05 | 0.27 | ** | 0.21 | * | ||
| Ireland | -0.82 | ** | -0.87 | ** | -0.65 | ** | -0.48 | * |
| Italy | - 0.72 | - 0.72 | - 0.45 | *** | -0.41 | *** | ||
| Lithuania | 1.37 | *** | 1.56 | *** | 0.48 | *** | 0.25 | |
| Luxembourg | -0.54 | -0.62 | 0.31 | -0.39 | ||||
| Latvia | 1.45 | *** | 1.54 | *** | 0.44 | 0.19 | ||
| Malta | -0.31 | -0.29 | -0.33 | -0.37 | ||||
| Netherland | - 1.02 | *** | - 1.02 | *** | -0.63 | *** | -0.56 | *** |
| Portugal | -0.11 | -0.10 | -0.25 | * | -0.28 | * | ||
| Slovenia | -0.53 | -0.56 | * | -0.48 | * | -0.43 | * | |
| Slovakia | 0.62 | *** | 0.62 | *** | 0.20 | 0.12 | ||
| Dep. var.: ln(GDP per capita) | [1] | [2] | [3] | [4]
| ||||
ρ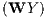 | 0.83 | *** | 0.85 | *** | 0.70 | *** | 0.68 | *** |
Φ1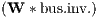 | 0.005 | *** | 0.008 | *** | 0.008 | *** | 0.005 | *** |
Φ2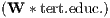 | - | - | 0.002 | *** | 0.002 | *** | ||
| Number of obs. | 2024 | 2024 | 2024 | 2024
| ||||
| R2 | 0.69 | 0.68 | 0.79 | 0.80
| ||||
| Log-likelihood | 1924 | 1935 | 2158 | 2152
| ||||
| DIRECT | ||||||||
| GDP per capita (initial) | 0.48 | *** | 0.50 | *** | 0.52 | *** | 0.49 | *** |
| Business investment | 0.008 | *** | 0.008 | *** | 0.006 | *** | 0.005 | *** |
| R&D expenditure (% of GDP) | 0.12 | *** | 0.12 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.02 | *** | 0.01 | *** | -
| ||
| Skilled migrants | - | - | - | 0.01 | *** | |||
| Long-term unemployment | - | - | -0.02 | *** | -0.02 | *** | ||
| Tertiary education | - | - | 0.004 | *** | 0.004 | *** | ||
| INDIRECT | ||||||||
| GDP per capita (initial) | 2.11 | *** | 2.38 | *** | 1.11 | *** | 0.94 | *** |
| Business investment | 0.06 | *** | 0.09 | *** | 0.04 | *** | 0.02 | *** |
| R&D expenditure (% of GDP) | 0.53 | *** | 0.58 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.08 | *** | 0.03 | *** | -
| ||
| Skilled migrants | - | - | - | 0.03 | *** | |||
| Long-term unemployment | - | - | -0.04 | *** | -0.04 | *** | ||
| Tertiary education | - | - | 0.01 | *** | 0.01 | *** | ||
| TOTAL | ||||||||
| GDP per capita (initial) | 2.59 | *** | 2.88 | *** | 1.64 | *** | 1.43 | *** |
| Business investment | 0.07 | *** | 0.09 | *** | 0.04 | *** | 0.03 | *** |
| R&D expenditure (% of GDP) | 0.65 | *** | 0.71 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.09 | *** | 0.05 | *** | -
| ||
| Skilled migrants | - | - | - | 0.04 | *** | |||
| Long-term unemployment | - | - | -0.05 | *** | -0.06 | *** | ||
| Tertiary education | - | - | 0.02 | *** | 0.02 | *** | ||
| Dep. var.: ln(GDP per capita) | [1] | [2] | [3] | [4]
| ||||
ρ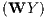 | 0.69 | *** | 0.70 | *** | 0.63 | *** | 0.58 | *** |
Φ1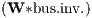 | 0.011 | *** | 0.012 | *** | 0.009 | *** | 0.009 | *** |
Φ2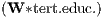 | - | - | 0.004 | *** | 0.003 | *** | ||
| Number of obs. | 1264 | 1264 | 1264 | 1264
| ||||
| R2 | 0.71 | 0.68 | 0.82 | 0.84
| ||||
| Log-likelihood | 1529 | 1530 | 1632 | 1644
| ||||
| DIRECT | ||||||||
| GDP per capita (initial) | 0.68 | *** | 0.69 | *** | 0.69 | *** | 0.63 | *** |
| Business investment | 0.007 | *** | 0.007 | *** | 0.006 | *** | 0.005 | *** |
| R&D expenditure (% of GDP) | 0.08 | *** | 0.08 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.005 | *** | 0.010 | *** | -
| ||
| Skilled migrants | - | - | - | 0.02 | *** | |||
| Long-term unemployment | - | - | -0.01 | *** | -0.01 | *** | ||
| Tertiary education | - | - | 0.003 | *** | 0.003 | *** | ||
| INDIRECT | ||||||||
| GDP per capita (initial) | 1.33 | *** | 1.42 | *** | 1.02 | *** | 0.77 | *** |
| Business investment | 0.05 | *** | 0.05 | *** | 0.03 | *** | 0.03 | *** |
| R&D expenditure (% of GDP) | 0.15 | *** | 0.16 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.01 | *** | 0.01 | *** | -
| ||
| Skilled migrants | - | - | - | 0.02 | *** | |||
| Long-term unemployment | - | - | -0.02 | *** | -0.02 | *** | ||
| Tertiary education | - | - | 0.01 | *** | 0.01 | *** | ||
| TOTAL | ||||||||
| GDP per capita (initial) | 2.01 | *** | 2.11 | *** | 1.71 | *** | 1.40 | *** |
| Business investment | 0.05 | *** | 0.06 | *** | 0.04 | *** | 0.03 | *** |
| R&D expenditure (% of GDP) | 0.23 | *** | 0.24 | *** | - | -
| ||
| Pop aged 15-34 | - | 0.01 | *** | 0.02 | *** | -
| ||
| Skilled migrants | - | - | - | 0.04 | *** | |||
| Long-term unemployment | - | - | -0.03 | *** | -0.03 | *** | ||
| Tertiary education | - | - | 0.02 | *** | 0.01 | *** | ||