Volume
3, Number 1, 2016, 87-104 journal homepage:
region.ersa.org
Volume
3, Number 1, 2016, 87-104 journal homepage:
region.ersa.orgDOI: 10.18335/region.v3i1.74
Population Structures in Russia: Optimality and Dependence on Parameters of Global Evolution*
1 University of Vienna, Vienna, Austria (email: yury.egorov@univie.ac.at) Received: 4 March 2015/Accepted: 22 June 2016Abstract. The paper is devoted to analytical investigation of the division of geographical space into urban and rural areas. A city has an attractive potential based on scale economies. For moderate scale effects optimal population of a city depends negatively on transport costs that are positively linked to energy price index. In the last 10 years we have observed substantial volatility of both food and energy prices at the world stock markets, and this puts pressure on spatial structures. If the shocks are fast and high, adaptation may be impossible and shock will persist. This took place during the early 1990s in the former USSR, where after transition to world price for oil in domestic markets existing spatial infrastructure became suboptimal and resulted in persistent crisis, leading to deterioration of both industry and agriculture. Russia is the largest country and thus has large resource endowment per capita, but it has too low population density. Due to large distances it might be optimal to reduce transport cost either by fuel subsidy or higher competition. This will work also against disintegration of the country.
JEL classification: R14, R23, R40, R48
Key words: urban, rural, population density, prices, transport, transition
1 Introduction
The world is evolving with time, with the change of population, GDP, energy consumption, price indices and other parameters. But spatial patterns are also changing: people migrate from rural to urban areas, cities grow and for some of them this growth seems to have no limit. The process of population and GDP growth is accompanied with urbanization. Hence, cities should have attractive potential. It has its origin in scale economies but congestion limits this process. So far, urbanization seems to be irreversible. But there might be conditions for return migration to rural areas.
Global evolution has different temporal scales. Any process can be decomposed into trend, cycle, and random components. The response of economy to temporal shocks has some typical duration. It can adjust to slow change, but fast change typically causes a crisis. Recently we observe both a positive trend and substantial volatility in the price indices for food and energy (see Figure 2). Is it easy to adapt to those fast changes? Figure A.1 (in the Appendix) shows that the perceived adaptation costs can be very high, comparable to adaptation to global warming. The negative impact of energy price volatility is perceived to be much higher than for other commodities and for consumer goods.
Economic theory typically studies spaceless economy, while regional science also accounts for spatial effects. Adding space to the model allows for the tracking of the location of buildings and people. Typically relocation of people as a response to shock is a much faster process than reconstruction of buildings.
When we analyze economic geography, we have to distinguish between infrastructures (buildings, roads and other human-made landscape change) and structures (location of people, occupation, etc). Contrary to other economic markets, where adjustment to equilibrium is often costless, change in infrastructure is very expensive, while population movement is also relatively expensive. That is why we should not expect much change in infrastructure in the short run, while structures (location of population) will react to price shocks earlier. While price change effects are substantial, they can be masked by other economic factors and by the frictions related to high cost of mobility. Besides that, there is uncertainty about shock persistence (that will limit mobility of a rational agent).
This paper tries to find out if changes in food and energy price indices can create such incentives for relocation in space. Russia is an important example because it has experienced a severe and persistent rise in the relative index of energy prices and transport costs during transition and was not able to fully adapt to it in the period of 20 years. It is also an important example because of its huge territory and low population density making the role of transport costs highly influential. This paper has two simple models deriving optimal location of population across rural and urban areas on one hand, and the optimal location and size of plants as the function of scale economies and transport costs on the other.
Reality is always more complex than the models, which is why it does not make sense to make models too mathematically complex. The goal is to explain real phenomena. Here the goal is to stress high vulnerability of spatial structures to the shock in transport costs that are linked to the shocks in the energy price index. Russia has experienced such shocks twice – in the 1990s, after transition from regulated price of gasoline to the world price, and today, when it is subject to the current oil price volatility. While the model assumes a representative agent and city of one type, a real shock in the energy price is also an income shock for oil exporting economies such as Russia. However, while a change in taxes might counterbalance the benefits from a lower oil price, it does not translate into lower domestic transport cost1 .
Some authors (Robert, Lennert 2010) argue that peak oil will also have a persistent negative shock on the economy, causing people to incur high costs in the short run and even higher costs to relocate to smaller cities in the long run. The Russian experience is important to keep in mind to understand what might happen then.
This article is mostly theoretical but also presents some stylized facts that are less known in regional science literature, especially about the evidence from Russia during the transition period. Most of the economic literature assumes equal access of all participants to the market. However, there is an asymmetry between them and it is related to transport costs. While there are many microeconomic studies about urban space, rural space is much less studied (although von Thünen has started its modelling already in 1826). The areas with low population density are especially important in the case of Russia, because high transport cost can even shut down some sorts of economic activities there.
The first goal of this article is to investigate the influence of changes in global price indices on spatial structures (city sizes and rural population density). Another goal is to explain recent changes in the population location and its activities in Russia, its connectivity, and to suggest policies that could improve those structures.
First, a simple model of optimal city size is suggested. The explicit dependence of population size in a city on energy prices is of special interest. The reason is that we have observed a positive trend of energy prices between 2000 and 2014. Moreover, if peak oil arrives, it will reinforce this tendency. The idea that optimal city size under peak oil should be smaller than now was already discussed in the literature; see Robert, Lennert (2010). Here this result will be obtained formally in the model of Section 3. Next, in Section 4, the optimal size of small farms for self-employed peasants is studied. The result depends not only on the country’s territory and population, but also on price indices for food and energy. Section 5 studies equilibrium between rural and urban areas and its sensitivity to future peak oil. Section 6 discusses to what extent price volatility can result in changes of spatial patterns of economic activity. The case of Russia in the 1990s is an important example investigated in Section 7. Some policies are also suggested. Section 8 concludes.
2 Literature Review
Classical regional science studies the question of optimal allocation of economic activity in space, and this paper is a contribution to this direction. Some assumptions are similar to those used in urban economics but some differ. The assumption of space continuity and two-dimensionality is crucial here. Contrary to many other papers, space plays a role not only for transport costs but also for modelling of land which is an important input to the agricultural production function.
There exist several trends in economic literature that address location choice and account for transport cost in economic modelling. Urban economics starts from the works of Alonso (1964) and many other authors, and focuses on commuting transport cost that drives land rent.
Central Business District model with inverse dependence of land rent to the distance to metropolitan center was suggested by Mills (1967) and later elaborated by many authors, including Fujita (1989). Henderson (1974) has studied optimal city size and elaborated general equilibrium model that explains variation of cities by size. There are many followers of his approach with different mathematical set up. Each city is a balance of agglomeration and congestion forces that results in some equilibrium.
The concept of the existence of a unique optimal city size obviously does not reflect reality and thus has been criticized by different authors. Richardson (1972) finds the attempt to equalize city size foolish, because the variety of optimal forms can exist. Capello, Camagni (2000) elaborated this idea and argue that the efficient city size depends on what it produces. They confirm the existence of economies of scale but only up to some level. Then structural readjustment and linkages with other cities (polycentric urban system) start to play their role.
Many authors address the issue of utility in cities. While high land rent increases the value of housing for sale, it is not translated into utility of a resident but rather has cost for him. Royuela, Surinach (2005) present an empirical study of utility of citizens in Barcelona. Their approach to optimal city size is based on the maximal difference between aggregate agglomeration advantage and location cost curves. Mascarilla-i Miro, Yegorov (2005) use the similar idea in theoretical form and derive the attractiveness of a city as the function of its population and studies the equilibrium split of population across cities.
Castells-Quintana (2015) empirically finds that urban concentration may not drive economic growth. This suggests that urban structures may react negatively to shocks. Yegorov (1999) studied the equilibrium mapping of the population with different income into dachas (small and standard plots of land with summer housing of controlled size) owned by many citizens in the USSR and the shock to this spatial infrastructure imposed by a shock in transport costs in Russia after transition.
Yegorov (2005, 2009) elaborates the concept of the economic role of population density. Rural population density can influence economic growth. There exists an optimal population density for resource based economies that in reality differ across countries depending on their individual characteristics. Too low of a population density gives high resource endowment per capita but there is a problem in building a sufficiently dense road network.
Spatial structures are sensitive to changes in economic parameters. Urban economics with its concept of central business district (CBD) derives equilibrium location of citizens as an interplay between location rent and transport cost. If transport costs grow, residents at the city periphery will suffer more and may have an incentive to migrate to other cities (if such an option exists). Such a scenario will be considered further, in Section 6.
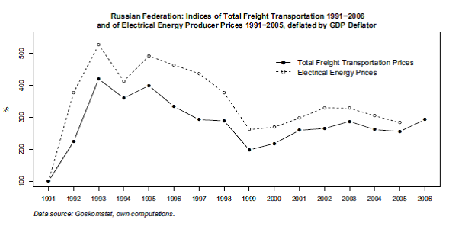
There are some studies about the influence of a shock in transport costs to both infrastructure and location of people. Russia is an important example because it has low population density and thus large distances covered by each citizen annually on average. Kauffmann (2007) documents the dynamics of the relative index of freight transport costs in Russia after transition, based on Goskomstat data. The ratio of transport costs to other costs jumped from 1 in 1991 (reference year) to 5 in 1992, then dropped slightly in 1994 but has never dropped below 3 between 1992 and 2005. Hence, it was not temporary but a permanent shock. There was a high correlation between those changes and electricity prices. Domestic prices for gasoline in Russia had a similar evolution after the move from domestic to world price for oil since 1993.
This shock was indeed important for freight, especially over long distances, but it was much less pronounced for the cost of using public transport in cities. While the relative change of those prices was of the same order, in the 1990s the personal transport bill in Russian cities was still affordable (contrary to negligible before 1991). However, the tickets from village to regional centers became prohibitively expensive.2
3 Simple Model of an Optimal City Size
While there exist many complex models of agglomeration, this article will deal with rather simple one. It is well known that historically cities were producing industrial goods, contrary to rural areas producing agriculture. However, in the last decades services started to dominate in the GDP of many countries. While they can be produced in all locations, the dominant share of services is still produced in cities. A city of larger size is characterized with larger population and higher variety of skills. Some services (like hospital, stadium and theater) require some minimal population threshold to start their activity. Thus, a larger city will have more variety of services and thus will produce a higher service GDP per capita. There are also scale economies for infrastructure cost (network of utilities, roads) in a city. They bring scale economies to industrial production. Since many economic activities in cities have scale economies, there is agglomeration force working in the direction of city growth. But at the same time there exists an opposite force coming from general congestion. A simple way to model it is to consider central business district model (CBD). For simplicity, radial symmetric city (of radius R) with a priori identical agents having land plots of equal size, b, is considered. Let H denote construction costs of a basic house (that does not depend on location).
It is assumed that the price of industrial and service output is normalized to one, while the price index for energy, E, and food (agricultural output), A, can vary.
The utility of an agent in a city with population N and radius R can be also viewed as city potential. While there exists literature on CBD (see, for example, Fujita 1989), the model employed here comes from Mascarilla-i Miro, Yegorov (2005), because it is mathematically simpler and also takes into account city attractiveness due to scale economies. This model is a mix of micro and macro approaches. Urban citizens live on quite limited territory and thus are engaged in production activities that require little amount of land: industry and services. At the same time living in a city gives some scale economies related to pooling skills, saving on infrastructure per capita and others (Mills 1967, Henderson 1974, Capello, Camagni 2000). Scale economies here are modeled in a simple way like nonlinear return to population size. Their microeconomic origin can include more investment, attracting talent, scale economies in pooling labor market, etc. At the same time, costs of living in a city are modeled in a way traditional for urban economics; the sum of rents plus commuting. This simple set up assumes constant land plot per capita in a city3 , abstracting from coexistence of multi-story buildings and different land endowments due to wealth differential. It can also be justified by the impossibility of fast change of the whole city plan as a reaction to price volatility. Thus, utility is postulated by the formula
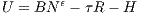 | (1) |
where ϵ > 0 is the scale factor and τ(E) denotes transport cost per unit of distance, that positively depends on energy price index, E. To make agents indifferent across locations in a city, the sum of transport costs to commute to CBD and rental price of a flat (sum of construction costs and location rent) should be constant. Assuming rental price at the edge of a city to be zero4 , we get τR + H = const, and this value represents cost index of living in a city. Since the territory of radially symmetric city equals to πR2 = Nb, where b denotes area occupied by a person, we can express U as the function of N:
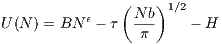 | (2) |
The optimal city size can be obtained by differentiation of (2) w.r.t. N, giving its optimal value:
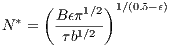
It is easy to show that the optimal city will be of finite size only for relatively small scale economies: 0 < ϵ < 1∕2. This model allows for the coexistence of cities of different sizes due to differences in scale economies (here parameter ϵ) for different productive activities but this is acceptable for our study.
Further we study the comparative statics. The partial derivatives for the optimal city size of type ϵ with respect to b and τ are both negative:
 | (3) |
For us it is important that growth in transport cost leads to decline in the optimal population of a city. For ϵ < 1∕2, optimal population size depends on ϵ positively. The richer the population, the larger land plot per capita, b, is demanded. This lowers the optimal population of a city in developed economies.
The role of transport costs is also important. While this is not explicitly accounted for, transportation time also influences utility. Technological development in transportation reduces it, and thus makes CBD accessible from larger distances; this makes city size larger. On the other hand, congestion in the form of traffic jams increases this time, and thus reduces the radius of optimal city.
Sinced 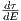 > 0, it can be concluded that the growth of energy prices leads to a decrease of
an optimal city size. Further we focus only on the case of ϵ < 1∕2, where finite equilibrium city
size exists.
> 0, it can be concluded that the growth of energy prices leads to a decrease of
an optimal city size. Further we focus only on the case of ϵ < 1∕2, where finite equilibrium city
size exists.
4 Optimal Agricultural Density
Rural population density has quite high variation across the globe, from 500 people per sq. km in fertile lands in India and China to less than 1 person per sq. km in rural Australia, Canada and Siberia. There is no unique equilibrium population density; it depends also on regional factors. However, the density in a particular region may be subject to shocks.
The model of this section is also highly stylized. Since rural land rent is typically much lower than urban, it was neglected in the model of a city, but is kept here. In the case of Russia is also can be neglected, but we keep it for generality.
The paper focuses on the role of population density, and it is accounted for in the model of optimal land plot for agriculture and finally utility of farmers. It is assumed that all land has equal square plots with the side r and hence size S = r2 and is owned by farmers. Depending on plot size, they can choose different cultures and technologies. For modeling agricultural density, consider a Cobb-Douglas production function in agriculture, based on labor (L) and land (S): Y = AL1-aSa, where A stands for the food price index. A farmer is assumed to supply inelastically one unit of labor and applies it to land plot. Substitution between land and labor is crucial. Depending on land plot size, a farmer can choose between different technologies. For the same value of output growing berries requires less land but more labor than wheat. There are decreasing returns to scale in agriculture to land plot size if only one farmer works there. At the same time, harvesting on a larger land plot involves higher transport cost (see Yegorov 2009). What are the main costs? There is land rent, R, and there are costs (like ploughing) that require energy input; both are proportional to land size S. There is also the cost of delivery to the market, which is proportional to the distance, d, to this market and unit distance transport cost, τ, which depends positively on energy price, E. Hence, the profit of a farmer is given by:
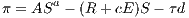 | (4) |
Profit maximization for equation (4) with respect to land size, S, leads to equation
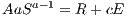 | (5) |
that gives optimal plot size, S*. In the case a = 1∕2, the expression for S* is very simple:
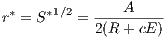 | (6) |
This optimal land plot for a farmer depends positively on the food price index and negatively on the land rent and energy price index:
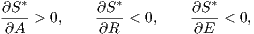 | (7) |
We can see from (7) that when food and energy prices change proportionally, we have opposite effects on optimal land plot and thus small overall effect. However, very often they change disproportionally and this can cause a negative effect on agriculture (especially when energy prices grow much faster than food prices).
If we have a fixed rural population, N, and all rural arable land Q is divided equally among them, then a plot per person is S = Q∕N. The corresponding rural population density is then ρ = N∕Q. Using formula (6), we can find optimal population density,
 | (8) |
Note that the signs of partial derivatives for optimal rural population density, given by (8), with respect to A, R and E are opposite to those given by (7). If ρ < ρ*, there is unused arable land and this can stimulate urban-rural migration. In the opposite case the rural area is overpopulated, and this drives urbanization.
We have a story in the spirit of von Thünen (1826), where farmers at larger distances from the city have to pay higher transport costs to bring good to the market but can enjoy a larger land plot. This story is only true when rural population density is low and not all arable land is developed. This is still the story of many regions in Russia, but cannot be applied for fertile and populated areas of China and India, where rural land plot depends on population density and may be smaller than its optimal size. In fact, in overpopulated rural areas this makes the profit of a farmer too low and stimulates migration to cities.
Suppose that the rural population density has an intermediate value, allowing all of those who want to do agriculture to select an optimal plot. Then land rent is no longer exogenous. The rise in food price will drive agricultural rent, and prevent the farmer from expanding the size of his plot. The fall in food price as well as the growth in energy prices will result is lowering optimal plot and can stimulate urban-rural migration but only if utility of living in a city also becomes lower. In other cases, farmers will prefer to develop only a fraction of land, saving on costs. Thus, a rise in energy prices will result in the decline of agricultural output for constant rural population. This effect is observed in Russia and will be discussed later.
Another important issue is related to the transport cost to access the market, the last term in equation (4). Here we have an important rural asymmetry between areas close to cities and areas more remote. In the second case, the cost of market access can be so high that agriculture will simply shut down being unable to produce profitably even at zero land rent. This may be a problem in the countries with low population density, like Russia. Another problem that can harm agriculture is no direct access of farmers to the market. A too high share captured by intermediaries in the final price for food can also make agriculture not profitable. One example from Russia was shown on TV in 2015: fishermen get only 30% of the final price for fish, transport cost is 10% and 60% goes to intermediaries.
4.1 Different Types of Equilibria
It is possible to construct a formal equilibrium in the full space, where all land is used. Assume that all space is occupied with agricultural and urban population, but urban density is much larger, so that we can neglect the territory occupied by cities5 . Let γ be the fraction of rural population, ρ the average density and ρa agricultural density. Then ρa = γρ. To make agents indifferent between living in a city or rural area, it is necessary to equate their utilities from both options: V 1 = U(N*) = U*. This leads to the transcendental equation
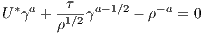 | (9) |
that can be reduced to a cubic equation for a = 3∕4 and y = γ1∕3. This equation (due to special property of signs) has a unique positive root. Thus, we can find optimal split of the population into urban and rural6 .
The equilibrium location structure includes “raisins" of optimal cities in a “cake" of uniformly dispersed agricultural population. For a given total population of a country, population density in cities, transport costs, coefficient of increasing returns in city and decreasing returns on agricultural land, there exist optimal number and size of cities and optimal agricultural density.
This type of equilibrium is relevant for densely populated countries, like India and China. If the price index for food grows, there are additional jobs on the farms because it becomes optimal to have more workers per 1 hectare. Sometimes employment may be informal, and that is why legal issues about land ownership are of less importance.
The situation in Russia is completely different. Here not all arable land is used today and the problem is also in high transport cost from remote farms to the market.
4.2 Model Summary
The summary of the results of those models can be formulated as a following proposition.
Proposition 1. There exist optimal size of cities and agricultural land plots developed by one farmer (gives scale economies and land productivity). They depend on global price indices for energy (given transportation technology) and food. Changes in those price indices make those structures suboptimal. In particular, growth in energy prices makes optimal city sizes and plots developed by one farmer smaller.
5 Spatial Urban-Rural Structure and Peak Oil
5.1 Equilibrium and Relocation Cost
In theory, such an equilibrium between urban and rural areas should exist and it should give the same utility for living in a city and working in manufacturing as it does for living in a rural area and working in agriculture (Yegorov 2006). Most of the time we observe disequilibrium, and it stimulates rural-urban migration. However, an energy price shock leads to decline in utility in cities due to high commuting costs.
Transition across equilibria is not costless. Let B denote annual benefit from either migration or building new infrastructure (comparing to current utility, B = U(n) - U(o), n: new, o: old) and C denote the fixed cost of such change. Let T denote the expected time span of current sub-optimality due to price shock. Then transition to new (infra)-structures will take place only if BT > C. Note that C is lower for migration than for rebuilding; it depends positively on interest rate.
In the short run no new buildings can be constructed, and citizens have two options: to suffer rising costs or to move to rural area. While richer household can afford staying, poorer can move to rural area, where commuting is cheaper. If the food price index grows faster than energy, they can engage in agricultural activity. Since optimal land plot there also becomes smaller, there might be land for them to work7 .
This effect is opposite to urbanization. In the history of Russia, it was observed two times. First, after the civil war of 1918-1920, industry was destroyed and cities lost scale effects attracting people. The second time was in the 1990s, after transition to a market economy accompanied by drop in GDP per capita. Many urban citizens had small land plots (dachas) and spent some time doing small agricultural activity.
5.2 Change in Energy Price Index
Since oil is an exhaustible resource, sooner or later its production will peak. Scientists have different opinion about this timing, but most of them agree that it will come in the first half of the 21st century. According to IEA data (see Figure 1), the discovered conventional oil fields have already peaked, and the hope is for yet undiscovered fields and non-conventional oil. Substitution of oil for renewable energies in transportation goes very slowly and thus peak oil can come unexpectedly causing very high rise in oil prices.
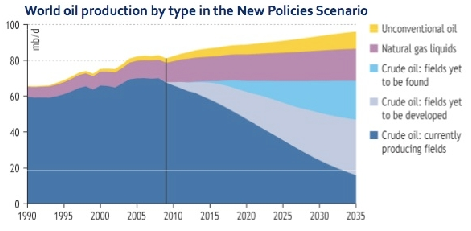
Source: The International Energy Agency’s (IEA) World Energy Outlook 2010
The paper of Robert, Lennert (2010) analyzes the impact of oil peaking for Europe. One of their results is that oil peaking will increase prices and reduce transportation, and this will restructure the whole urban system. In particular, sub-urbanization will be reversed and people will move to more compact cities.
Indeed, the result of Section 3 shows that the optimal city size declines with the rise in transport cost caused by the rise of energy (and in particular, oil) prices. Commuting inside large cities will become prohibitively expensive. Market forces will cause both migration to smaller cities (see Mascarilla-i Miro, Yegorov 2005) and the decline of land rent in a large city until new equilibrium will emerge.
In line with our model, the rise of oil prices will make the energy price index higher. This will make transportation (and harvesting) more expensive. In order to keep rural areas stable, there will be an upward push in the food price index. If the ratio of A∕τ remains constant, nothing happens with optimal rural density. That is why this shock will harm mostly urban population, and it will relocate from large to smaller cities. Since rapid construction of new smaller cities is hardly possible, in the short run there might be reverse, urban-rural migration.
6 Reaction of Spatial Patterns to Price Volatility
By spatial patterns we understand both infrastructures (buildings, etc.) and structures (location of population). Price variation over time (see Figure 2) can be decomposed into trend, cycle, and stochastic volatility of high frequency. While both prices of energy and food influence optimal location patterns, relatively high cost of mobility prevents reaction to changes of high frequency.
Note that change in price indices for energy and food is typically not driven by the changing demand (scale will then be modest) but by financial speculation. However, the cost of adapting to such changes is likely to be high (see Figure A.1 in Appendix), and comes mostly due to difficulty of adaptation of spatial patterns.
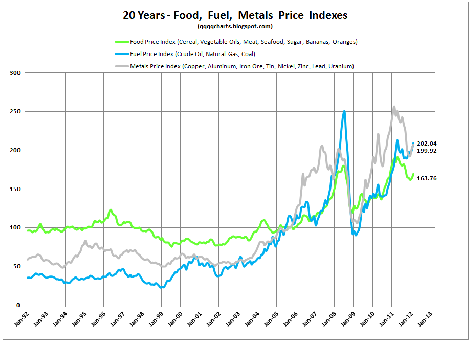
Source: http://qqqqcharts.blogspot.co.at/2012/03/20-years-food-fuel-metal-price-index.html
Trend component gives an incentive to change not only for population location, but also for infrastructures. City growth usually has a planned and random component, and reacts better to positive economic changes. If some spatial infrastructure becomes obsolete due to a bad price shock for its ecology (next section will show an example), it may be too costly to change it, even during a time horizon of 10-20 years.
As we know from business cycle literature, population reacts to business cycles by spatial and occupation mobility. That is why we can expect some rural-urban (or even reverse) migration as a reaction to both trend and cycle in prices for food and energy.
When we have co-movement in food and energy prices, we can expect little reaction of agriculture (because production there depends positively on food prices, but negatively on energy). On the other hand, urban utility is negatively affected by growth of the price indices in both energy and food, and such positive co-movement can be a big shock for cities, especially in less developed economies where food and transport represent a very high fraction of household expenditures.
The following testable hypothesis can be formulated.
Hypothesis: We can observe some changes in spatial structures only in the following cases: a) transition is slow, so that only new construction will take into account the existing price trend, while old infrastructures will not adjust, b) transition is fast (like peak oil) but is irreversible (T →∞, so that change is better at any cost, and c) adaptation cost is low comparing to benefits during expected shock duration, T.
Price volatility has a negative effect on the economy, because adaptation is costly and often not feasible. Not only trends and cycles in global prices for oil and food matter, but also a country’s laws regarding subsidies and taxes. The positive trend in oil price in the 21st century deteriorated utility in cities, but in the EU it was less pronounced, because the main component of gasoline price is tax. In a similar manner, a drop in oil prices in 2014-2015 gave less additional utility to citizens and farmers of EU, comparing to countries with low taxes. Some oil producing countries have a domestic price for gasoline well below the global price. This eases agricultural activity but elimination of such subsidies will put their infrastructures under shock. This happened in Russia during transition to a market economy, and this case will be considered in more detail.
7 Russian Changes in Prices, Structures, and Policies
There have been many changes in Russia after transition to a market economy in 1992. Since there was no free market before 1992 and prices have been set using administrative methods, economists often do not even compare those periods. However, wages and prices existed in both periods as well as free mobility, and thus people could choose their location optimally in both periods.
There are several factors that influence the decisions of the Russian population. Too high transport cost and high wage in Moscow (driven just by location of financial flows, exogenous to this model) have stimulated migration there. At the same time, urbanization level did not grow after 1992 and many people were actually living in rural areas to survive.
Two effects are especially important: a) existence of optimal spatial infrastructures before transition (Subsection 7.1) and b) the persistent shock in energy prices (7.2).
7.1 Optimal Plant Size as the Balance between Scale Economies and Transport Cost
In Soviet time, many giant plants were built, also because of scale economies. If we consider some scale economies in manufacturing that are balanced by the transport costs for the spatial area where inputs are harvested and the final good is distributed, we have mathematical model similar to one considered in the Section 3 (it is fully described in Yegorov (2009) but is given here shortly). Consider an optimal planner problem to invest fixed capital, K, into some industry and to choose a number of plants with scale economies (c > 0) that collect resources and sell the output at the uniformly populated territory around them. In this case the average distance of transportation is proportional to inverse square root of N. Formally, the problem is to maximize the benefits proportional to the total output minus cost of capital and transport:
![[ ( )1+c ]
max AN K- - τN -0.5 - γK
N N](7418x.png) | (10) |
After optimization we get the optimal number of plants to be proportional to the square of transport cost. The lower this transport cost, τ, the larger will be the size of optimal plant and the lower will be their quantity N, and this was the case of the USSR with its subsidized transport. So, if it was necessary to produce some output Y of particular good to satisfy the demand of the USSR (which was to some extent a closed economy8 ) given the price of output, A (also fixed), it was indeed optimal to build few super-giant plants, say 10, at the distance of about 1000 km from each other.
Now it is documented, that the (inverse) price ratio τ∕A, has increased by factor 3-4 during the transition and persistently stayed at this level thereafter (see Figure 3). This means that spatial industrial infrastructure of Russia is under persistent price shock since the 1990s. Under new conditions it would be optimal to have smaller plants with smaller market areas around. Especially this is important for cheap goods (like cement, wood, etc.) for which freight has a substantial fraction of the total price. Since rebuilding of all industrial infrastructures (just to change locations and capacity) is too high of an investment for any country, it can be done only in the very long run. Meanwhile, plants remain unprofitable. Only transport subsidies (at least partial) could have kept those industries alive, but this has not been done. The bankruptcy level in the non-extracting industries in Russia in the 1990s was very high. Nowadays there is neither a transport subsidy policy nor planned investment to rebuild this infrastructure on a new optimal level. Due to high transport costs not only has interaction between regions declined (both as trade and passenger trips) but there was also extensive migration to giant urban areas, especially to Moscow. While congestion factors in Moscow are high, the negative pushing effects from regions of Russia dominate.
7.2 Russian Transition Shock and Impact on Relative Price of Energy
Availability of cheap transport is very important for economic success of a country. Stratfor9 has proved that the economic success of the USA was highly determined by the presence of Mississippi river basin, with both cheap water transport and one of the largest global basins of arable land. In the case of such large territory with dispersed population like Russia cheap transport becomes crucially important. The Volga River basin (smaller than Mississippi but still the largest in Europe) gave high growth potential in the 19th century, but the development of railroads was needed for the connection with other (especially Asian) river basins. While rail transport is about twice as expensive as river (see the reference to Stratfor’s article above), it allows to connect all points in a network, although at higher price. In the time of the USSR transport had been subsidized (the country kept domestic prices of gasoline and electricity at regulated level, below the world price), and this allowed for the integration of Siberia into an economic zone at the higher scale than similar territories in Canada.
Transition in Russia has caused substantial growth in relative energy and transport prices (see Figure 3). This caused a shock for agriculture, and it went into gradual decline (see Table 1). For whatever reason10 , Russian agriculture could not benefit from the rise in the food price index. However, this was also a shock for industry. The urban population has experienced both shocks (transport and food) and their utility has declined in the 1990s. Many people were using dachas (small land plots of about 0.1 hectare given to citizens in Soviet time for symbolic price) to help family budget by small crops, but this was mainly an autarky (self-consumption) due to high transport costs and small volumes.
| Urban | Price of | GDP per | Agriculture
| |
| Year | population | gasoline, | capita, | share of GDP,
|
| share,% | USD | USD | %
| |
| 1990 | 73 | < 0.1* | 3485 | 16.6 |
| 1995 | 73 | 0.35 | 2665 | 7.2 |
| 2000 | 73 | 0.33 | 1771 | 6.4 |
| 2005 | 73 | 0.66 | 5323 | 5.0 |
| 2010 | 74 | 0.84 | 10675 | 3.9 |
* Exact value is not available due to multiplicity of exchange rates before 1992
Not all evidence about the decline of agriculture in Russia is provided by official statistics. Academician V. Kashin writes that after transition, the quantity of labor force in agriculture has declined from 6 million to only 1.17 million in 2015. About 5 million people are officially unemployed but work on small land plots for personal consumption manually without machines. While their productivity is about 1/8 of one in the EU, they still produce about half of meat and milk and about 90% of vegetables11 .
7.3 Too Low Rural Population Density in Russia
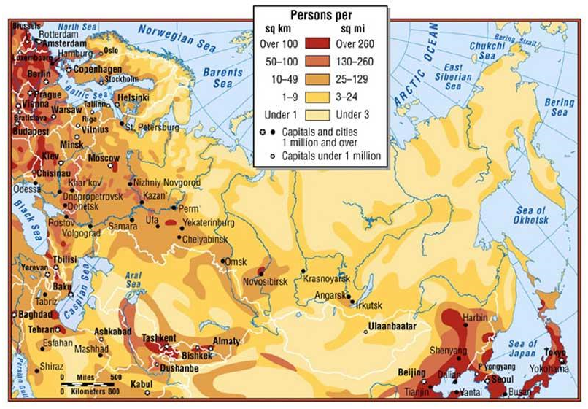
Source: http://www.roebuckclasses.com/maps/placemap/russia/russiapop.JPG
The difference between Russia and other countries is in its low population density (see Figure 4). This may have positive and negative effects (see Yegorov 2009). On the positive side, there is high land endowment per capita, allowing the harvesting of more mineral resources and the production of more agriculture. On the negative side, the population is too low to build a dense road network, and still declines. Also, low agricultural productivity in most Siberian areas leads to larger territory needed to produce the same quantity of output. Hence, the fraction of energy cost in agricultural output becomes higher. This poses a persistent problem for regional and rural development in Russia.
Figure 5 shows the global railroad map. Russia has many km of railroads, but their density even in the European part is below that in Western Europe, while the Siberian part has only the Trans-Siberian railroad (built in 1916) with only few secondary roads without any dense network. Absence of a dense road network (paved roads in Siberia are also not frequent) leads to low access to remote resources and the necessity to transport them without roads. This exercise is prohibitively expensive. Yegorov (2005, 2009) has shown that too low population density can be an obstacle for extensive and profitable land exploitation, and also can harm economic growth. Population growth in rural areas in this case might be a positive externality causing growth in productivity.
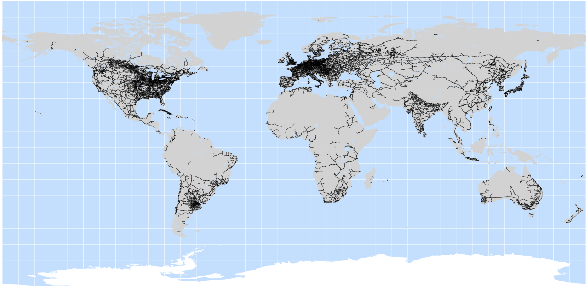
Source: http://bioval.jrc.ec.europa.eu/products/gam/images/large/railways.png
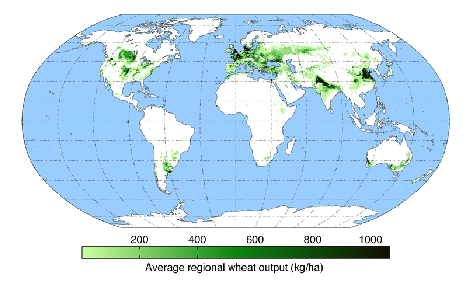
Source: http://en.wikipedia.org/wiki/File:WheatYield.png
Another problem in Russia is relatively low land fertility. In most of its regions (apart from North Caucasus), the yield of wheat is lower than in Western Europe (see Figure 6). While the USSR was the major global producer of wheat, Russian position today (as well as Ukrainian) is much lower. In 2012, Russia produced only 37.7 mill. tons of wheat and occupied the 6th position in the world12 , after EU (134.5), China (125.6), India (94.9), USA (61.8) and France (40.3). Thus, Russia does not use its territory efficiently. USSR had much higher agricultural potential. Wheat was produced not only for bread, but also for feeding animals. Now Russia imports a high fraction of consumed meat. China might require import of food in future, and this could be alternative source of income for Russia, when oil production will decline.
7.4 Disintegration of Russian Air Traffic and Threat for Integration
Air transport plays high role for the passenger transport. In the USSR the air transport was well developed. Labor policy has moved population over vast territory, and high demand for connection and cheap (subsidized) gasoline had driven up the market for air transport. After the dissolution of the USSR in 1991 and market reforms it went into deep decline and started to recover only after 1999 (see Figure 7).
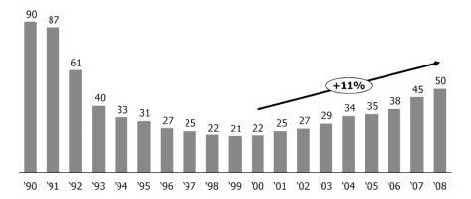
Lukjanov (2008) presents the following data. The quantity of air passengers continued to decline between 1996 and 1999 (from 26.96 to 21.47 million) and started to grow only afterwards. The decline after dissolution of the USSR has been much more substantial: in 1990 there were 90.8 million air passengers13 . Contrary to foreign air companies, the cost of fuel is the main cost component in Russia. For example, in 2006 Russian air companies spent 40% of their costs on fuel, comparing to only 12% for Delta Airlines. Savelev (2010) shows that between 2002 and 2007, the price of air fuel in Russia grew by 160%, while the ticket price by only 120%. This shows that fuel price is the main driver of transport cost for air passengers in Russia.
Table 2 shows that the topology of air traffic has changed. Now most of the regions are connected only with Moscow, while in the USSR they were connected between themselves.
| Direction of flight | 1990 | 2012 | ||
| To/from Moscow | 26% | 75% | ||
| Regional airlines | 46% | 22% | ||
| Local airlines | 28% | 3% | ||
There are two major microeconomic reasons for those changes. The first is substantial increase of relative transport cost in Russia after economic reforms of 1992: it was a shock of about 450% relative price rise in 1992, but the ratio stabilized at about 250% after 2000 (see Figure 3). The second is in higher income disparity. While in the USSR the ratio of income of the top 10% to the bottom 10% was only 3.5 (Atkinson, Micklewright 1992), after transition it has grown to 15 and remains at this level for many years. Hence, air transport became non-affordable for the majority of the Russian population. Demand shrinkage was especially pronounced among regions, where operation of even one air plane became non-profitable and thus was cancelled. This poses a threat for Russian regional integration.
Today the quantity of air passengers has increased, although not to the level of the USSR. Domestic air transport is still expensive and not affordable for a large fraction of the population. There is low competition across Russian airlines, while western low cost companies (like Ryan Air, Euro Wings) are not coming to Russian cities apart from Moscow. Low cost flights are almost unknown among Russian air companies. They may prefer to satisfy demand of richer populations and sell few expensive tickets because income distribution in Russia today is more unequal compared to the EU.
7.5 Optimal Policies for Russia
We see that Russia is facing persistent structural shock that was imposed by the growth in energy and transport prices. At present, Russia does not extract benefits from its large territory. It was an asset in Soviet time, but now became a liability.
Table 1 shows that the share of urban population in Russia was pretty stable during the last 25 years, while there were substantial changes in the domestic gasoline price and GDP per capita (also driven by oil price volatility), while the share of agriculture in GDP was declining. This shows that the place to live has some inertia and is not subject to influence of even long term trends. However, suppression of agriculture and the end of urbanization may also reflect structural changes in transport cost. High mobility costs could be the reason of the stabilization in the shares of urban and rural population. Only Moscow is growing because of higher attractive potential that has external origin to this model (financial center offering higher wages).
We see also a decline in agriculture despite high endowment of land (also arable) per capita. Its initial decline in the 1990s could also be due to the shock in transport costs that had suppressed agriculture in the areas distant from the major cities. But its decline after 2000 when GDP per capita was growing may also reflect mismanagement.
When all of the population tend to live in cities, it does not matter how large is the rural territory. For the efficient exploitation of rural resources the policy to reverse rural-urban migration should be used. Russia should use its agricultural potential more efficiently. Now it specializes on harvesting of only non-renewable resources (oil, gas, metals) but should specialize on renewable too (agriculture, forest and fishing).
One of the policies is to return to domestic subsidy of gasoline. Fuel for agriculture and large distance transport of agricultural goods may be subsidized. Many oil producing countries still have it, although this is not an efficient use of resources. At least, gasoline should be produced competitively (any cartel agreement should be eliminated) and there should be no tax on it. Another possibility is to increase competition in transportation to make its prices below the world level. Russia can also use the current drop in oil prices to boost domestic transportation, oriented not only on harvesting remote renewable natural resources but also on increase in passenger flow. This can also prevent Russian disintegration.
8 Conclusions
The paper studies the question of sensitivity of spatial location of the population to the changes in energy and food price indices. It consists of mathematical and policy parts. First, a simple theoretical model based on attractive potential of a city and cost-benefit analysis of a farm is considered. It results in finding an optimal city size and rural population density parametrically depending on transport costs.
The obtained results are further analyzed from the perspective of their sensitivity to external shocks in basic prices, like world food and energy price indices. It was shown that a rise of energy and food price alone requires change of the whole spatial pattern, which is too costly and painful. That is why peak oil might have very negative consequences for the global city network, requiring relocation and construction of new smaller cities. If food price (as return to producer) grows slower than energy prices, this causes rural shock and leads to rural-urban migration, resulting in lower rural population density than is optimal for this case.
The case of Russian transition is considered as an example of a severe shock in energy prices. It is a persistent shock for all industrial infrastructures that has resulted from a 3-fold increase in freight cost and then perturbed the whole spatial infrastructure that had been created mostly in Soviet time for subsidized transport costs. Higher transport costs (relative to composite good) in Russia after liberalization in the 1990s had several adverse effects for the economy and population. Too high transport costs made exploitation of natural resources and agriculture less profitable, especially in the areas with low population density. Overall urbanization level did not change, but it can be the effect of too high mobility cost. People migrate to large cities (the only source of attractive wages) but industry in other cities is depressed. Rural population density in Russia became even smaller because of a negative population growth rate, especially in the 1990s. All those effects contribute to a persistent negative shock for Russian economy which is one of the reasons for its crisis today.
The shocks to spatial infrastructure in Russia were not analyzed when transition policy was elaborated. Too high interest rate also works against adaptation to new environment. Now those issues have to be taken into account.
It is also important to understand that high energy price volatility poses a problem to global spatial structures. Models from this paper help to understand potential adjustments and the scale of corresponding costs.
References
Alonso W (1964) Location and land use. Toward a general theory of land rent. Harvard University Press, Cambridge, Mass. CrossRef.
Atkinson AB, Micklewright J (1992) Economic Transformation in Eastern Europe and the Distribution of Income. Cambridge University Press, Cambridge
Capello R, Camagni R (2000) Beyond optimal city size: An evaluation of alternative urban growth patterns. Urban Studies 37: 1479–1496. CrossRef.
Castells-Quintana D (2015) Malthus living in a slum: Urban concentration, infrastructures and economic growth. Journal of Urban Economics. CrossRef.
Fujita M (1989) Urban Economic Theory. Land Use and City Size. Cambridge Univ. Press, Cambridge. CrossRef.
Henderson JV (1974) The sizes and types of cities. American Economic Review 64: 640–656
Kauffmann A (2007) Transport costs and the size of cities: the case of Russia. University of Potsdam, discussion paper nr. 93
Koroteeva KP (2015) Statistical analysis of domestic air traffic in Russia. Magister thesis, moscow, higher school of economics (in Russian)
Lukjanov SA (2008) The market of passenger air traffic. modern state in Russia and CIS countries (in Russian). on-line: http://ecotrends.ru/images/Journals/2000-2009/2008/N10/3_Articles/006_%D0%9B%D1%83%D0%BA%D1%8C%D1%8F%D0%BD%D0%BE%D0%B2_2008_10.pdf
Mascarilla-i Miro O, Yegorov Y (2005) Modelling functional area and commuting flows. Cuadernos de Economia 28: 39–56
Mills ES (1967) An aggregative model of resource allocation in a metropolitan area. The American Economic Review 57: 197–210
Richardson H (1972) Optimality in city size, systems of cities and urban policy: a sceptic’s view. Urban Studies 9: 29–48. CrossRef.
Robert J, Lennert M (2010) Two scenarios for Europe: "Europe confronted with high energy prices" or "Europe after oil peaking". Futures. CrossRef.
Royuela V, Surinach J (2005) Quality of life and urban size. ERSA 2005 conference paper
Savelev D (2010) Analysis of russian market of passenger air (in Russian). http://cyberleninka.ru/article/n/analiz-rossiyskogo-rynka-passazhirskih-aviaperevozok
von Thünen J (1826) Isolated state. Pergamon Press. (English translation, 1966)
Yegorov Y (1999) Dacha pricing in Russia: General equilibrium model of location. CASE-CEU working paper no. 18, Warsaw
Yegorov Y (2005) Role of density and field in spatial economics. In: Yee L (ed), Contemporary Issues in Urban and Regional Economics. Nova Science Publishers, NY, 55–78
Yegorov Y (2006) Emergence and evolution of heterogeneous spatial patterns. ERSA congress 2006, Volos, Greece (http://www-sre.wu-wien.ac.at/ersa/ersaconfs/ersa06/papers/690.pdf)
Yegorov Y (2009) Socio-economic influences of population density. Chinese Business Review 8: 1–12
Yegorov Y (2011) Potential and spatial structure of population. ERSA congress 2011, Barcelona, Spain (http://www-sre.wu.ac.at/ersa/ersaconfs/ersa11/e110830aFinal00109.pdf)
A Appendix

Source: http://peakoil.com/forums/doomer-risk-perception-chart-t60660.html