Volume
2, Number 1, 2015, 33–53 journal homepage:
region.ersa.org
Volume
2, Number 1, 2015, 33–53 journal homepage:
region.ersa.orgAgglomeration effects on labor productivity: An assessment with microdata*
1 Institute for Employment Research (IAB) and Otto-Friedrich-University of Bamberg, Nuremburg, Germany (email: stephan.brunow@iab.de)2 Institute for Employment Research (IAB) and Otto-Friedrich-University of Bamberg, Nuremburg, Germany (email: uwe.blien@iab.de) Received: 11 July 2014/Accepted: 16 March 2015
*This research is part of the NORFACE research program on migration (Migrant Diversity and Regional Disparity in Europe – MIDI-REDIE project). The authors gratefully acknowledge the many ideas and comments they have received in this context at the ERSA, GfR and NARSC conferences and at the AQR-Workshop 2013 in Barcelona, especially by the NORFACE team colleagues Thomas de Graaf, Peter Nijkamp, Jacques Poot, and by many others. The responsibility for the analysis and the results remains completely with the authors.
Abstract. Urbanization and localization effects are known to boost the regional economy and its growth potential. The emergence of these effects is due to localized knowledge flows, the closeness to markets, and the diversity of services and industries. Urbanization and localization effects have the potential to increase the productivity (and profitability) of firms. While many studies have been conducted at the industry or regional level, this paper adds to the existing literature by starting at decisive economic actors level, i.e., at the level of individual business establishments, and accounting for the interaction with the surrounding regions. Based on a thoroughly constructed theoretical model, the empirical analysis involves exploiting an exceptionally large establishment panel study and Germany’s employment statistics. The empirical analyses use two-step regressions to separate establishments’ characteristics from regional influences. The empirical results obtained indicate that agglomeration effects are present. Because localization and urbanization forces are both important for individual establishments, the metropolitan areas are the main engines of labor productivity in the country.
Key words: Region, labor productivity, agglomeration effects, MAR effects, Jacobs effects
1 Introduction
Urbanization and localization effects have the potential to boost the regional economy and its growth (Henderson 2003, Combes, Gobillon 2014, Rosenthal, Strange 2004). The emergence of these effects is due to localized knowledge flows (Glaeser et al. 2011), the closeness to markets (Krugman 1991), and the diversity of services and industries (Jacobs 1969).
This paper concentrates on agglomeration effects on firms’ labor productivity because it is widely accepted that the dynamics of an economy depend strongly on this central influence. Metropolitan areas are the regions where innovations occur, and from these areas, innovations spread out nationally or even internationally. Since Marshall’s 1920 book (Marshall 1920) on economic theory, arguments have progressed that relate agglomeration effects to the performance of firms. Duranton and Puga’s modern typology shows that sharing, matching, and learning effects increase the productivity in metropolitan areas in particular (Duranton, Puga 2004). In the context of regionally diverse labor markets characterized by a broad variety of skills in a complex production process, we go beyond measuring human capital based on educational attainment. Instead, we introduce a task-based concept of educational investment to control for over- and under-education and for the complexity of jobs in business establishments’ production (Duncan, Hoffmann 1981, Autor et al. 2003). With “business establishment,” this refers to an individual plant of a firm, whose purpose is the production of goods or services.
We intend to observe the empirics of productivity more closely to link regional differences to agglomeration effects. Although many studies have been conducted concerning agglomeration effects, thorough analyses with microdata are still rare (see the overview of Combes, Gobillon 2014), especially from the perspective of individual firms. Analyses with microdata are required, however, to decide whether the assumed effects of agglomerations are critical for individual firms’ decisions, as these firms are the most important actors in the regional economy. The production process is organized within establishments. Aggregation could mask the crucial relationships between cause and effect or could produce an ecological fallacy (Duque et al. 2006) if a connection between variables found at the aggregate level is erroneously transferred to the individual-level. Among the few examples of empirical studies using microdata are Baldwin et al. (2010) and Drucker, Feser (2012).
This paper addresses the gap in microdata analysis by examining regional (intra-industrial) agglomeration economies, which may influence labor productivity, with microdata from an exceptionally large establishment panel study and from the employment statistics of Germany. This paper’s intention is to investigate the interaction between productivity and the regional economy to observe whether agglomeration effects matter. The available microdata are integrated into a linked employer-employee panel data set, which facilitates the analysis that is carried out in several steps.
The empirical study’s design is chosen to overcome certain difficulties: Standard methods of panel analysis are not appropriate to answer the question at hand because agglomeration forces vary relatively slowly. Therefore, we need to modify these standard approaches because we are interested in identifying and measuring agglomeration effects. The chosen approach has the advantage that it allows for studying effects at various levels of observation. It also takes the interaction of establishments, industries, and regions into account. This requires detailed measurements of the performance and mechanics of establishments or plants. It is necessary to control for several variables at this level in order to identify the interaction with the local economy’s properties. In terms of the regions, we are able to use relatively small units: In Germany, there are 412 districts (“Kreise” – NUTS3 regions), of which 411 are represented in our data. For the effects of larger regional units, we use spatially lagged variables generated by distance matrices.
In the following sections, we start with a brief outline of a theoretical model, which is used to derive an identification strategy. The inspiration for the empirical analyses’ design is from the two-step approach used by Bell et al. (2002). Next, we give an outline of the rich data source we use. Finally, we report the empirical analyses before concluding.
2 A theoretical model as the basis of the empirical approach
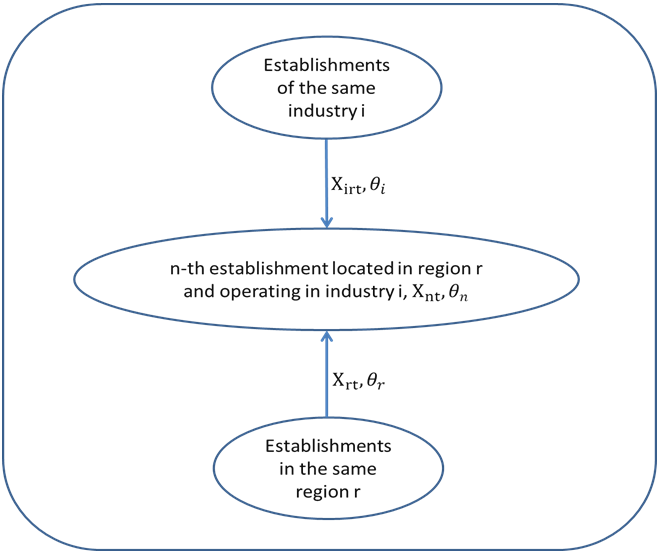
The theoretical model, which we use to derive an empirical approach, starts from a general characterization of the production process by an extended constant elasticity of substitution production function (CES function), which includes other common functions such as the Cobb-Douglas function as special cases. Under the assumption of profit maximization, we derive labor demand from the CES function. Using few simplifications allows for the development of a general empirical approach to estimate labor productivity, which also depends on the level of intermediate products. In our case, it is important that productivity depends both on the properties of the respective firms, and on the characteristics of the regions where the firms are located. Figure 1 provides a brief overview of the different levels that may influence establishment productivity.
2.1 Production technology
We assume a general functional form of an establishment’s production by specifying a CES function, given by
![[ ]-σ-
Y = α (AL )σ-σ1+ β(BK )σ-σ1 +γ (I)σ-σ1 σ-1](24-new5x.png) | (1) |
Total production Y is produced with labor L, capital K, and intermediate inputs I, where α, β and γ are parameters that describe the input shares of these inputs. The elasticity of substitution between the inputs is described by σ. For σ = 1, the production function becomes a Cobb-Douglas type. A and B relate to labor and capital productivity, respectively. The CES function is of a generalized form because output depends not only on labor and the capital stock, but also on intermediate products.
As frequently discussed in the literature, the productivity parameters A and B are assumed to be influenced by agglomeration effects: Being located in an agglomeration region yields additional benefits that increase output for a given level of inputs. We implement these agglomeration effects in the following Subsection 2.2. For level of sales E = pY , factor prices w for wages, R for the interest rate, and pI for the price of the intermediates, the compensated factor demand for labor is given by
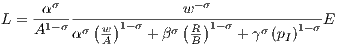 | (2) |
A firm’s labor demand increases with its level of sales, but decreases with wages and with labor productivity. This is expressed by A for 0 ≤ σ ≤ 1 when labor and other inputs are complementary to some degree. Additionally, the capital productivity parameter B affects labor demand. An increase in B yields an increase in labor demand when capital and labor are to some degree complements, whereas an increase in B yields a decrease in labor demand when capital and labor are to some degree substitutes. The level of sales divided by employment levels is a good proxy for a firm’s labor productivity; thus, rearranging (2) yields
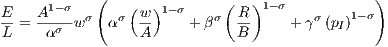 | (3) |
2.2 Productivity parameters and introduction of agglomeration effects
Labor productivity A and the productivity of capital B of Equation (3) are functions of establishment characteristics, which are observable Xnt and unobservable θn. According to agglomeration literature, productivity is further affected by influences emerging at a “higher” level of the hierarchy, such as the industry and the region (Moretti 2004). We therefore hypothesize that a firm’s productivity operating in industry i, which is located in region r and observed at time t, is influenced by an industry-specific regional effect θirt and a region-specific effect θrt, which may change over time (Combes et al. 2004). Collecting terms and assuming an additive coherence nested in an exponential expression yields
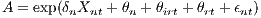 | (4) |
where some similar expression holds for B. The coefficient δn refers to the impact of establishment characteristics on productivity. As was the case with establishment-specific characteristics, θirt and θrt can be described by an observable and unobservable part, respectively. Xirt and Xrt are vectors of industry-specific regional variables and region-specific variables, which influence industrial and regional productivity, respectively. θr and θi refer to yet unexplained regional and industry effects. This leads to
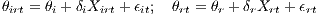 | (5) |
with δr and δi parameters that describe the change in productivity at the higher level. Substituting both expressions of (5) into (4) provides the agglomeration effects with augmented establishment productivity measures:
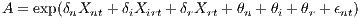 | (6) |
where some similar expression holds for B. The effects θi and θr also take over the interest cost, which may be specific for a special industry and region.
2.3 The augmented productivity model
Equation (3) describes a productivity measure – revenues per employee – from a theoretical perspective. Productivity depends on labor productivity and wages, but also on the price of capital, capital productivity, and intermediates. Labor productivity depends on establishment characteristics and characteristics found at a higher level of the hierarchy, as indicated in Equation (6). This equation can be substituted into (3). Ultimately, taking logs provides an augmented empirical specification, which approximates the theoretical model. With a new set of parameters γ, it reads as
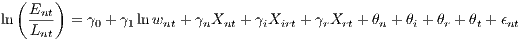 | (7) |
Unobserved time fixed effects are captured by θt, whereas ϵnt relates to an unexplained IID error term. In the next section, we discuss the estimation issues of the models presented in Equation (7).
3 Empirical model and identification strategy
From Equation (7), two empirical equations can be formulated, which integrate a different number of variables.
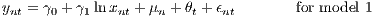 | (8) |
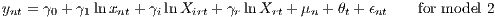 | (9) |
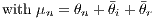 | (10) |
ynt is the log of sales per employee. The set of xnt includes all variables that are associated with the nth establishment during period t. This might include time constant variables. Accordingly, Xirt and Xrt relate to sets of variables for the industry and regional level, respectively. The θ parameters are as described above, and μn is a composite establishment-specific fixed effect, which also captures capital cost. It would be possible to use random effects instead of fixed effects and apply a multilevel model. However, using random effects requires an important additional assumption (which is often not observed): The random effects should be independent of the exogenous variables. Because this assumption is not required with fixed effects (FE), we use these. FEs are also able to take the multilevel structure into account, which is important for our problem.
The estimation strategy is inspired by the approach of Bell et al. (2002), which was suggested in turn by Card (1995). This is a two-step approach, which starts with an analysis of observations at the individual-level (workers for Bell et al. 2002, and establishments in our case). In a second step, we analyze the variation between regions (and possibly periods). In the first step, we control for the many influences on productivity, which are establishment-specific. The regional and intra-industrial averages, r and i, respectively, included in the establishment fixed effects μn, are then used in the second step to identify agglomeration effects and effects of other region-specific variables. It is not possible to integrate both steps into one because some of the variables characterizing a region do not vary in time and thus drop out in a fixed effects approach. Therefore, the two-step approach is required to control for the unobserved properties of establishments.
Considering a regression of Equation (8) that includes establishment fixed effects does not take into account the time-varying part of the regional and industrial variables, it is included in the error term. Additionally, the estimates of nearly time invariant establishment-specific factors are identified with only a few observations, when a change in variables occurs. Hence, much of the between-establishment variation is included in the fixed effects and for the time-varying variables in the remaining error term. The advantage of the estimation of (9) by means of establishment fixed effects takes the time variation of region- and industry-specific variables into account, and is no longer included in the error term. Insofar as these variables vary only slowly, their estimation is not precise in the first-step regression (Plümper, Troeger 2007, Greene 2011).
The region- and industry-specific variables Xrt and Xirt are included in (9) because a regression of (8) including establishment fixed effects yields biased results when variables of Xnt correlate with the time-variant part of Xirt or Xrt. If the mentioned correlation is negligible, the difference in estimates between (8) and (9) is expected to be small. In this case, the additional variables included in (9) are expected to be insignificant. Additionally, in both cases, the estimated μn for the second-step regression are expected to be quite similar.
The fixed effects estimation at the establishment level offers one further advantage compared to a pooled regression, as sorting establishments into different regions might bias the results when between-establishment characteristics are used to identify parameters. Put differently, more productive establishments might be located in different regions compared to less productive establishments. If exporting establishments are located in regions where relatively more productive establishments are present, there is a bias in the estimate for exports because of the selectivity problem (Baldwin, Okubo 2006).
According to the above argumentation and according to Bell et al. (2002), our first-step regression employs establishment fixed effects. However, it is not possible to split off the establishment’s fixed effect as given in Equation (10). Therefore, in the first step, we estimate a “summary fixed effect” μn as observed from Equations (8) and (9), which is the response variable in the second-step regression.
The μn contain not just the “pure” establishment fixed effect θn but also all other time invariant variables and fixed effects from other levels of the hierarchy. Determinants working at different levels of the hierarchy are separated in the second-step regression. The predicted μn in Models 1 and 2 do not vary over time. Therefore, the second step includes one observation per establishment. The explanatory industry and regional variables relate to the time average of the overall sample period, when the establishment was observed. They are therefore indicated by a bar in (10).
To identify the consistent parameters of γ in the first-step regression, we also need to determine that the time-variant error ϵnt is uncorrelated with the establishment variables, which are included in the regression. Such a correlation appears when reverse causality is expected; this is especially the case for wages paid to an establishment’s workers. Establishments that are more productive can afford to pay higher wages. We therefore instrument wages and use wages paid by the establishment in the previous year as an internal instrument. Additionally, the average regional wage of the last year is included as an external instrument. This inclusion is because many German establishments are part of tariff unions.
In Models 1 and 2, the prediction for the second-step regression is corrected for the productivity effects of the establishment under consideration. The second-step regression is based on the following equation (Greene 2011):
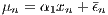 | (11) |
However, there are several additions to make: The μn are establishment-specific, but all establishments located in region r reveal the productivity (dis-)advantage of r and i as presented in (10); that is, if there are any. In other words, if there is a region that is relatively more productive than another, all individual productivity parameters μn will be relatively larger compared to the less productive region. A similar argumentation holds for different industries. Thus, using all μn within a region and industry provides an estimate of r and i, the average labor productivity effect of the region and industry, respectively. Thus, a regional effect r and industry effect i can be integrated into the second-step regression (see Equation (12)).
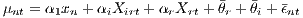 | (12) |
Equation (12) includes establishment-specific variables, which are time constant or are nearly time constant (xn), regardless of whether they are also included in (8) or (9); this is suggested by Greene (2011). In (8) or (9), a nearly time constant variable’s coefficient indicates the effect due to a change in time. Equation (12), however, estimates the effect of a level on the same variable, as opposed to the effect of a change. These effects on productivity of the within- and between-variation of variables can differ.
Equation (12) is written with a time index, which might be regarded as unexpected. The rationale is that the establishment panel is an unbalanced panel. On average, establishments are observed approximately 3.7 times. Therefore, the observations of single establishments cover different timespans; some are older and some are newer. The time-varying variables Xirt and Xrt are then averaged for the time span to which the observations of a single establishment are related. The variation in the establishment-specific time averages of the localization and urbanization measures then identifies the potential agglomeration effects.
In the second-step regression, we estimate the variants of Equations (11) and (12) by means of OLS while including different sets of explanatory variables and fixed effects. The outlined estimation strategy is therefore a strict approach to analyzing region-specific and industry-specific effects, which relate to agglomeration economies, as much variation is absorbed by fixed effects techniques and averaging.
4 Data
We aim to identify industry and region-time-specific labor productivity, θirt and θrt, which might be influenced by regional characteristics and the economic environment. The identification of these effects is based on the labor productivity of single establishments. This requires establishment- or firm-level data. We choose Germany as our research field because a rich database is available for this country, which suits our purpose. The IAB Establishment Panel (IAB-EP) is the only representative survey of establishments for a large economy that can be uniquely linked to other data sources. It is conducted on an annual basis and available for a relatively long time period. For the waves of 1995 to 2010, we use the vast information introduced in the following, which is especially relevant to our research program.
The IAB-EP surveys 16,000 establishments annually. To obtain a consistent data set, we only consider establishments that earn revenue and are sole traders, partnership companies, or corporate enterprises. This restriction excludes the public sector and, to some extent, financial institutions. We exclude 671 establishments that change either the reported industry or location based on NUTS3 regions. The exclusion of relocating firms addresses the emerging “selection effect” of firms that will overestimate agglomeration effects as indicated by Baldwin, Okubo (2006). After these preparatory steps, we can use approximately 8-9,000 establishments per wave. In total, we consider more than 27,000 establishments during the observation period.
The second data source is the Employment Statistics of Germany, which includes the entire population of people with gainful employment and social insurance coverage in Germany. Only the self-employed, civil servants, and workers with very low incomes are excluded from these data. The Employment Statistics give continuous information on employment spells, earnings, and job and personal characteristics. The statistics are based on microdata delivered by firms regarding their individual employees. For every employee, a new record is generated each year. If he or she changes work establishment, a new record is likewise generated. One of the advantages of the Employment Statistics is that it identifies the region where a specific employee is located.
Initially, the Employment Statistics data are collected for administrative purposes of the social security system, and are then collected by the administration of the Federal Employment Services. Because the data are used to calculate the pensions of retired people, the income and duration information is reliable. No wage classifications are needed because the Employment Statistics report exact individual wages. The wage variable measurement is in calendar days. Our institute, the IAB, has prepared and cleaned the statistics in a way that makes them useful for scientific analyses. This version of the database is called IAB Employment Statistics (IAB-ES). Apart from the individual wage, which is averaged at the establishment level, additional variables are used in our regressions.
In the context of our analyses, the use of the IAB-ES is twofold: On one hand, an employer-employee database is constructed by adding the information from the Employment Statistics to the individual establishment it is related to. This is relevant in the case of the human capital variable because of adding the share of highly qualified in the respective establishments. On the other hand, the information from the Employment Statistics was aggregated for further characterization of the industries and regions under observation, and this information was used to identify agglomeration effects.
Our response variable comes from the IAB-EP. It is the level of turnover or revenue, which is received by the respective establishments in the market, divided by the number of workers. Because it also relates to the stock of capital and the intermediate products used, it is an adequate measure of productivity (see section 2.1).
From the IAB-EP, we gather more information concerning additional control variables. Because Melitz (2003) argues exporting firms have to be more productive than non-exporting firms to compete in foreign markets are, we use the export proportion of total sales as a proxy for international competitiveness. Thus, such trade-related productivity effects are already absorbed from the remaining labor productivity parameter. We also use a dummy indicator that is set to unity if the establishment is foreign owned. Foreign owners may have an interest in higher dividends and, thus, more productive companies. The empirical evidence for Spain offered by Benfratello, Sembenelli (2006), however, suggests that foreign ownership does not influence productivity.
We employ two dummy indicators for the legal status, i.e., whether the firm is a sole trader or a private partnership. The reference category comprises all types of capital companies (for instance, stock corporations and other legal forms). As a proxy for the productivity of capital, we use information on the state of the type of technology and machinery. This ordinal set includes “newest”, “new”, “old,” and “out of date” to categorize equipment. The reference category is “newest technology”. As an additional control variable, we employ two dummy indicators for the establishment age. The first is set to unity if the life of the establishment is more than 4 years and less than 15 years; the second refers to an establishment with an age equal to or higher than 15 years. The reference category is therefore an age of up to 4 years.
Insourcing and outsourcing or spin-offs of companies would directly lead to a change in labor demand, as parts of the economic activities now take place within or outside of the establishment. Therefore, it is worthwhile to control for them: Two indicators are set to unity if parts of the establishment were insourced and outsourced. Employment Statistics data come from a consolidated file called the IAB Employment History File (IAB-EH), which is combined with the establishment panel on an annual basis. It contains not only information on the workforce employed on a reference day, but also the workforce employed throughout the year. It therefore takes seasonal employment differences explicitly into account. The IAB-EH provides detailed information on the occupations of the workforce represented by 2-digit occupational classifications (KldB 88). We use this information and compute diversity indices based on the fractionalization index for employees in less complex (low-skilled) and complex (high-skilled) occupations (see below).
Because the theoretical approach suggests controlling for intermediates, we make use of the IAB-EP survey data, which provides the proportion of intermediates in production. They are included as a regressor.
We refrain from using standard measures of human capital, such as the attainment of university degrees, for three reasons. First, there is a trend in the data indicating that the number of missing values of the educational attainment increases, whereas the proportion of people holding a university degree decreases over time. Second, Brunow, Hirte (2009) indicate that a measure built on educational attainment is biased, as it does not account for “over” or “undereducation.” This argument comes from a strand of literature started by Duncan, Hoffmann (1981). Third, Autor et al. (2003) establish a task-based approach for jobs, which relates to the amount of routine tasks and analytical tasks in the workplace. The advantage of the task-based approach is that it overcomes the problem of measuring mismatches such as overeducation because occupations are classified on both formal qualifications and the tasks performed.
Our classification of human capital is inspired by Gathmann, Schönberg (2010). We use the German Qualification and Career Survey, which was jointly conducted by the Federal Institute for Vocational Education and Training (BIBB) and the Institute for Employment Research (IAB) for 1998/1999. From this survey, we relate occupations to tasks and cluster occupations (see Spitz-Öner 2006, based on Autor et al. 2003) based on the average time spent with analytical work relative to analytical and manual work. Second, we calculate the share of non-routine work relative to routine and non-routine work. Finally, we use the proportion of human capital in the occupation based on formal qualification. According to our definition, which has previously been used by Trax et al. (2012) and Brunow, Nafts (2013), a complex occupation exhibits a relatively high proportion of time spent in non-routine and analytical work, and typically, the proportion of highly qualified people is relatively large. Following this, other occupations are then sorted into the “less complex” occupations group. For the sake of labeling, we henceforth use the term “low-skilled” and “high-skilled” for “less complex” and “complex” occupations, respectively. The classification is based on a hierarchical cluster analysis using the average linkage method.
Because the IAB-EH covers the entire population of all employees subject to social security, we are able to construct additional measures from this data source that are related not to individual establishments, but to industrial and regional units. First, we compute the total number of establishments that operate in the same 2-digit industry and that are located in the region. Second, we aggregate individual data within the regional workforce employed and use the proportion of people working in high-skilled occupations, again measured in full-time equivalents within the industry, to which the establishment is assigned.
For some of the variables, we also use a spatially lagged version. These lagged variables are calculated by multiplication with a row-standardized, spatial weights matrix. An element wij of this matrix W is computed by wij = exp(-ϕdij), where dij relates to the distance of the geographical centers of two regions i and j, and ϕ is a distance-decay parameter. The parameter is set such that from the average neighboring region (which has an average distance of 34 km), 70% of the effect is present. Experiments with a variation of this parameter exhibit only very small differences in the regression results.
As per Combes et al. (2004)’s suggestion, we use measures to control for the industrial variety diversity in a region. The number of regional established 2-digit industries aims to control for the variety of products and services available to the establishment. We also compute a diversity measure based on the fractionalization index, which captures the relative distribution of establishments across the industries. This measure increases the more uniform the distribution of establishments across industries is. Both measures relate to urbanization externalities.
We use the population density of districts in Germany, obtained from the German official statistics. This is one of the most important variables for indicating the presence of agglomerations in the country. The expectation is that the cost of population concentration, which is directly affected by high land prices (and high rents for flats and also relatively high regional prices; see Blien et al. 2009) and indirectly by the cost of congestion and of pollution, must be offset by the relatively high productivity of the establishments located there. Regional population is also a measure of market size (see, e.g., the theoretical contribution of Baldwin 1999).
Our regional units are the previously mentioned districts (i.e., in German terms “Landkreise” and “kreisfreie Städte”), which are relatively small, as there are 412 in the country; 411 of these regional units are represented in our sample. The size of the units provides a detailed picture. The disadvantage of the small-scale regional grid is compensated for by the use of the previously mentioned weight matrices, which describe the interdependencies of regions. Our establishment survey is sufficiently representative of the regions
Additionally, we use a typology of districts, which is generated by the application of two criteria: Centrality at the level of larger regions and population density at the level of districts. This typology has been developed and regularly updated by the German institute, BBSR (see Görmar, Irmen 1991, and later versions from the homepage of BBSR). Table 4 shows definitions of this typology. Table A.1 of the Appendix shows an overview and brief description of the variables used in the empirical study for establishment characteristics, and Table A.2 for industry and regional variables.
5 Results
Table 1 contains the first-step regressions of Model 1. The first column contains the result of a standard fixed effects (FE) model. All time constant variables disappear due to the fixed effects (within) transformation. In the second column, wages are instrumented (FE-IV). The tests show that the IV model does not suffer from weak instruments. The Hansen J-test indicates that the instruments are valid. Reported standard errors are robust to the presence of arbitrary heteroskedasticity. Model 2 is also estimated, but is not reported, because the results differ only slightly from those of Model 1.
| Response variable: Sales per worker | (1) FE | (2) FE-IV |
| log wages nt | 0.355*** | 0.619*** |
| (0.037) | (0.048) | |
| Prop. Exports | 0.193*** | 0.174*** |
| (0.033) | (0.028) | |
| Prop. high skilled | 0.146** | 0.045 |
| (0.060) | (0.048) | |
| Prop. Intermediates | 0.100*** | 0.096*** |
| (0.013) | (0.012) | |
| Frac. occupation, low-skilled | -0.697*** | -0.655*** |
| (0.035) | (0.028) | |
| Frac. occupation, high-skilled | -0.356*** | -0.301*** |
| (0.033) | (0.024) | |
| Prop. high-skilled foreigners | -0.041 | -0.031 |
| (0.054) | (0.044) | |
| Frac. high-skilled foreigners | 0.072 | 0.078 |
| (0.070) | (0.057) | |
| log No. high-skilled nationalities | -0.113*** | -0.112*** |
| (0.040) | (0.032) | |
| Outsourcing | 0.033*** | 0.037*** |
| (0.011) | (0.011) | |
| Insourcing | -0.006 | -0.000 |
| (0.011) | (0.011) | |
| D foreign owner | 0.034 | 0.030 |
| (0.024) | (0.018) | |
| D partnership company | -0.049*** | -0.035*** |
| (0.017) | (0.012) | |
| D sole trader | -0.036* | -0.020 |
| (0.020) | (0.015) | |
| D new equipment | -0.007 | -0.008 |
| (0.006) | (0.005) | |
| D old equipment | -0.019** | -0.017*** |
| (0.008) | (0.007) | |
| D out-of-date equipment | -0.040*** | -0.033** |
| (0.014) | (0.013) | |
| D establ. age 5-14 years | 0.000 | 0.005 |
| (0.013) | (0.011) | |
| D establ. age 15 years and more | -0.014 | -0.012 |
| (0.014) | (0.012) | |
| Time FE | Yes | Yes |
| Establishment FE | Yes | Yes |
| N / No. of establishments | 98,067 / 27,887 | 82,390 / 25,500 |
| Within R2 | 0.087 | |
| Hansens J | 0.160 | |
| Kleibergen-Paap rk LM statistic | 709.715*** | |
| F-Test | 49.996*** | 85.056*** |
Note: Establishment FE included; robust s.e. in (); * p <0.1; ** p <0.05; *** p <0.01;
Frac.: Fractionalization index; D: Dummy; Prop.: Proportion; establ.: establishment; col: collinear with
establishment FE
In Table 1, the estimated coefficients reveal the expected signs. The coefficient of wages is 0.351 in the FE regression and 0.635 in the FE-IV estimation. The results suggest that labor and capital are complements rather than substitutes because the estimate is less than 1. Considering the employment structure, we find a significant and positive effect of employing high-skilled workers. The effect becomes insignificant after instrumenting wages. This is not surprising, as wages already capture human capital effects: If there are relatively more highly-skilled employees, wages should be higher. As wages are also instrumented with lagged values, the skill information is partly included in the instrument. Thus, the estimate of the wage rate increases to 0.6. This result is one of the key findings of the work conducted by Mankiw et al. (1992).
Melitz (2003) argues that exporting firms have to be relatively more productive to be able to compete in foreign markets. If the proportion of exports to revenues increases, labor productivity is higher. As the results in Table 1 show, Melitz’s argument on productivity and trade is supported. If the equipment and machinery employed in the production process ages, the establishment’s productivity decreases. This may reflect the progress of the product life cycle, but also the productivity disadvantages of old equipment. In regards to the product life cycle, and therefore to the establishment age, we do not find any significant effect of aging. If the establishment matures, it does not become more or less productive.
In focusing on occupational diversity among employment groups, we provide evidence that a diverse set of employees is accompanied by productivity losses. This initially does not seem to be clear. However, if the fragmentation of occupations is too strong, it is likely that the establishment does not focus on a specific task/production process and is therefore disadvantaged with respect to labor productivity. As expected, this disadvantageous effect is smaller for highly-skilled occupations.
Considering the cultural diversity of high-skilled employees, we support the earlier findings of Brunow, Blien (2014), which focus on overall diversity. However, according to Brunow, Nijkamp (2012), productivity differences due to the cultural diversity of low-skilled people do not occur, and correspondingly, we only find evidence of such differences for the high-skilled group. The proportion of employed foreigners is insignificant. Thus, on average, there is no general negative effect of employing foreigners. However, an increase in the figure of nationalities employed has negative effects.
It is important to control other variables to properly assess the presence and size of agglomeration effects. These variables, however, are time constant or nearly time constant. Therefore, these variables are included in the second step of the regression. The two models of Table 1 do not differ in terms of interpretation; however, because the IV model adjusts for wage endogeneity, it is preferred. From this regression, we compute the establishment fixed effect μn, which becomes the response variable in the regression of step two.
In the second-step regressions, each observation represents the fixed effect received in the first-step regression. Therefore, the precision of the estimation of the establishment fixed effects depends on the number of observations available in the first-step regression. To account for the preciseness in the second step, each observation is weighted with the number of observations used to identify the establishment fixed effects in the first step.
Tables 2, 3, and 4 present the results of several variants of the second step regressions. The explanatory variables are computed by the time average of each variable when the individual establishment is observed. Depending on the specification, there are approximately 25,000 distinct establishments surveyed over time. In all empirical models, industry fixed effects are included, as the theoretical model suggests. Reported standard errors are clustered at the regional level to account for the likely correlation among establishments within the region.
The first column of Table 2 is a baseline specification, which includes some of the crucial variables indicating agglomeration and controls for (nearly) time constant establishment characteristics. The latter group of variables comprises dummies indicating various forms of ownership, modernity of equipment, establishment age, outsourcing, and insourcing. These variables are included in all models of the following tables to control for the heterogeneity of the population. They are not noteworthy in the present context, and their coefficients are therefore omitted. They are largely in line with expectations and are presented in Table A.3 in the Appendix.
In Column (2), regional fixed effects are added. In the following columns, different variables are added to check for various aspects of agglomeration. Some of the exogenous variables are also included with a spatial lag: They are multiplied by a spatial weight matrix W. The models of Columns (9) and (10) consider nine different district types by means of dummy variables instead of region fixed effects. Parameters do not vary greatly between the two specifications.
We now ask whether the establishment effects are influenced by agglomeration forces while controlling for a variety of fixed effects and establishment characteristics. The inclusion of the latter variables allows for proper identification of the agglomeration effects. This increases the difficulty for agglomeration variables to become significant, as they are no longer biased upward. Therefore, we perform a strong test of agglomeration forces. With some variables, this test is not possible because they vary only minimally between time periods.
Examining the agglomeration variables shows that a larger number of industries within the region does not matter. This may be because the variation in the number of industries measured at the 2-digit level between regions is relatively small. The fractionalization of industries within a region matters, however: In regions where the number of operating establishments has an equal distribution over industries, labor productivity is higher on average. Both measures are related to a special form of urbanization externality, namely, the Jacobs effect (Jacobs 1969). It is important that the diversity of the industrial composition matters for productivity. We also tested the interaction effects of both variables, which, however, were insignificant.
| Response variable: FE of step 1 | (1) | (2) | (3) | (4) | (5) | (6) |
| log No. industries | 0.099 | 0.132 | -0.046 | 0.093 | 0.084 | 0.119 |
| (0.194) | (0.418) | (0.222) | (0.418) | (0.164) | (0.421) | |
| Frac. of establ. over industries | 3.877*** | 10.971*** | 6.357*** | 11.539*** | 3.929*** | 10.771*** |
| (1.219) | (3.713) | (1.061) | (3.902) | (1.237) | (3.695) | |
| log prop. high-skilled empl. | 0.377*** | 0.353*** | 0.422*** | 0.352*** | 0.359*** | 0.338*** |
| within ind. rt | (0.083) | (0.079) | (0.086) | (0.079) | (0.082) | (0.079) |
| W log prop. high-sk. empl. | 0.170 | 0.429 | 0.125 | 0.433 | 0.078 | 0.288 |
| within ind. -rt | (0.309) | (0.314) | (0.307) | (0.314) | (0.305) | (0.316) |
| log No. establ. | 0.016 | 0.034* | 0.021 | 0.034* | ||
| within industry rt | (0.012) | (0.017) | (0.018) | (0.017) | ||
| W log No. establ. | -0.059 | -0.039 | -0.044 | -0.039 | ||
| within ind. -rt | (0.041) | (0.054) | (0.053) | (0.053) | ||
| log employment | 0.014** | 0.019*** | ||||
| within industry rt | (0.007) | (0.007) | ||||
| W log employment | 0.002 | 0.017 | ||||
| within industry -rt | (0.019) | (0.019) | ||||
| log population density rt | 0.006 | -0.120 | 0.006 | -0.135 | ||
| (0.007) | (0.218) | (0.007) | (0.220) | |||
| W log population density -rt | 0.171*** | 0.779* | 0.154*** | 0.674 | ||
| (0.028) | (0.438) | (0.026) | (0.442) | |||
| log population rt | -0.002 | -0.022 | ||||
| (0.022) | (0.262) | |||||
| W log population -rt | 0.217*** | 0.796 | ||||
| (0.076) | (0.556) | |||||
| Time constant establ. characteristics | yes | yes | yes | yes | yes | yes |
| Industry FE | yes | yes | yes | yes | yes | yes |
| Region FE | no | NUTS3 | no | NUTS3 | no | NUTS3 |
| N | 25,5 | 25,5 | 25,5 | 25,5 | 25,5 | 25,5 |
| R2 | 0.302 | 0.324 | 0.300 | 0.324 | 0.302 | 0.324 |
Region-cluster robust standard errors. in (); * p <0.1; ** p <0.05; *** p <0.01;
Frac.: Fractionalization index; establ.: establishment; Prop.: Proportion; W: row-standardized spatial
weights matrix; Region FE relates to NUTS3-region fixed effects.
A subset of the included variables is related to the Marshall-Arrow-Romer (MAR) agglomeration forces within an industry. The number of establishments located in the region (and its spatial lag) is a measure of the bulk of production taking place in these locations. The variable also indicates production chains of horizontal and vertical linkages within the two-digit industries. Finally, it serves as a measure of competition intensity. It is insignificant in the basic regression without regional fixed effects but becomes weakly significant in the FE model. If more establishments of a specific industry are located within the region, average labor productivity increases. Thus, supply chains and stronger competition within a regional industry relate (weakly) to labor productivity gains.
| Response variable: FE of step 1 | (7) | (8) | (9) | (10) |
| log No. industries | -0.033 | 0.080 | -0.023 | -0.105 |
| (0.223) | (0.421) | (0.206) | (0.182) | |
| Frac. of establ. over industries | 6.269*** | 11.303*** | 6.845*** | 6.940*** |
| (1.068) | (3.892) | (1.199) | (1.188) | |
| log prop. high-skilled empl. within ind. rt | 0.396*** | 0.338*** | 0.367*** | 0.351*** |
| (0.085) | (0.079) | (0.084) | (0.084) | |
| W log prop. high-sk. empl. within ind. -rt | 0.031 | 0.292 | 0.176 | 0.021 |
| (0.308) | (0.316) | (0.311) | (0.310) | |
| log No. establ. within industry rt | -0.000 | |||
| (0.011) | ||||
| W log No. establ. within ind. -rt | 0.050 | |||
| (0.039) | ||||
| log employment within industry rt | 0.017** | 0.019*** | 0.008 | |
| (0.007) | (0.007) | (0.007) | ||
| W log employment within industry -rt | 0.004 | 0.017 | 0.036* | |
| (0.020) | (0.019) | (0.019) | ||
| log population density rt | Col with DTYP
| |||
| W log population density -rt | Col with DTYP
| |||
| log population rt | 0.000 | -0.039 | Col with DTYP
| |
| (0.015) | (0.264) | |||
| W log population -rt | 0.170*** | 0.678 | Col with DTYP
| |
| (0.062) | (0.564) | |||
| Time constant establ. characteristics | yes | yes | yes | yes |
| Industry FE | yes | yes | yes | yes |
| Region FE | no | NUTS3 | DTYP | DTYP |
| N | 25,5 | 25,5 | 25,5 | 25,5 |
| R2 | 0.300 | 0.324 | 0.300 | 0.301 |
Region-cluster robust standard errors. in (); * p <0.1; ** p <0.05; *** p <0.01;
Frac.: Fractionalization index; establ.: establishment; Prop.: Proportion; W: row standardized spatial
weights matrix; Region FE relate to either NUTS3-region fixed effects or 9 district types (DTYP)
provided by BBSR.
As a further variable, we include the intra-industrial proportion of highly skilled workers, excluding the contribution of the establishment under consideration. This variable serves as a proxy for intra-industrial knowledge spillovers and knowledge intensity. This variable is significant and positive in all models. Establishments located in an environment of knowledge-intense competitors within an industry are on average more productive. This is an important result, which can also be related to endogenous growth theory, which suggests knowledge spillovers between firms are a key driver of growth.
Measures of urbanization are the size of the population itself and the population density in the respective area. In the new economic geography literature, population size serves as a measure of demand because the level of regional expenditures is linked to the regional population (Krugman 1991). A frequent argument is that being closer to larger markets enhances demand, which is associated with increasing returns and thus with higher productivity (Brunow, Nijkamp 2012). The estimates on population density support this argument (Columns (1), (2), (5), and (6)). In the fixed effects models, the between-region variation is lost, and therefore, it is not surprising that the effect becomes insignificant because the population density is nearly time constant. As an alternative, we employ the size of the regional population (Columns (3), (4), (7), and (8)) instead of population density and find a positive effect of the spatially lagged variable. The direct effect of population and of population density is not significant in any of the models discussed because of the multicollinearity with other variables, especially with the proportion of high-skilled employees.
As an alternative measure of urbanization, we use the employment levels and their spatial lag (Columns (5) to (8) and (10)), excluding the employment level of the establishment under consideration. In this case, the direct effect is nearly always significant. This is a strong result for the relevance of agglomeration effects. A larger workforce employed in a specific industry is associated with labor productivity gains. Arguably, this effect is due to common labor markets and spillover effects. The spatial lag of this variable is not significant in most models.
The number of establishments within a region and an industry (Columns (1) to (4), and (9)) is a variable that shows similar results to those of the employment level. Both variables – the number of establishments and the employment levels – and their spatial lags, which are not significant, relate to MAR externalities. We also include both variables in a regression, but the picture does not change greatly, although both variables are collinear, and the spatial variables become highly significant with the opposite sign as the corresponding non-spatial variables have. Therefore, they should be regarded separately.
Table 4 presents results using a widespread and simple classification system for German regions developed by the BBSR, a spatial research institute. Districts are classified according to the criteria of density and centrality. Both are important to describe an agglomeration. Because the districts are the regional units we use in this paper, the regional fixed effects cannot be included. Additionally, the classification uses population density; therefore, this variable is excluded from the regression model. The classification system takes control of regional effects in ‘similar’ regions but is less restrictive than the pure region fixed effects model.
The coefficients of the other variables are presented in Table 3, Column (9) and (10), and the results for the district types are presented in Table 4. They indicate significant differences between regional types. The main result is that centrality matters for productivity differentials. The most productive regions are those in the center of a metropolitan area.
| Parameter estimates
| |||||
| Level of | Column (9) | Column (10)
| |||
| larger | Table 2b | Table 2b
| |||
| regions | District level | b | s.e. | b | s.e. |
| Regions with large agglomerations
| |||||
| 1. Core cities | 0.084** | (0.036) | 0.075** | (0.035) | |
| 2. Densely populated areas | 0.082** | (0.033) | 0.078** | (0.033) | |
| 3. Populated areas | 0.034 | (0.038) | 0.033 | (0.038) | |
| 4. Rural areas | -0.016 | (0.034) | -0.014 | (0.034) | |
| Regions with conurbational features
| |||||
| 5. Core cities | 0.023 | (0.038) | 0.020 | (0.038) | |
| 6. Populated areas | -0.000 | (0.034) | -0.004 | (0.034) | |
| 7. Rural areas | -0.000 | (0.032) | -0.001 | (0.031) | |
| Rural regions
| |||||
| 8. Densely populated rural areas | 0.015 | (0.035) | 0.014 | (0.035) | |
| 9. Sparsely populated rural areas | Reference group | ||||
Parameter estimates for district types of models (9) & (10) in Table 3, Region-cluster robust standard
errors (s.e.) in (); * p <0.1; ** p <0.05; *** p <0.01
6 Conclusion
In this paper, we have carried out empirical analyses based on a theoretical model of firms. The empirical results show that agglomeration effects are present for individual establishments. Because both localization and urbanization forces are important, the metropolitan areas are the engines of labor productivity in Germany.
It should be noted that the results concern the productivity of establishments and cannot be easily transferred to other economic variables. This is because agglomeration forces affect different economic variables differently (Rosenthal, Strange 2004, Puga 2010). Agglomeration effects on productivity and employment might be similar, or they might be contradictory, as Cingano, Shivardi (2004) have shown. Due to the labor-saving effect of productivity gains, agglomeration effects on productivity might affect employment negatively. On the other hand, increases in productivity typically reduce prices, and this might increase employment (see Combes et al. 2004, Blien, Sanner 2014). This compensating effect on employment might be even stronger than the labor-saving effect. Thus, the productivity effect of agglomerations on employment is an empirical question. This can explain the different results on employment obtained in various empirical studies. Large parts of the empirical literature have concentrated on employment and wages, whereas we address productivity. We use a flexible and comprehensive operationalization of productivity, as it is measured by the empirical approximation of the production function derived from theory. Productivity in this sense is turnover per worker related to the complete use of labor, capital, and intermediate products.
The analysis concerns one of the critical questions of regional economics. Agglomeration effects are expected to occur due to the “Marshallian forces”: Common labor markets, knowledge spillovers, and forward and backward linkages between firms or establishments foster higher productivity in areas more densely populated by firms and people. Although there has been much research on the existence of these forces, many of the empirical studies were affected by limitations concerning the units of observations. Many of the studies operate at an aggregate level, which does not allow for a precise measurement of agglomeration forces. In this study data, we use individual establishments to assess the effects expected from theoretical considerations. Aggregation could mask the important relationships and could produce an “ecological fallacy” by erroneously transferring a connection between variables found at the aggregate level to the micro-level.
The empirical part of this paper shows in detail that agglomeration effects are present in Germany. Localization, especially intra-industrial human capital spillovers and urbanization forces measured by the local economic industrial diversity, are both important. The metropolitan areas are those regions that are the engines of productivity in the country. Regions have differential consequences for the establishments in their territories. Densely populated metropolitan areas are those in which the establishments reach the highest levels of labor productivity, whereas rural regions outside agglomerations are disadvantaged. The analysis for district types indicates that this conclusion is justified even within a metropolitan area. Establishments located near the core of an agglomeration are not as productive as are those that are precisely within the core. Our approach uses relatively small regional units, which facilitates the identification of these differences.
The conclusion concerning agglomeration forces can be drawn even after controlling for important individual-level variables. The respective industry and the modernity of the production equipment clearly influence the productivity of a firm. However, the effect of the concentration of economic activity remains after controlling for these variables. Therefore, this approach makes it possible to closer observe the forces that have an influence on the interaction between regions and establishments. The conclusion is that the location of an establishment influences its productivity. In addition to various forms of concentration that can be demonstrated to have an effect, the diversity of a region is also important. Therefore, not only are Marshall-Arrow-Romer effects present, especially the knowledge spillover, but also Jacobs effects.
References
Autor D, Levy F, Murnane R (2003) The skill content of recent technological change: An empirical exploration. The Quarterly Journal of Economics 118: 1279–1333
Baldwin J, Brown M, Rigby D (2010) Agglomeration economies: Microdata panel estimates from canadian manufacturing. Journal of Regional Science 50: 915–934
Baldwin R (1999) Agglomeration and endogenous capital. European Economic Review 43: 263–280
Baldwin R, Okubo T (2006) Heterogeneous firms, agglomeration and economic geography: spatial selection and sorting. Journal of Economic Geography 6: 323–346
Bell B, Nickell S, Quintini G (2002) Wage equations, wage curves and all that. Labour Economics 9: 341–360
Benfratello L, Sembenelli A (2006) Foreign ownership and productivity: Is the direction of causality so obvious? International Journal of Industrial Organization 24: 733–751
Blien U, Gartner H, Stüber H, Wolf K (2009) Regional price levels and the agglomeration wage differential in Western Germany. The Annals of Regional Science 43: 71–88
Blien U, Sanner H (2014) Technological progress and employment. Economics Bulletin 34: 245–251
Brunow S, Blien U (2014) Effects of cultural diversity on individual establishments. International Journal of Manpower 35: 166–186
Brunow S, Hirte G (2009) Regional age pattern of human capital and regional productivity: A spatial econometric study on German regions. Papers in Regional Science 88: 799–823
Brunow S, Nafts V (2013) What types of firms tend to be more innovative: a study on Germany. Norface migration discussion paper 2013/21, Norface Research Programme on Migration, London
Brunow S, Nijkamp P (2012) The impact of a culturally diverse workforce on firms’ market size: an empirical investigation on germany. Norface migration discussion paper 2012/22, Norface Research Programme on Migration, London
Card D (1995) The wage curve: A review. Journal of Economic Literature 33: 785–799
Cingano F, Shivardi F (2004) Identifying the sources of local productivity growth. Journal of the European Economic Association 2: 720–742
Combes P, Gobillon L (2014) The empirics of agglomeration economics. In: Duranton G, Henderson V, Strange W (eds), Handbook of Regional and Urban Economics. Elsevier, Amsterdam
Combes P, Magnac T, Robin J (2004) The dynamics of local employment in France. Journal of Urban Economics 56: 217–243
Drucker J, Feser E (2012) Regional industrial structure and agglomeration economies: An analysis of productivity in three manufacturing industries. Regional Science and Urban Economics 42: 1–14
Duncan J, Hoffmann S (1981) Overeducation, undereducation, and the theory of career mobility. Applied Economics 36: 803–816
Duque J, Artís M, Ramos R (2006) The ecological fallacy in a time series context: Evidence from Spanish regional unemployment rates. Journal of Geographical System 8: 391–410
Duranton G, Puga D (2004) Micro-Foundations of urban agglomeration economies. In: Henderson J, Thisse J (eds), Handbook of Regional and Urban Economics. Elsevier, Amsterdam
Gathmann C, Schönberg U (2010) How general is human capital? A task-based approach. Journal of Labor Economics 28: 1–49
Glaeser E, Ponzetto G, Tobio K (2011) Cities, skills, and regional change. NBER Working Paper 16934, National Bureau of Economic Research
Greene W (2011) Fixed effects vector decomposition: A magical solution to the problem of time-invariant variables in fixed effects models? Political Analysis 19: 135–146
Görmar W, Irmen E (1991) Nichtadministrative Gebietsgliederungen und -kategorien für die Regionalstatistik. die siedlungsstrukturelle Gebietstypisierung der BfLR. Raumforschung und Raumordnung 49: 387–394
Henderson J (2003) Marshall’s scale economies. Journal of Urban Economics 53: 1–28
Jacobs J (1969) The Economy of Cities. Random House, New York
Krugman P (1991) Increasing returns and economic geography. Journal of Political Economy 99: 483–499
Mankiw NG, Romer D, Weil DN (1992) A contribution to the empirics of economic growth. The Quarterly Journal of Economics 107: 407–437
Marshall A (1920) Principles of Economics. Macmillan, London
Melitz M (2003) The impact of trade on intra-industry reallocations and aggregate industry productivity. Econometrica 71: 1695–1725
Moretti E (2004) Education, spillovers and productivity. American Economic Review 94: 656–690
Plümper T, Troeger V (2007) Efficient estimation of time-invariant and rarely changing variables in finite sample panel analyses with unit fixed effects. Political Analysis 15: 124–139
Puga D (2010) The magnitude and causes of agglomeration economics. Journal of Regional Science 50: 203–219
Rosenthal S, Strange W (2004) Evidence on the nature and sources of agglomeration economies. In: Henderson J, Thisse J (eds), Handbook of Regional and Urban Economics. Elsevier, Amsterdam
Spitz-Öner A (2006) Technical change and job tasks, and rising educational demands: Looking outside the wage structure. Journal of Labor Economics 24: 235–270
Trax M, Brunow S, Suedekum J (2012) Cultural diversity and plant level productivity. IZA discussion paper 6845, Forschungsinstitut zur Zukunft der Arbeit GmbH, Bonn
A Appendix
Construction of the human-capital measure
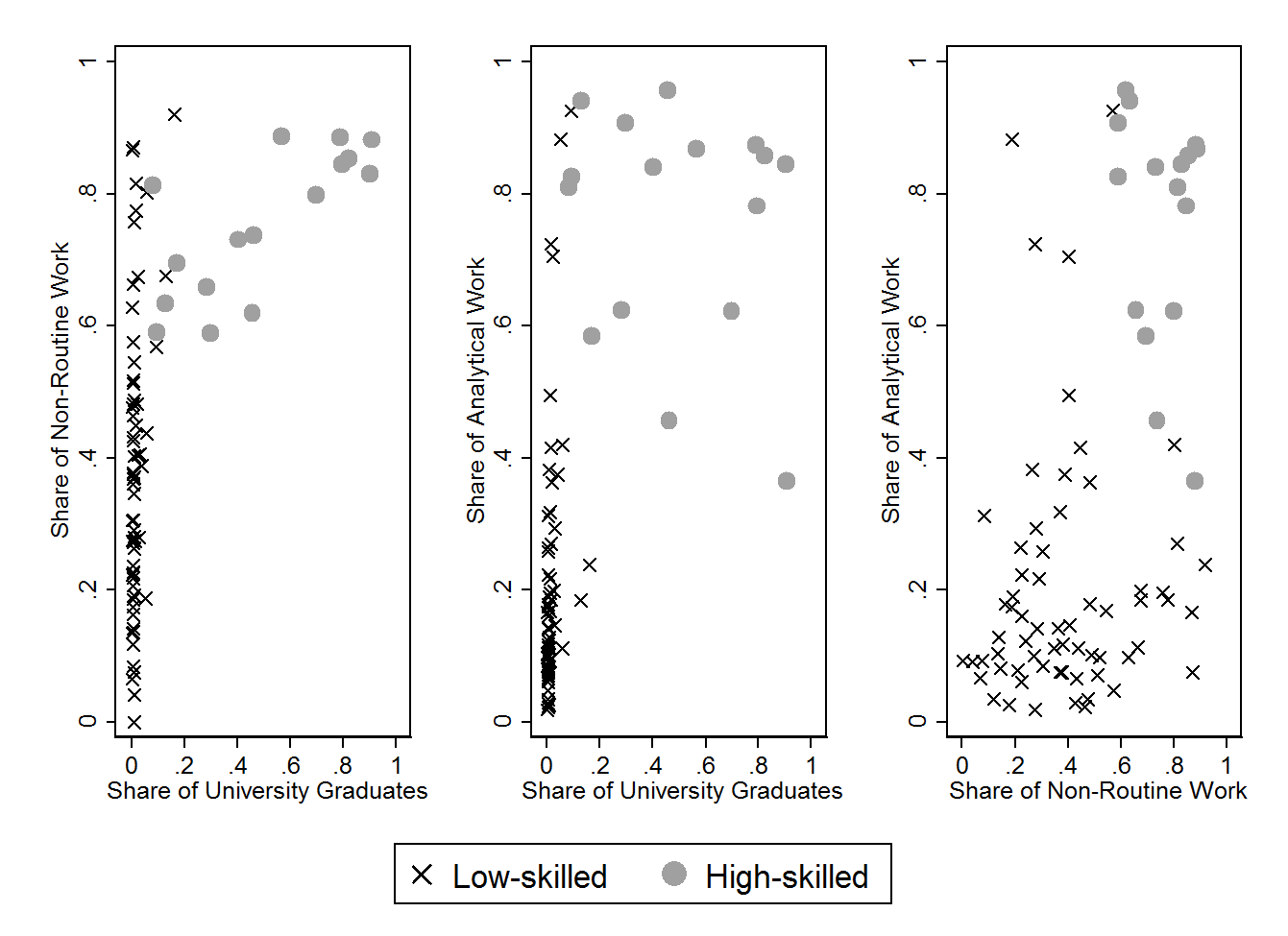
We make use of information on time spent in manual, analytical, routine and non-routine tasks and compute the proportion of time spent in analytical tasks relative to analytical and manual tasks and the proportion of time spent in non-routine relative to routine and non-routine tasks for 80 occupations based on the German occupational system KldB88. These data were collected from the German Qualification and Career Survey in 2006. Additionally, we construct the proportion of formal qualification using the IAB Employment Statistics for 2006. Formal qualification refers to university certificates. These three proxies describe the task content and the formal qualification requirement for each occupation. It is expected that occupations with a high degree of analytical and non-routine tasks and a relatively higher proportion of “highly skilled” people is associated with complex tasks and thus relates to a task-based approach of measuring human capital.
Using these three proportions, a cluster analysis was conducted. The (hierarchical) clustering method is the average linkage using Euclidean distance. Figure A.1 provides the results of the cluster analysis. Each dot indicates a single occupation that is identified as a highly skilled job; this cross-relates to the low-skilled occupations. As observed, highly skilled occupations are typically those with a higher proportion of university degree holders; the tasks in the job are rather non-routine and have a higher proportion of analytical work. Thus, it is in line with the intuition of the task-based approach.
The results of the cluster analysis of occupations are then used to compute the human capital-related measures. Because the special data preparation of the IAB-ES reports all information separated by occupations, a unique aggregation can be applied.
Variable descriptions and control variable results
| Data | Proxy for
| ||
| Variable | Description | Source | eq. (7)
|
| D foreign owner | Foreign ownership (yes/no) | IAB EP | θn |
| D partnership company | Partnership company (yes/no) | IAB EP | θn |
| D sole trader | Sole trade (yes/no) | IAB EP | θn |
| D establ. age 5-14 years | Establ. age between 5-14 years (Dummy) | IAB ES | θn |
| D establ. age 15+ years | Establ. age 15 years and more (Dummy) | IAB ES | θn |
| Outsourcing | Parts of the establ. were outsourced | IAB EP | θn,Xnt |
| (yes/no) | |||
| Insourcing | Parts of the establ. were insourced | IAB EP | θn,Xnt |
| (yes/no) | |||
| D new equipment | Establ. operates with new equipment | IAB EP | Znt |
| (Dummy, reference: newest equipment) | |||
| D old equipment | Establ. operates with rather old | IAB EP | Znt |
| equipment (Dummy, reference: | |||
| newest equipment) | |||
| D out-of-date equipment | Establ. operates with out-of-date | IAB EP | Znt |
| equipment (Dummy, reference: | |||
| newest equipment) | |||
| log wages nt | Logarithm of average daily wages | IAB ES | ln wnt |
| paid to employees | |||
| Prop. exports | Proportion of exports on revenues | IAB EP | θn |
| Prop. High-skilled | Proportion of high-skilled employees | IAB ES | Xnt |
| Frac. occupation, low-skilled; | Establishment diversity of employment | IAB ES | Xnt |
| Frac. occupation, high-skilled | over occupations employed within the | ||
| group of low-skilled (high-skilled) | |||
| employees; computed on the basis of | |||
| the fractionalization index | |||
| Prop. High-skilled foreigners | Proportion of high-skilled foreigners on all | IAB ES | Xnt |
| employed high-skilled workers | |||
| Frac. High-skilled foreigners | Diversity of high-skilled foreigners over | IAB ES | Xnt |
| nationalities; computed on the basis of | |||
| the fractionalization index | |||
| log No. high-skilled nationalities | Logarithm of the total number of foreign | IAB ES | Xnt |
| nationalities employed (zero for | |||
| establishments without high-skilled | |||
| foreign employees | |||
| Data | Proxy for
| ||
| Variable | Description | Source | of eq. (7)
|
| Industry related characteristics
| |||
| log No. establ. within industry rt | Logarithm of the number of | IAB EH | Xit |
| establishments within the industry | |||
| located in the same region | |||
| W log No. establ. within ind. -rt | Spatial lag of the number of | IAB EH | Xit |
| establishments within the industry | |||
| located in all other regions | |||
| log No. employees within ind. rt | Logarithm of the number of employees | IAB EH | Xit |
| within the industry located in the same | |||
| region; measured in full-time equivalents, | |||
| excluding the contribution of the | |||
| establishment under consideration | |||
| W log No. employees within | Spatial lag of the number of employees | IAB EH | Xit |
| ind. -rt | within the industry located in all other | ||
| regions; measured in full-time equivalents | |||
| log prop. high-skilled empl. | Logarithm of proportion of high-skilled | IAB EH | Xit |
| within ind. rt | employees within the industry located in | ||
| the same region; measured in full-time | |||
| equivalents, excluding the contribution of | |||
| the establishment under consideration | |||
| W log prop. high-sk. empl. | Spatial lag of proportion of high-skilled | IAB EH | Xit |
| within ind. -rt | employees within the industry located in | ||
| all other regions; measured in full-time | |||
| equivalents | |||
| Region related characteristics
| |||
| log No. industries | Logarithm of the number of industries | IAB EH | Xrt |
| (2-digit) within the region | |||
| Frac. of establ. over industries | Industrial diversity in the region measured | IAB EH | Xrt |
| as the distribution of establishments over | |||
| the industries (2-digit); computed on the | |||
| basis of the fractionalization Index | |||
| log population density rt | Logarithm of the regional population | Destatis | Xrt |
| density | |||
| W log population density -rt | Spatial lag of the population density of | Destatis | Xrt |
| all other regions (own computation) | |||
| Model: | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| Outsourcing | 0.359*** | 0.328*** | 0.363*** | 0.329*** | 0.353*** | 0.322*** | 0.358*** | 0.323*** | 0.361*** | 0.357*** |
| (0.069) | (0.071) | (0.068) | (0.071) | (0.069) | (0.071) | (0.068) | (0.070) | (0.068) | (0.068) | |
| Insourcing | 0.642*** | 0.616*** | 0.650*** | 0.617*** | 0.637*** | 0.613*** | 0.645*** | 0.614*** | 0.647*** | 0.643*** |
| (0.101) | (0.100) | (0.101) | (0.100) | (0.101) | (0.100) | (0.101) | (0.100) | (0.101) | (0.100) | |
| Foreign owner | 0.293*** | 0.278*** | 0.300*** | 0.278*** | 0.291*** | 0.275*** | 0.298*** | 0.275*** | 0.297*** | 0.295*** |
| (0.029) | (0.031) | (0.030) | (0.031) | (0.029) | (0.031) | (0.030) | (0.031) | (0.030) | (0.030) | |
| Private partnership | 0.075*** | 0.072*** | 0.073*** | 0.072*** | 0.074*** | 0.072*** | 0.074*** | 0.072*** | 0.074*** | 0.074*** |
| (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | |
| Sole trader | -0.113*** | -0.104*** | -0.115*** | -0.104*** | -0.112*** | -0.103*** | -0.113*** | -0.103*** | -0.113*** | -0.112*** |
| (0.014) | (0.015) | (0.015) | (0.015) | (0.015) | (0.015) | (0.015) | (0.015) | (0.014) | (0.015) | |
| New equipment | -0.092*** | -0.092*** | -0.093*** | -0.091*** | -0.092*** | -0.092*** | -0.093*** | -0.092*** | -0.094*** | -0.094*** |
| (0.019) | (0.019) | (0.018) | (0.019) | (0.019) | (0.019) | (0.018) | (0.019) | (0.018) | (0.018) | |
| Old equipment | -0.235*** | -0.243*** | -0.236*** | -0.243*** | -0.235*** | -0.243*** | -0.235*** | -0.243*** | -0.238*** | -0.237*** |
| (0.018) | (0.018) | (0.019) | (0.018) | (0.019) | (0.019) | (0.019) | (0.019) | (0.019) | (0.019) | |
| Out-of-date equipment | -0.351*** | -0.354*** | -0.347*** | -0.354*** | -0.349*** | -0.354*** | -0.346*** | -0.354*** | -0.353*** | -0.352*** |
| (0.031) | (0.031) | (0.031) | (0.031) | (0.031) | (0.031) | (0.031) | (0.031) | (0.031) | (0.031) | |
| Age 5-14 years | 0.067*** | 0.099*** | 0.053** | 0.099*** | 0.067*** | 0.100*** | 0.054** | 0.100*** | 0.061*** | 0.061*** |
| (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | (0.021) | |
| Age 15 years and older | 0.131*** | 0.119*** | 0.133*** | 0.120*** | 0.130*** | 0.120*** | 0.133*** | 0.120*** | 0.134*** | 0.133*** |
| (0.016) | (0.016) | (0.016) | (0.016) | (0.016) | (0.016) | (0.016) | (0.016) | (0.016) | (0.016) | |
Region-cluster robust standard errors. in (); * p <0.1; ** p <0.05; *** p <0.01