Volume
5, Number 3, 2018, 1–19 journal homepage:
region.ersa.org
Volume
5, Number 3, 2018, 1–19 journal homepage:
region.ersa.orgDOI: 10.18335/region.v5i1.195
Effectiveness of EU Regional Policy: Evidence from a Natural Experiment in Finland
1 National Audit Office of Finland, Helsinki, Finland Received: 29 May 2017/Accepted: 29 December 2017Abstract. European Union regional policy is implemented through structural funds, such as the European Regional Development Fund (ERDF), which supports investment in peripheral regions of the EU. We studied the effects of EU regional policy on key economic variables using a rare natural experiment setting. In 2007, parts of regions that were previously covered by the ERDF programme for Western Finland were reallocated to the ERDF programme for Northern Finland, with higher support intensity per capita. This reallocation was caused by the newly adopted EU legislation regulating the classification of regional statistical areas. With a detailed postal code area dataset and a difference-in-differences estimator, we discovered desirable regional policy effects on unemployment and the number of jobs.
Key words: Regional policy, Policy analysis, Microeconometrics
1 Introduction
The long-term growth programme of the European Union (EU), the Europe 2020 Strategy, was adopted in 2010. Following the Lisbon Strategy of the previous decade, the Europe 2020 Strategy aims to: (1) enhance employment; (2) increase research and development; (3) reduce greenhouse gas emissions; (4) improve tertiary education levels; and (5) reduce poverty in Europe. Precise target levels have been set for these objectives, both at the overall EU level and for each Member State. For instance, the employment rate target for the population aged 20-64 is 75%. According to Eurostat, the current (2016) figure for the 28 Member States of the European Union (EU28) is 71.1%1 .
One of the main instruments for achieving these targets is the EU’s regional policy. As stated by the European Commission, “EU regional policy is an investment policy. It supports job creation, competitiveness, economic growth, improved quality of life and sustainable development. These investments support the delivery of the Europe 2020 strategy.”2 In 2007-2013 approximately EUR 50 billion was allocated each year for regional policy, a third of the EU’s total budget. EU regional policy is implemented through structural funds. These include the European Regional Development Fund (ERDF), the European Social Fund (ESF), and the Cohesion Fund (CF).
Every EU region can benefit from the ERDF and the ESF. However, only the regions that have GDP per capita below 75% of the EU average are eligible for support from the Cohesion Fund. In the programming period 2007-2013, the ERDF outlays accounted for 58% of the EU regional policy contribution, while the ESF and the CF accounted for 22% and 20%, respectively3 .
The main goal of EU regional policy is to decrease income disparities between Member States. However, instead of pure income redistribution, the aim of the support measures is to enhance investments and achieve higher regional growth rates (Marzinotto 2012). For instance in the programming period 2007-2013, regional support in Northern Finland under the Regional Competitiveness and Employment Objective was allocated along three priority axes. The first of these priority axes is the promotion of business, which finances development and investment projects by start-ups and growth-oriented small and medium-sized enterprises. The second axis is the promotion of innovation, which supports various innovation and networking projects by universities, technology centers, and research institutions. The third priority axis is the improvement of the accessibility of areas, which finances infrastructure-related projects by municipalities, associations, and other public bodies. The total public financing of the ERDF programme for Northern Finland in 2007-2013 was EUR 600 million, of which the EU’s contribution was fifty percent.
Despite the significant budget outlays, scientific evidence of these programmes’ effectiveness is scarce. In a recent literature review, Mohl, Hagen (2010, p. 353) concluded that empirical evidence has provided mixed and contradictory results. One of the main reasons for this is the fact that the allocation of structural funds depends on economic outcomes: only poorer regions are eligible in the first place. Hence we have a situation of reverse causality, where it is difficult or impossible to identify the causal effects of the policy. Imprecise data, unobserved or omitted variables, and possible spillover effects also hinder identification. In a nutshell, we do not know much about the causal effects of regional policies.
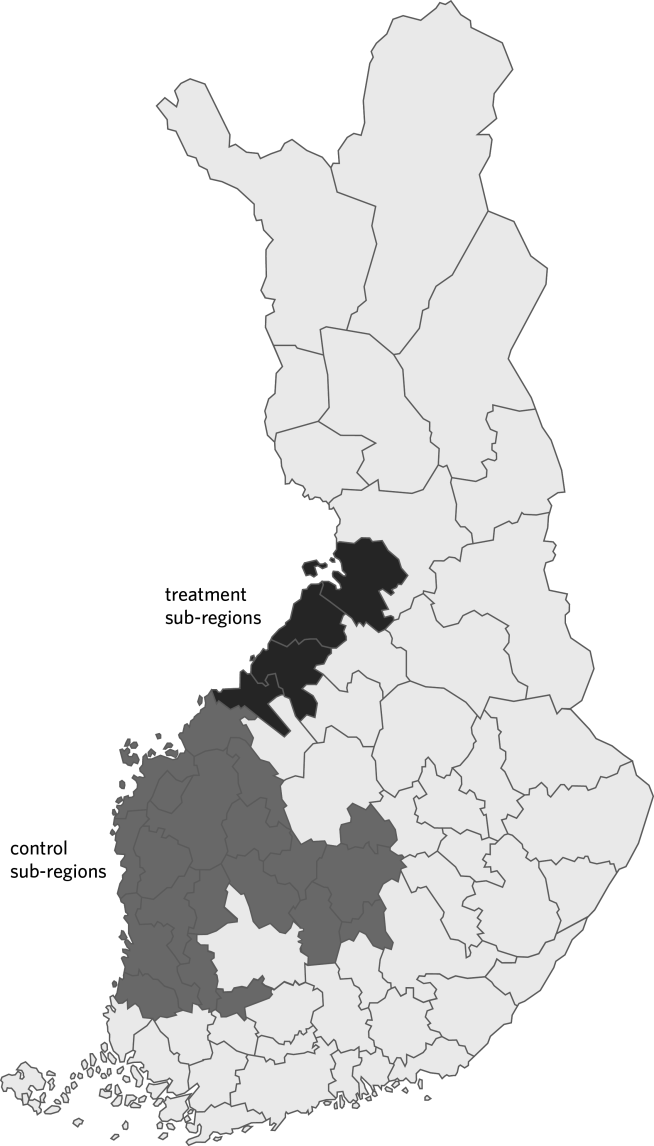
In an ideal situation, we would pick out regions at random, support those regions, and compare economic outcomes to non-supported regions, i.e. use a randomized controlled trial to estimate the causal effect. However, this is not possible in practice. As a next-best alternative, we should look for exogenous changes in programme eligibility, and whether these changes have created circumstances similar to randomization. One candidate for such an exogenous change occurred in Finland in 2007. For legislative reasons (explained in detail in Section 3), parts of regions previously covered by the ERDF Programme for Western Finland were reallocated to the ERDF Programme for Northern Finland. As support levels (EUR/capita) are much higher in Northern Finland, this change created a natural experiment where some regions received a windfall of support. The increase in regional support in the treatment areas was roughly EUR 20 million per year. Those areas within the ERDF programme for Western Finland that did not experience a change in their programme area status will be the control areas.
In this paper, we analyze the economic outcomes of this reallocation, using detailed postal code area data. Using difference-in-differences estimators, we found that the change in programme area status decreased the unemployment rate especially in those areas where the increase in regional support was the most pronounced. An increase in the number of jobs was also detected. However, we were unable to detect any effects on disposable income per capita or population with tertiary education. Our robustness checks included specification tests, pseudo-treatment analysis, and tests for spatial correlation.
The rest of the paper is organized as follows. Previous literature is reviewed in Section 2, followed by our research design in Section 3. Data and methods are detailed in Section 4, and estimation results are presented in Section 5. Various sensitivity and robustness checks are explained in Section 6. Section 7 concludes our discussion.
2 Previous literature
The economic theory of regional development has undergone drastic changes during the last six decades. Seminal work by Solow (1956) presented the neoclassical growth model, which states that constant returns to scale economies with access to the same technology approach steady state growth automatically. Market forces would therefore ensure income convergence of differing countries or regions and there is no need for regional policy. However, subsequent empirical observations raised fundamental questions about the validity of the neoclassical growth theory; convergence appeared to be much slower than the rate proposed by the theory (Martin, Sunley 1998, p. 220).
Current theories of agglomeration and economic geography are reviewed by Ottaviano, Thisse (2004). Transport costs play a pivotal role in agglomeration: firms are likely to cluster within large metropolitan areas when they sell differentiated products and transport costs are low. At the same time, cities provide a wide array of final goods and specialized labor markets that make them attractive to workers. However, the market can yield agglomeration even for those transport cost values for which it is socially desirable to keep economic activities dispersed. Hence there may be scope for regional policy interventions on both efficiency and equity grounds (Ottaviano, Thisse 2004).
Since its beginning, the EU has aimed at “reducing the disparities between the levels of development of the various regions”4 . The ERDF was established in 1975. New member states increased regional disparities in the 1980s and 1990s and regional funding was multiplied, as more countries became eligible for funding. Annual regional development projects were replaced by multi-annual programmes. Cohesion Fund measures were aimed at the regions with GDP per capita strictly below 75% of the EU average. ERDF measures were directed at other less developed, sparsely populated, or mountainous regions. Since 1989, there have been four completed programming periods: 1989-1993, 1994-1999, 2000-2006, and 2007-2013. The fifth programming period, 2014-2020, is ongoing.
In theory, ERDF support for small and medium-sized enterprises’ investments should increase economic activity in the recipient areas. Increased economic activity should create new jobs, lead to lower unemployment, and increase per capita income and economic growth. The official EU regional policy targets for the programming period 2007-2013 in Finland were:
- Create new enterprises and jobs to increase employment;
- Develop the regional economy;
- Increase the productivity, competitiveness and exports of enterprises;
- Raise the education level; and
- Increase research and innovation to 4% of GDP5 .
The thorough literature review by Mohl, Hagen (2010) summarizes sixteen previous empirical studies that analyzed the impact of structural funds on regional economic growth6 . Most authors have used regional panel data, mainly at the NUTS-2 level, and standard panel data estimators. Nomenclature of Units for Territorial Statistics (NUTS) is the EU standard for referencing the subdivisions of countries for statistical purposes. There are three NUTS levels. While some studies have included all available EU countries, others have concentrated on single countries. Only three papers have treated structural funds as an endogenous variable. The overall results are inconclusive: some papers have found positive effects, some zero effects, and some even negative effects on growth. Mohl, Hagen (2010) suggest that probable reasons for diverging results include poor data quality, differences in research designs, and unrealistic exogeneity assumptions.
Dall’erba, Le Gallo (2008) argue that the lack of positive regional policy effects may be due to several institutional factors. Funded projects may fulfil EU criteria but are not necessarily growth stimulating. This might even be intentional, for example if the regional governments aim to keep their region within the eligibility criteria for cohesion support. EU funding may also crowd out private investments in the area or the funded project is undertaken by a firm headquartered outside the targeted region. Furthermore, the principle of additionality requires that national funding at least equals EU support. According to Dall’erba, Le Gallo (2008), the wealthiest regions may provide 2.5-6.4 times the amount committed by EU structural funds and in the end, the total invested may be larger in the wealthiest regions.
Since the aforementioned review, Le Gallo et al. (2011) have performed local impact estimations, where one coefficient is estimated for each region. They utilize panel data from 145 NUTS-2 regions, covering the period 1989-1999. Global estimates for a typical region in Europe do not confirm positive effects on growth. However, using a locally linear spatial model, they estimate highly diverse local impacts, some positive, some negative. They recognize that significant negative impacts of structural funds may seem counterintuitive, and suggest possible explanations for this phenomenon, for instance long-term economic decline of these areas. Hence endogeneity problems are only mentioned and they are left for future research.
Becker et al. (2012) have analyzed panel data at the NUTS-3 level to estimate the effects of regional policy on growth. Using generalized propensity score estimation, they found that transfers enhance growth in the recipient regions. They also conclude that some reallocation of funds would lead to even higher aggregate growth in the EU. Becker et al. (2012) argue that in this case, selection bias is effectively reduced with the propensity score estimator.
Pellegrini et al. (2013) evaluate the effects of regional policy using the regression discontinuity design (RDD). They exploit the allocation rule of structural funds, namely that only regions with GDP less than 75% of EU average are eligible for Objective 1 support. In the regression discontinuity approach, estimation of causal effects is based on the assumption that regions just above the 75% threshold are very similar to those that are just below the 75% threshold. Using a regional dataset for 1994-2006, Pellegrini et al. (2013) found positive growth impacts from regional policy.
Becker et al. (2013) used regression discontinuity design and data on NUTS-2 regions to estimate the heterogeneity of Objective 1 treatment effects. They found that in general, the variance of the treatment effect is much larger than its mean. Only 30 percent of recipient regions are able to turn regional transfers into faster per capita income growth. According to Becker et al. (2013), success depends on the level of human capital and the quality of institutions in the recipient regions. Percoco (2016) and Gagliardi, Percoco (2016) employ similar RDD estimation strategies to explore the confounding effects of local economic structure and degrees of urbanization on cohesion policy effectiveness.
In a recent discussion paper, Breidenbach et al. (2016) study the spatial dynamics of structural funds using NUTS-2-level panel data. They observe negative indirect spatial effects that largely determine a negative overall effect of regional policy on growth. Breidenbach et al. conclude that EU structural funding does not seem to foster income convergence across regions.
Dall’erba, Fang (2017) produced a meta-regression analysis of the impact of structural funds on GDP growth. Their meta-analysis is based on 17 econometric studies which estimated cross-sectional beta-convergence models. The results indicate that several differences in the data characteristics are at the origin of the primary estimates’ heterogeneity. Controlling for endogeneity also has an impact on size of the estimates. In contrast, the differences in functional forms do not have a significant impact on the primary estimates.
Cross-sectional convergence models and, more recently, standard panel data estimators have been the mainstay of EU regional policy research. These allow for comparisons and meta-analysis, but endogeneity issues may be difficult to circumvent. Counterfactual (natural or quasi-experimental) approaches to causal inference have been rarely used, in part because suitable cases are scarce. Counterfactual methods may yield more credible estimates of the causal effects, but generalization of the results might be problematic.
Our contribution to the literature can be summarized as follows. To estimate the causal effect of regional policy on various economic outcomes, we exploit a natural experiment arising from an exogenous change in programme eligibility, using a highly detailed postal code area dataset.
3 Research design
Our research design is based on the ERDF programme area reallocation which occurred in Finland in 2007, in the beginning of the new programming period 2007-2013. Behind this reallocation were two recent changes in EU legislation. First, the legal framework for the NUTS classification was established with Council Regulation (EC) No 1059/20037 . The classification is outlined in Annex 1 of the Regulation. Secondly, the regulations for the new programming period 2007-2013 required that eligible programme areas follow the NUTS classification adopted four years earlier.
The implementation of the EU’s regional policy began in Finland in 1995, when it became a Member State of the EU. During the programming period 1994-1999 the EU’s Regional Policy Objectives 2, 5b, and 6 were implemented. During the programming period 2000-2006, Objectives 1, 2, and 3 were implemented8 . In 1995-2006, the largest urban areas (Helsinki, Turku, Tampere) were non-eligible for support, and in general, support levels increased the farther north or north-east a region was situated from the most populous regions of Southern Finland.
For the programming period 2007-2013, previous Regional Policy Objectives 1, 2, and 3 were replaced with the objectives: Regional Competitiveness and Employment; and European Territorial Cooperation. Council Regulation (EC) No 1083/20069 lays down general provisions on the Structural Funds for the period 2007-2013. Recital 16 of the Preamble explains that the identification of eligible areas should be based on the NUTS classification established by Regulation (EC) No 1059/2003. Furthermore, Article 6 regulates that each Member State is required to indicate the NUTS-1 or NUTS-2 level regions for which it will present a programme for financing by the ERDF.
In Finland the previous programme area allocation was based on the EU Accession Treaty, and this allocation did not comply with the NUTS classification. Finland therefore was obliged to alter the ERDF area allocation so that it matched the NUTS-2 regional division. There are four NUTS-2 regions – Southern, Western, Eastern and Northern Finland – and each had its own regional programme during 2007-2013. The largest reallocation took place in the region of Ostrobothnia in Western Finland. Four sub-regions previously included in the ERDF Programme for Western Finland were reallocated to the ERDF Programme for Northern Finland. The largest cities also became eligible for support but their support level is low when compared to the other regions.
The baseline year of our study is therefore 2007. At that time, Finland had 20 regions (maakunta). These regions were divided into 77 sub-regions (seutukunta). Each sub-region consists of two or more neighbouring municipalities, which create a joint employment area.
The area reallocation in Ostrobothnia is especially intriguing because the regional support intensities, measured in EUR per capita, are much higher in Northern Finland than in Western Finland. As a result, the reallocated Western Finland areas received a considerably higher level of support (EUR per capita) in the programming period 2007-2013 than in the previous programming period. Hence the change in programme area status created a natural experiment: since the cause for the change was exogenous, the situation is the same as if these reallocated areas were chosen randomly. As a counterfactual we can use those regions in Western Finland where the programme area status did not change (grey areas in Figure 1). These conditions allow us to estimate the causal effect of regional policy on various economic outcomes.
Of the total ERDF budget of EUR 600 million in Northern Finland for the programming period 2007-2013, 39% was allocated to development projects by start-ups and SMEs, 37% to innovation and networking projects, 20% to infrastructure projects, and 4% to technical support10 . Note that these are the three priority axes mentioned in the introduction. The idea is that these combined efforts together produce the desired results of the EU regional policy. In the short and medium run, support for start-ups and SMEs entail the largest new employment possibilities. The realized allocation of program funding naturally depends on the number and quality of the funding applications, as well as the local and regional priorities of the funding agencies.
The treatment and control areas in Figure 1 had two support categories during the previous programming period in 2000-2006. Objective 2 areas had a higher support intensity (EUR/capita) and so-called transitional areas had a lower support intensity. Transitional areas were areas that had been ERDF Objective 2 or Objective 5b areas during 1995-1999 but did not fulfil new Objective 2 criteria for the programming period 2000-2006. The increase in ERDF support resulting from the area status change in 2007 was largest among those treatment areas that had been transitional areas in 2000-2006 (Table 1). Their support intensity grew from 9.4 EUR/capita to 69.9 EUR/capita, approximately a sevenfold increase. In addition to support from the EU, regional policy programmes always include additional national support of at least the same amount as the EU provides.
| Treatment and | Control | Treatment | |
| Support category in 2000-2006 | control areas | areas | areas |
| 2000-2006 | 2007-2013 | 2007-2013 | |
| Objective 2 programme areas | 32.8 | 17.0 | 69.9 |
| Transitional areas | 9.4 | 17.0 | 69.9 |
Notes: Population data as of 1.1.2007
It should be noted that the support intensity changed in 2007 in the control areas as well. In the previous Objective 2 areas, ERDF support decreased, while among the previous transitional areas, support levels increased. However, the increase was minor compared to the treatment areas.
The treatment area is defined in our study as (1) the sub-regions of Kokkola and Ylivieska and the municipalities of Oulu and Hailuoto, which previously were Objective 2 areas; and (2) the sub-region of Raahe and the municipalities of Liminka, Lumijoki, Muhos, and Tyrnävä in the Oulu sub-region, which were previous transitional areas. Using population data from 2007, the approximate increase in regional support (EU + national) resulting from the area status change was roughly EUR 14.1 million per year in the previous Objective 2 areas and EUR 7.4 million per year in the previous transitional areas. Over the seven-year programming period, this amounts to an increase of EUR 150 million in regional support for the treatment areas.
4 Data and methods
In this Section we first describe our data set and then outline the econometric methodology. Since the treatment area is quite small (see Figure 1), sub-regional or municipality level data would be too coarse for our needs. The treatment area only includes four sub-regions11 and those sub-regions include 22 municipalities (13 in the previous Objective 2 area and 9 in the previous transitional area). Therefore we use more disaggregated postal code area data. This allows us to analyze 122 treatment area observations, with roughly 700 observations for the control areas. Statistical postal code areas are defined by Statistics Finland and they are based on addresses (postal codes) of firms, government offices and inhabitants. Each municipality has approximately ten postal code areas on average12 .
Our data set was obtained from Statistics Finland and it includes the following variables of statistical postal code areas from the years 2004-2013 (end of each year):
- number of inhabitants;
- share of inhabitants with tertiary education (%);
- unemployment rate (%);
- number of jobs in the area, all industries, part-time jobs included; and
- median disposable income per capita, CPI deflated.
Summary statistics of treatment and control postal code areas for the baseline year are presented in Table 2. Statistics are presented separately for the previous Objective 2 areas and the transitional areas. As a baseline year we use 2007, since the Finnish ERDF programmes were officially approved by the European Commission in September 2007, and their implementation began in late 2007.
Note that the ERDF support payments are not distributed equally to all postal code areas or municipalities in the recipient sub-regions. Postal code area division is used in this study solely to increase the available number of observations in the treatment and control areas.
| Variable | Control areas | Treatment areas
| ||||
| No. of | Mean | Std. dev. | No. of | Mean | Std. dev. | |
| postal | postal | |||||
| code | code | |||||
| areas | areas | |||||
| number of inhabitants | 440 | 1,398 | 2,218 | 82 | 2,754 | 2,937 |
| share of inhabitants with | 438 | 6.6 | 3.8 | 81 | 9.9 | 6.6 |
| tertiary education (%) | ||||||
| unemployment rate (%) | 422 | 9.9 | 3.9 | 81 | 9.2 | 3.8 |
| no. of jobs, all industries | 438 | 531 | 1,455 | 82 | 1,240 | 2,246 |
| median disposable | 438 | 16,658 | 2,561 | 81 | 18,120 | 2,512 |
| income, EUR/cap. | ||||||
| number of inhabitants | 272 | 1,326 | 2,057 | 40 | 1,485 | 1,757 |
| share of inhabitants with | 270 | 7.3 | 3.5 | 40 | 6.1 | 3.1 |
| tertiary education | ||||||
| unemployment rate | 267 | 5.6 | 2.8 | 39 | 9.9 | 4.0 |
| no. of jobs, all industries | 273 | 535 | 1,490 | 40 | 464 | 832 |
| median disposable | 270 | 17,864 | 2,417 | 40 | 18,448 | 2,487 |
| income, EUR/cap. | ||||||
Notes: Units of observation are statistical postal code areas.
In Table 2 we observe systematic differences between the treatment and control areas even before the intervention, especially among the previous Objective 2 areas, where the treatment areas are roughly double the size of the control areas. However, the unemployment rates are quite similar. In contrast, the previous transitional areas are comparable in size but have differing unemployment rates. In any case, straightforward statistical tests of the differences in outcomes are not feasible. Systematic differences first have to be accounted for, and this is accomplished using standard econometric methods.
Differencing between two time periods effectively removes unobservable time-invariant characteristics of the postal code areas, such as geographical size, location, distance to large cities, and so forth (Wooldridge 2010). There are also slowly changing variables, such as the demographic and business structure of the postal code area, that are approximately constant during the study period, 2007-2013. These are controlled for by differences as well.
We use two period panel data models throughout, with the year 2007 as the baseline (“before treatment”) year, and each one of the years 2008-2013 consecutively as the “after treatment” year. That is, our dependent variable is the difference in the outcome variable Y in 2007-2008, in 2007-2009, etc. Our simple difference-in-differences equation can be written as:
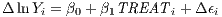
TREAT is equal to one if the postal code area was treated and zero otherwise. As usual, Δ denotes the difference. The coefficient of interest is β1.
Note that our methodological approach implicitly controls for a multitude of both observable (size, location, etc.) and unobservable (local economic traditions, etc.) time-constant variables. One major drawback is that we are unable to control for time-varying confounders. However, due to the experimental nature of our treatment, we have no reason to assume that these confounders would be systematically related to the treatment. Hence any positive or negative local random shocks that may affect for instance employment are lumped together in the error term. This has no effect on the consistency of our results, as the treatment is exogenous by construction.
Also note that using multiple years of panel data in our estimations would not yield more elaborate results but rather to the contrary. Since TREAT = 1 for all treatment areas and TREAT = 0 for all control areas during the whole study period, 2008-2013, its effect is indistinguishable from the fixed effect for each area. Including “before treatment” years (2006, 2007 for instance) in the FE regressions would allow for treatment effect estimation, but the coefficient would then measure the average of the treatment effect across multiple years. Hence our simple two-period approach (before-after) is in fact a more versatile tool in this case. But it also necessitates the use of disaggregated regional data in order to obtain a reasonable number of observations. As mentioned above, the treatment area only includes 22 municipalities.
| Europe 2020 Strategy | EU Regional Policy targets for | Related outcome variables in |
| targets | Finland during 2007-2013 | this study |
| Increase employment | Create new enterprises and jobs | Number of jobs. |
| rate | to increase employment. Develop | Unemployment rate. |
| the regional economy. Increase | Disposable income per capita | |
| the productivity, competitiveness | ||
| and exports of enterprises | ||
| Increase research and | Increase research and innovation | —
|
| development | ||
| Reduce greenhouse | — | —
|
| gas emissions | ||
| Improve tertiary | Raise the education level | Share of inhabitants with |
| education levels | tertiary education | |
| Reduce poverty | Develop the regional economy | Disposable income per capita |
The crucial assumption in order for the difference-in-differences estimates to be valid is that of common or parallel trends (Meyer 1995, Abadie 2005). Before the treatment, control and treatment units should exhibit a similar trend in the outcome variable. In essence, the control group has to be a convincing counterfactual for the treatment group, and therefore we should observe parallel development ex ante. Common trend assumption can be tested using pre-treatment observations, and in this case, we use postal code area data from the years 2004-2007. If the parallel trend assumption fails, we do not have a credible counterfactual.
Since the Europe 2020 growth strategy has no specific population targets, as outcome variables we use the following:
- share of inhabitants with tertiary education;
- number of jobs;
- unemployment rate; and
- median disposable income per capita.
Outcome variables have been transformed to natural logarithms before taking differences. Results are unweighted and estimated using municipality-clustered standard errors, as observations from the same municipality might be correlated due to municipality level employment policies and decisions.
We use the exogenous treatment dummy as the sole regressor, since including other outcome variables as controls would require considerably more complicated methods. Both the Europe 2020 Strategy and the EU Regional Policy have multiple goals. As most of these goals are not measured at the postal code area level, we are forced to use the best available proxies in our analysis. For instance, GDP growth or poverty levels are not available, so we use disposable income as a proxy for both. Table 3 underlines the linkages between our outcome variables, the EU2020 targets, and EU Regional Policy targets for Finland. Note that the policy targets concerning the R&D outlays or greenhouse gas emissions are left for future research as there are no data or relevant proxy variables available.
5 Results
Our difference-in-differences estimation results for four outcome variables and six different treatment periods are presented in Table 4. Panel A includes results for those treatment and control areas that were Objective 2 areas in 2000-2006, and Panel B includes results for those treatment and control areas that were transitional areas in 2000-2006. The results of three different comparison periods are also presented in Table 4. Each entry in the table is the estimated coefficient for the treatment dummy. For brevity, constants and other summary statistics, except for the coefficients of determination (which are denoted as R2), are omitted and are available on request.
Results are presented separately for the previous Objective 2 areas and the transitional areas, as the relative change in support intensity in 2007 was distinctly different in those areas (Table 1). In the previous Objective 2 areas ERDF support approximately doubled, whereas in the previous transitional areas ERDF support increased sevenfold.
The number of observations in the four outcome equations for each period is indicated in the first column of Table 4. We have approximately 500 postal code area observations for the previous Objective 2 areas and approximately 300 observations for the previous transitional areas.
The results can be summarized as follows. In Panel A of Table 4 we find no evidence of regional policy effectiveness. The income per capita equation yields mainly negative coefficients, though only two comparison periods (2004-2005 and 2004-2007) are statistically significant. How do we interpret this result? Table 2 indicates that by chance, the median disposable income per capita was lower among the control areas (EUR 16,600) than in the treatment areas (EUR 18,100) in 2007. Therefore, even before the treatment, disposable incomes in the control regions converged towards the income levels of the treatment regions. Similar convergence has seemingly continued after the treatment (p-value for the period 2007-2013 is 0.11). Hence what Table 4 suggests is that there has been micro-level income convergence that seems to be unrelated to the EU regional policy.
In Panel B of Table 4 we do find some evidence of regional policy effectiveness. The unemployment rate has decreased in the treatment areas in all six treatment periods after 2007. We observe no differences in the previous three comparison periods, i.e. before the treatment. We also detect a significant increase in the number of jobs for the period 2007-2012. The coefficient for the longest period 2007-2013 in the jobs equation is also borderline significant (p = 0.083). Due to insignificant coefficients of the earlier periods, the evidence of policy impact on total jobs is not as strong as the impact on unemployment. We find no evidence of regional policy effects on tertiary education or income per capita.
Policy impact on unemployment is illustrated in Figure 2, which depicts the mean of logarithmic unemployment rate for the years 2004-2013 in the treatment and control sub-regions located in the previous transitional areas (i.e. Panel B of Table 4). The area reallocation year (2007) is marked with a vertical reference line. Immediately after 2007, unemployment starts to increase in the control sub-regions. Additionally, from 2007 to 2009 – due to the global financial crisis – unemployment increases are much more pronounced in the control sub-regions than in the treatment sub-regions. Also in the longer run, 2007-2013, the relative increase in unemployment is larger in the control sub-regions than in the treatment sub-regions. In contrast, Figure 3 depicts the case of no impacts (i.e. Panel A of Table 4), where the treatment and control sub-regions move roughly in unison.
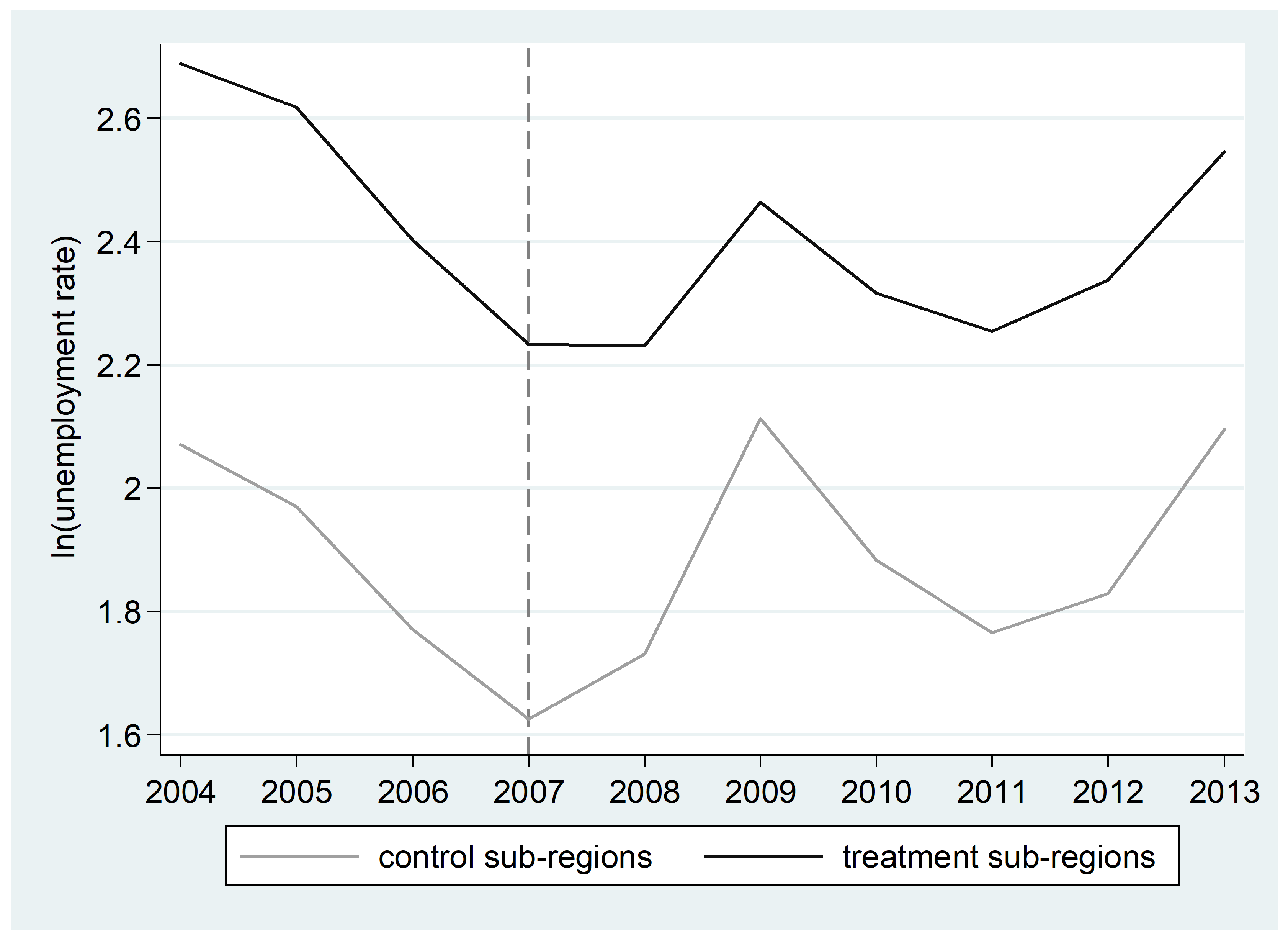
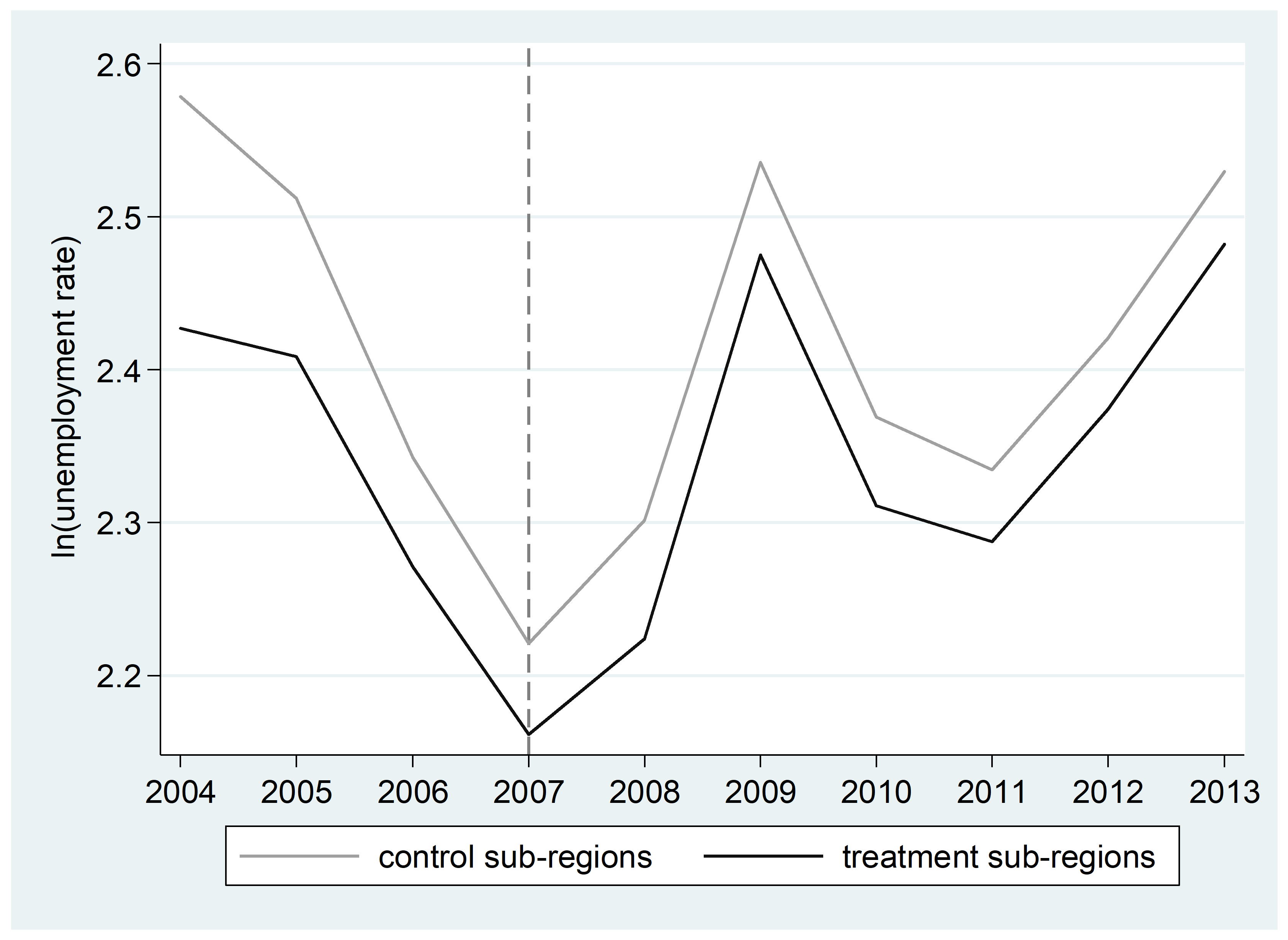
Unemployment rate coefficients in Panel A and Panel B of Table 4 are markedly different. We tested whether this could be due to differing population sizes of control and treatment areas in Panel A by using a trimmed control group, which included only those postal code areas with 500 or more inhabitants (with the trimming, the mean population of control areas is 2,807). This did not have an effect on the results. We conclude that the difference in coefficients may reflect the unequal relative changes in ERDF support intensity: support per capita increased by 113% in Panel A treatment areas, and by 644% in Panel B treatment areas.
In Panel B, why do we observe policy effects only in some outcome variables? When the year-to-year relative changes are small, differences in those changes are difficult to detect. It is instructive to assess the relative changes in our outcome variables after the 2008 global financial crisis. From 2007 to 2009, the total number of jobs in the Finnish economy, part-time jobs included, decreased from 2.21 million to 2.11 million, i.e. a decrease of approximately five percent. Despite the recession, disposable income per capita in fact increased by four percent during the same time13 . The share of population with a tertiary education increased from 12.7% to 13.9% – an increase of 1.2 percentage points, or a relative change of 9%. The unemployment rate increased from 8.3% to 11.4%, an increase of 3.1 percentage points, or a relative change of 37%.
When these relative changes are compared, we find that the unemployment rate is easily the most volatile among our outcome variables. Therefore when treatment and control areas are compared, possible differences in the unemployment rate changes are easier to detect. Another possibility is that the regional policy measures through the ERDF do not in fact have an effect on some outcome variables. As mentioned above, of the Northern Finland ERDF support for 2007-2013, 39% was allocated to development and investment projects by start-ups and SMEs, 37% to innovation and networking projects, 20% to infrastructure projects, and 4% to technical support. Research institutions and schools engage in innovation and networking projects, while infrastructure projects mainly consist of various transport-related investments that the municipalities are undertaking.
Analyzing the allocation of ERDF support funding suggests that the support measures could in principle have an effect on the number of jobs, unemployment and even income per capita in the treatment regions. However it is questionable whether these measures succeed in increasing the share of population with tertiary education. It appears that reaching this target would require somewhat different support allocation.
Naturally, regional policies could also have effects which take place years after the support programme ended. Our data only covers the programming period in question, i.e. 2007-2013. Unfortunately, we cannot evaluate the long-term effects of the programme, as the next EU programming period 2014-2020 followed immediately after the previous programme concluded. It is probable that the estimated employment effects are at least partly explained by the supported projects’ personnel and are therefore temporary.
5.1 Possible complications
Finnish postal code areas may cross municipal boundaries or lie within a single municipality. However, all postal code areas in the data are assigned to one municipality only on the basis of largest population shares14 . Especially large municipalities sometimes have their own local policies to reduce unemployment and increase employment in their area. Due to collinearity, we cannot use municipality dummies as this would render the treatment dummy obsolete. Furthermore, note that the location of the postal code area (in municipality j) is controlled for by differencing, and if we assume that municipality-level employment policies are more or less fixed during the study period, those policies are controlled for as well. However, postal code areas in a single municipality might be correlated, and this is accounted for by using clustered standard errors in Table 4.
In recent years, there have been many municipality mergers in Finland, and the number of municipalities has declined from roughly 450 at the beginning of the new millennium to 320 in the year 2013. An especially large merger wave occurred in 2009 when 67 municipalities were merged. Behind these mergers is usually poor economic performance of the merging municipalities and the need for cost savings. In the next section we analyze the possible effect of municipality mergers and similar confounding issues that might have an effect on our results.
Possible displacement effects might be another complication. In a recent discussion paper, Einiö, Overman (2016) study the displacement effects of spatially targeted enterprise initiatives using detailed spatial data. They conclude that the observed positive employment effects close to the eligible area boundaries were offset by negative employment effects just outside the programme area. The unintended displacement of economic activity across the treatment area boundary is problematic and merely shifts employment from one deprived area to another. Their study also suggests that local displacement effects could cause bias when estimating the impacts of regional policy, even in the case of random area assignment.
However, in our data, the treatment and control areas are not neighbouring areas when we analyze previous transitional areas (Panel B of Table 4). Sub-regions bordering on the treatment area are either previous Objective 2 areas, which also experienced an increase in ERDF support (reaching the same level per capita as the previous transitional areas), or the original Northern Finland sub-regions, which had higher ERDF support per capita to begin with. Therefore it is unlikely that local displacement effects cause significant bias in our results.
Spatial correlation is another complication which could cause bias in difference-in-differences estimators (Delgado, Florax 2015). The importance of spatial effects in regional policy analysis was introduced by Dall’erba, Le Gallo (2008). In the case of spatial correlation, the observations are not independent, but the outcome of area i depends on the treatment status of a neighbouring area j (whether in the same municipality or not). This issue is also addressed in the next Section.
6 Robustness checks
To assess the robustness of our results in Table 4, we first take a closer look at the municipality mergers of 2009. It is possible that municipality mergers have affected treatment and control areas differently, and this has had an effect on the results. Secondly, we analyze the confounding effects of so-called abrupt structural changes, where a sub-region has experienced a sudden mass layoff caused by the closure of a paper mill or a similar negative shock. As a third robustness check, we conduct a pseudo-treatment and compare the results to previous estimates. Fourthly, we estimate selected spatial regressions and discuss the effects of spatial correlation.
6.1 Municipality mergers of 2009
As mentioned above, the year 2009 saw a record number of municipality mergers, 67 in total. Some of those mergers took place in the treatment and control areas of this study. We therefore create a dummy variable merger, which equals one if the postal code area was located in a municipality that merged in 2009, and zero otherwise. We then use this dummy variable as an additional regressor in the 72 equations presented in Table 4.
Of the 72 re-estimated equations, only two equations (2.8%) yield a statistically significant coefficient for the merger variable at the 0.05 significance level15 . In neither case is the treatment coefficient noticeably different from the previous estimates. We therefore conclude that it is unlikely that municipality mergers would be driving our results. Note that the merger dummy could be endogenous if for instance previous disappointing unemployment or income levels caused mergers. In this case we should observe significant merger coefficients in the pre-treatment periods, as merger processes may take two to three years to complete. However, none of those coefficients are significant.
6.2 Abrupt structural changes
Areas of abrupt structural change16 are sub-regions (or single municipalities) that the government subsidizes more heavily for a fixed period of two or three years. These areas have experienced a sudden negative shock, such as the closure of a paper mill, which is expected to increase unemployment sharply. It is possible that this negative effect or the extra subsidies for these areas are confounding factors in our equations.
In our study period and area, there have been only two specially designated structural change areas: the sub-region of Rauma in 2013 and the sub-region of Oulu in 2012-2013. The sub-region of Rauma was part of the previous Objective 2 areas and belonged to the control group. The sub-region of Oulu was in the treatment group and included both previous Objective 2 and transitional areas.
Therefore, we include a structural change area dummy variable in the respective regressions, and re-estimate the job and unemployment equations. In the case of previous Objective 2 areas, we get the same result as in Table 4: no effect. In the case of previous transitional areas, we observe that allowing for the adverse effects of Nokia-related layoffs in the Oulu region has quite a logical effect on the results: we see larger regional policy effects. In Table 5 we present the estimates for the job and unemployment equations for the time periods 2007-2012 and 2007-2013.
| independent | ln(jobs) | ln(jobs) | ln(unemploy- | ln(unemploy- |
| variable | 2007-2012 | 2007-2013 | ment rate) | ment rate) |
| 2007-2012 | 2007-2013 | |||
| treat | 0.190* | 0.216 | -0.160** | -0.182*** |
| (0.075) | (0.122) | (0.059) | (0.048) | |
| structural change | -0.124 | -0.159 | 0.163 | 0.038 |
| area | (0.080) | (0.133) | (0.085) | (0.076) |
| constant | 0.018 | -0.009 | 0.218*** | 0.484*** |
| (0.038) | (0.037) | (0.033) | (0.034) | |
In the job equation, the structural change area dummy yields negative coefficients, although they are not significant (the p-values are 0.1-0.2). In the unemployment equation we find that Nokia-related layoffs have increased the unemployment rate, which is not surprising. Controlling for these mass layoffs yields larger coefficients for the treatment. In other words, the treatment is decreasing unemployment as desired, but if we do not control for the mass layoffs in the Oulu sub-region, coefficients for 2007-2012 and 2007-2013 are slightly biased downwards.
6.3 Pseudo-treatment effects
One way to test the robustness of results concerning policy effectiveness is to conduct a pseudo-treatment. That is, we choose a treatment region that was not treated in reality, and compare the effects of the “treatment” to a similar control group as the one used before. In this case, we should not see any statistically significant differences between treatment and control areas, except for some random variation.
For the pseudo-treatment we randomly choose two sub-regions from the previous transitional areas: the sub-region of Lounais-Pirkanmaa and the sub-region of Luoteis-Pirkanmaa. They contain 55 postal code areas in total. Note that in Panel B of Table 4, both sub-regions are control areas. The rest of the Table 4 control areas are used as controls in the pseudo-treatment case. The results are presented in Appendix, Table A1. Comparing the results to those in Table 4, we observe a notable difference, especially in columns 2 (number of jobs) and 4 (unemployment rate). Our pseudo-treatment is not producing the same effects as the real treatment.
6.4 Spatial correlation
In order to estimate spatial correlations, we obtained the X- and Y-coordinates of the geographic centers of postal code areas from Statistics Finland. We restrict our spatial analysis to the unemployment rate equations for the transitional areas (Panel B of Table 4), i.e. the only outcome variable which portrayed statistically significant results. First we created the row-standardized inverse distance weights matrix, using a distance band of 0-30 kilometers17 . For each period, we then measured the degree of global spatial autocorrelation with the Moran’s I measure. Finally we estimated the spatial lag models using the inverse distance weights matrix18 . Results are presented in Table 6.
| no. of observations | Moran’s I | unemployment rate | ||
| Treatment period: | ||||
| 2007-2008 | 299 | 0.007 | -0.115* | |
| (0.049) | ||||
| 2007-2009 | 299 | 0.124*** | -0.168* | |
| (0.069) | ||||
| 2007-2010 | 299 | 0.062** | -0.138** | |
| (0.048) | ||||
| 2007-2011 | 299 | 0.036 | -0.112* | |
| (0.054) | ||||
| 2007-2012 | 297 | 0.064** | -0.085 | |
| (0.049) | ||||
| 2007-2013 | 297 | 0.063** | -0.133** | |
| (0.048) | ||||
| Comparison period: | ||||
| 2004-2005 | 305 | 0.018 | 0.018 | |
| (0.039) | ||||
| 2004-2006 | 305 | -0.003 | 0.007 | |
| (0.044) | ||||
| 2004-2007 | 301 | 0.037 | -0.003 | |
| (0.052) | ||||
We do find evidence of spatial correlation in some of the treatment periods, and the regression coefficients of those periods are somewhat smaller when compared to the standard difference-in-differences estimates of Table 4. Note that the spatial regression coefficient for the 2007-2012 period is also borderline significant (p = 0.084). We therefore conclude that while spatial correlation is clearly causing non-negligible upward bias to our original results, the bias is not large enough to change our interpretation of the results. That is, the treatment decreased unemployment in the transitional areas.
On the basis of our robustness checks, our main results presented in Table 4 appear robust enough. In the concluding section the findings are summarized and possible caveats of the study design are highlighted. Directions for future research are also suggested.
7 Conclusions
We evaluated the causal effects of EU regional policy on key economic variables using a detailed postal code area dataset and difference-in-differences regression. Our study contributes to the current EU regional policy debate as it is based on a rare natural experiment setting. For legislative reasons, some Western Finland ERDF support areas were reallocated to the programme for Northern Finland in the beginning of the programming period 2007-2013. This change created favorable conditions for a ERDF programme evaluation because ERDF support intensities, measured as EUR per capita, are much higher in the northern regions. Overall, the use of quasi-experimental methods has been remarkably scarce in regional policy evaluations.
Regarding the Europe 2020 Strategy targets listed in the introduction, our results suggest that the regional policy of the European Union has had at least some beneficial effects. The ERDF programme has managed to decrease unemployment, which to a certain extent also helps to achieve Europe 2020 employment targets. An increase in the number of jobs was also observed. Therefore regional policy is not totally without merits. However, we are unable to detect any effects on tertiary education, for instance. Increasing the share of population with higher education is one of the main targets of the Europe 2020 strategy. To achieve all long-term growth strategy targets, other instruments besides regional policy are also needed.
The case under scrutiny is restricted to a certain geographic area in Western Finland and a fixed time period. As is always the case in empirical studies, one could argue that the results obtained are specific to this area and time period and they are not generalizable as such. Our view is that the study design allows for a careful generalization, at least to a degree. The analyzed intervention area was the result of two unrelated incidents, namely the Finnish EU Accession Treaty negotiations in 1994 and the establishment of a common classification of EU regional units for statistics a decade later. Hence the study design is as close to randomization as possible. Our robustness checks allow for alternative specifications, pseudo-treatments, and spatial correlation.
One major drawback of our study is that we are unable to analyze the long-term effects of regional policy. This would require the complete removal of regional aid for a period of several years, so that we could observe the development of key economic variables in its absence. Unfortunately, a “development without aid” scenario is not observable, as the programming period 2007-2013 was immediately followed by the current programming period 2014-2020.
The future research agenda should also include similar study designs from other EU member states. It is highly probable that analogous changes in programme eligibility areas have occurred elsewhere as well. Likewise the availability of highly detailed regional data is bound to improve in the coming years.
References
Abadie A (2005) Semiparametric difference-in-differences estimators. Review of Economic Studies 72: 1–19. CrossRef.
Becker S, Egger P, von Ehrlich M (2010) Going NUTS: The effect of EU structural funds on regional performance. Journal of Public Economics 94: 578–590. CrossRef.
Becker S, Egger P, von Ehrlich M (2012) Too much of a good thing? On the growth effects of the EU’s regional policy. European Economic Review 56: 648–668. CrossRef.
Becker S, Egger P, von Ehrlich M (2013) Absorptive capacity and the growth and investment effects of regional transfers: A regression discontinuity design with heterogeneous treatment effects. American Economic Journal: Economic Policy 5: 29–77. CrossRef.
Breidenbach P, Mitze T, Schmidt CM (2016) EU structural funds and regional income convergence – A sobering experience. Ruhr economic papers no. 608
Dall’erba S, Fang F (2017) Meta-analysis of the impact of European Union structural funds on regional growth. Regional Studies 51: 822–832. CrossRef.
Dall’erba S, Le Gallo J (2008) Regional convergence and the impact of European structural funds over 1989-1999: A spatial econometric analysis. Papers in Regional Science 87: 219–244. CrossRef.
Delgado MS, Florax RJGM (2015) Difference-in-differences techniques for spatial data: Local autocorrelation and spatial interaction. Economics Letters 137: 123–126. CrossRef.
Einiö E, Overman H (2016) The (displacement) effects of spatially targeted enterprise initiatives: Evidence from UK LEGI. VATT Institute for Economic Research, working papers 71/2016
Gagliardi L, Percoco M (2016) The impact of European cohesion policy in urban and rural regions. Regional Studies 51: forthcoming. CrossRef.
Le Gallo J, Dall’erba S, Guillain R (2011) The local versus global dilemma of the effects of structural funds. Growth and Change 42: 466–490. CrossRef.
Martin R, Sunley P (1998) Slow convergence? The new endogenous growth theory and regional development. Economic Geography 74: 201–227. CrossRef.
Marzinotto B (2012) The growth effects of EU cohesion policy: A meta-analysis. Bruegel Working Paper, No. 2012/14
Meyer B (1995) Natural and quasi-experiments in economics. Journal of Business and Economic Statistics 13[2]: 151–161. CrossRef.
Mohl P, Hagen T (2010) Do EU structural funds promote regional growth? New evidence from various panel data approaches. Regional Science and Urban Economics 40: 353–365. CrossRef.
Ottaviano G, Thisse JF (2004) Agglomeration and economic geography. In: Henderson V, Thisse JF (eds), Handbook of Regional and Urban Economics, Volume IV. Elsevier, Amsterdam, 2563–2608. CrossRef.
Pellegrini G, Terribile F, Tarola O, Muccigrosso T, Busillo F (2013) Measuring the effects of European regional policy on economic growth: A regression discontinuity approach. Papers in Regional Science 92: 217–233. CrossRef.
Percoco M (2016) Impact of European cohesion policy on regional growth: Does local economic structure matter? Regional Studies: forthcoming. CrossRef.
Solow R (1956) A contribution to the theory of economic growth. The Quarterly Journal of Economics 70: 65–94. CrossRef.
Wooldridge JM (2010) Econometric Analysis of Cross Section and Panel Data (2nd ed.). MIT Press, Cambridge
Appendix
| period | no. of | no. of jobs, | share of | unemploy- | median |
| observations | all industries | inhabitants | ment rate | disposable | |
| (min.–max.) | with tertiary | income | |||
| education | EUR/cap. | ||||
| Treatment period:
| |||||
| 2007–2008 | 260–272 | 0.024 | -0.013 | -0.047 | -0.010 |
| (0.026) | (0.020) | (0.067) | (0.006) | ||
| 2007–2009 | 260–273 | 0.017 | -0.010 | -0.131 | -0.004 |
| (0.045) | (0.017) | (0.065) | (0.011) | ||
| 2007–2010 | 260–273 | -0.064 | -0.024 | -0.017 | 0.001 |
| (0.053) | (0.029) | (0.066) | (0.008) | ||
| 2007–2011 | 260–273 | -0.017 | -0.033 | -0.114 | -0.001 |
| (0.046) | (0.031) | (0.078) | (0.010) | ||
| 2007–2012 | 258–273 | -0.002 | -0.024 | -0.082 | 0.011 |
| (0.055) | (0.032) | (0.078) | (0.010) | ||
| 2007–2013 | 258–273 | -0.036 | -0.020 | 0.062 | 0.009 |
| (0.064) | (0.035) | (0.073) | (0.010) | ||
| Comparison period:
| |||||
| 2004–2005 | 266–271 | 0.033 | 0.010 | 0.030 | 0.006 |
| (0.075) | (0.023) | (0.039) | (0.005) | ||
| 2004–2006 | 266–272 | -0.025 | -0.007 | -0.051 | 0.000 |
| (0.080) | (0.015) | (0.053) | (0.005) | ||
| 2004–2007 | 262–272 | -0.015 | 0.004 | -0.074 | 0.003 |
| (0.080) | (0.026) | (0.085) | (0.009) | ||
 © 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
© 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)