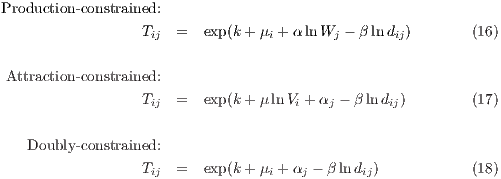Volume
3, Number 2, 2016, R11–R23 journal homepage:
region.ersa.org
Volume
3, Number 2, 2016, R11–R23 journal homepage:
region.ersa.orgDOI: 10.18335/region.v3i2.175
A primer for working with the Spatial Interaction modeling (SpInt) module in the python spatial analysis library (PySAL)
1 Arizona State University, Tempe, AZ, USA (email: toshan@asu.edu) Received: 6 November 2016/Accepted: 7 November 2016Abstract. Although spatial interaction modeling is a fundamental technique to many geographic disciplines, relatively little software exists for spatial interaction modeling and for the analysis of flow data. This applies particularly to the realm of free and open source software. As a result, this primer introduces the recently developed spatial interaction modeling (SpInt) module of the python spatial analysis library (PySAL). The underlying conceptual framework of the module is first highlighted, followed by an overview of the main functionality, which will be illustrated using migration data. Finally, some future additions are discussed.
1 Introduction
Spatial interaction modeling involves the analysis of flows from an origin to a destination, either over physical space (i.e., migration) or through abstract space (i.e., telecommunication). Despite being a fundamental technique to many geographic disciplines, there is relatively little software available to carry out spatial interaction modeling and the analysis of flow data, especially in the realm of free and open source software. Therefore, the purpose of this primer is to provide an overview of the recently developed spatial interaction modeling (SpInt) module1 of the python spatial analysis library (PySAL)2 . First, the current framework of the module will be highlighted. Next, the main functionality of the module will be illustrated using migration flows with a dataset previously used for spatial interaction modeling tutorials in the R programming environment (Dennett 2012). Finally, some future additions are discussed.
2 The SpInt framework
2.1 Modeling framework
The core purpose of the SpInt module is to provide the functionality to calibrate spatial interaction models. Since the “family” of spatial interaction models put forth by Wilson (1971) are perhaps the most popular, they were chosen as the starting point of the module. Consider the basic gravity model (Fotheringham, O’Kelly 1989),
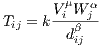 | (1) |
where
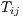 is an
is an 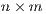 matrix of flows between
matrix of flows between 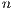 origins (subscripted by
origins (subscripted by 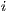 ) to
) to
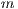 destinations (subscripted by
destinations (subscripted by 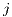 )
)
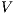 is an
is an 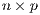 and vector of
and vector of 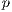 origin attributes describing the emissiveness
of
origin attributes describing the emissiveness
of 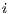
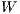 is an
is an 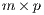 vector of
vector of 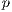 destination attributes describing the attractiveness
of
destination attributes describing the attractiveness
of 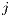
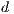 is an
is an 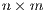 matrix of the costs to overcome the physical separation between
matrix of the costs to overcome the physical separation between
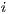 and
and 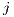 (usually distance or time)
(usually distance or time)
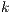 is a scaling factor to be estimated to ensure the total observed and predicted
flows are consistent
is a scaling factor to be estimated to ensure the total observed and predicted
flows are consistent
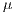 is a
is a 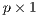 vector of parameters representing the effect of
vector of parameters representing the effect of 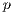 origin attributes
on flows
origin attributes
on flows
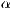 is a
is a 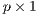 vector of parameters representing the effect of
vector of parameters representing the effect of 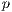 destination
attributes on flows
destination
attributes on flows
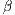 is a parameter representing the effect of movement costs on flows.
is a parameter representing the effect of movement costs on flows.
When data for 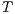 ,
, 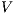 ,
, 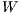 , and
, and 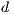 are available we can estimate the model
parameters (also called calibration), which summarize the effect that each model
component contributes towards explaining the system of known flows (
are available we can estimate the model
parameters (also called calibration), which summarize the effect that each model
component contributes towards explaining the system of known flows (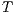 ). In contrast,
known parameters can be used to predict unknown flows when there are deviations in
model components (
). In contrast,
known parameters can be used to predict unknown flows when there are deviations in
model components (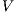 ,
, 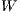 , and
, and 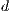 ) or the set of locations in the system are
altered.
) or the set of locations in the system are
altered.
Using an entropy-maximizing framework, Wilson derives a more informative and flexible “family” of four spatial interaction models (Wilson 1971). This framework seeks to assign flows between a set of origins and destinations by finding the most probable configuration of flows out of all possible configurations, without making any additional assumptions. By using a common optimization problem and including information about the total inflows and outflows at each location (also called constraints), the following “family” of models can be obtained,
where
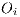 is an
is an 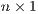 vector of the total number of flows emanating from origin
vector of the total number of flows emanating from origin 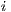
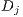 is an
is an 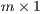 vector of the total number of flows terminating at destination
vector of the total number of flows terminating at destination
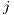
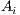 is an
is an 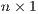 vector of the origin balancing factors that ensures the total
out-flows are preserved in the predicted flows
vector of the origin balancing factors that ensures the total
out-flows are preserved in the predicted flows
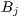 is an
is an 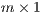 vector of the destination balancing factors that ensures the
total in-flows are preserved in the predicted flows
vector of the destination balancing factors that ensures the
total in-flows are preserved in the predicted flows
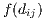 is a function of cost or distance, referred to as the distance-decay function.
Most commonly, this is an exponential or power function given by,
is a function of cost or distance, referred to as the distance-decay function.
Most commonly, this is an exponential or power function given by,
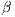 is expected to take a negative value. Different distance-decay functions assume
different responses to the increasing costs associated with moving to more distant locations.
Of note is that the unconstrained model with a power function distance-decay is
equivalent to the basic gravity model in equation (2), except that the scaling factor,
is expected to take a negative value. Different distance-decay functions assume
different responses to the increasing costs associated with moving to more distant locations.
Of note is that the unconstrained model with a power function distance-decay is
equivalent to the basic gravity model in equation (2), except that the scaling factor,
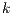 , is not included. In fact, there is no scaling factor in any of the members of the
family of maximum entropy models because there is a total trip constraint implied in
their derivation and subsequently their calibration (Fotheringham, O’Kelly 1989).
Another aside is that in the doubly-constrained maximum entropy model, the values
for
, is not included. In fact, there is no scaling factor in any of the members of the
family of maximum entropy models because there is a total trip constraint implied in
their derivation and subsequently their calibration (Fotheringham, O’Kelly 1989).
Another aside is that in the doubly-constrained maximum entropy model, the values
for 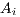 and
and 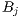 are dependent upon each other and may need to be computed
iteratively depending on calibration technique. It is also usually assumed that all
locations are both origins and destinations (i.e.,
are dependent upon each other and may need to be computed
iteratively depending on calibration technique. It is also usually assumed that all
locations are both origins and destinations (i.e., 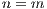 ) for doubly-constrained
models.
) for doubly-constrained
models.
Each member of the family of models provides a different system structure, which can be chosen depending on the available data or the specific research question at hand. The so-called unconstrained model does not conserve the total inflows or outflows during parameter estimation. The production-constrained and attraction-constrained models conserve either the number of total inflows or outflows, respectively, and are therefore useful for building models that allocate flows either to a set of origins or to a set of destinations. Finally, the doubly-constrained model conserves both the inflows and the outflows at each location during model calibration. The quantity of explanatory information provided by each model is given by the number of parameters it provides. As such, the unconstrained model provides the most information, followed by the two singly-constrained models, with the doubly-constrained model providing the least information. Conversely, the model’s predictive power increases with higher quantities of built-in information (i.e. total in or out-flows) so that the doubly-constrained model usually provides the most accurate predictions, followed by the two singly-constrained models, and the unconstrained model supplying the weakest predictions (Fotheringham, O’Kelly 1989).
2.2 Calibration framework
Spatial interaction models are often calibrated via linear programming, nonlinear optimization, or, increasingly more often, through linear regression. Given the flexibility and extendability of a regression framework it was chosen as the primary model calibration technique within the SpInt module. By taking the natural logarithm of both sides of a spatial interaction model, say the basic gravity model, it is possible to obtain the so-called log-linear or log-normal spatial interaction model,
where
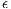 is a normally distributed error term with a mean of 0. The only difference between
equations (12) and (13) is the functional distance-decay specification, which results from
plugging either equation (10) for a power function or (11) for an exponential function
into equation (2) before linearizing it. The only practical difference here is that the
distance is logged in equation (12) whereas in equation (13) it is not. Constrained
spatial interaction models can be achieved by including fixed effects for the origins
(production-constrained), fixed effects for the destinations (attraction-constrained) or both
(doubly-constrained). However, there are several limitations of the log-normal gravity model,
which include,
is a normally distributed error term with a mean of 0. The only difference between
equations (12) and (13) is the functional distance-decay specification, which results from
plugging either equation (10) for a power function or (11) for an exponential function
into equation (2) before linearizing it. The only practical difference here is that the
distance is logged in equation (12) whereas in equation (13) it is not. Constrained
spatial interaction models can be achieved by including fixed effects for the origins
(production-constrained), fixed effects for the destinations (attraction-constrained) or both
(doubly-constrained). However, there are several limitations of the log-normal gravity model,
which include,
- 1.
- flows are often counts of people or objects and should be modeled as discrete entities;
- 2.
- flows are often not normally distributed;
- 3.
- downward biased flow predictions due to producing estimates for the logarithm of flows instead of actual flows;
- 4.
- zero flows are problematic since the logarithm of zero is undefined.
Therefore, the Poisson log-linear regression specification for the family of spatial interaction
models was proposed (Flowerdew, Aitkin 1982, Flowerdew, Lovett 1988). This specification
assumes that the number of flows between 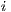 and
and 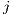 is drawn from a Poisson distribution
with mean,
is drawn from a Poisson distribution
with mean, 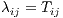 , where
, where 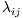 is assumed to be logarithmically linked to the linear
combination of variables,
is assumed to be logarithmically linked to the linear
combination of variables,
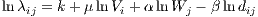 | (14) |
and exponentiating both sides of the equation yields the unconstrained Poisson log-linear gravity model,
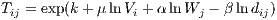 | (15) |
where equations (14) and (15) refer to the unconstrained model with a power function distance-decay. As previously mentioned, using fixed effects for the balancing factors in equations (4), (6), (8) and (9), the constrained variants of the family of spatial interaction models can be specified as,
where
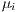 are origin fixed effects and
are origin fixed effects and 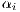 are destination fixed effects that achieve the same
results as including balancing factors (Tiefelsdorf, Boots 1995). Notice that k is the estimated
intercept and must be included in these log-linear models (equation 12–18) to ensure the total
number of flows is conserved, despite not being included in the maximum entropy models
where such conservation is implied. Similar to equation (13), the exponential function
distance-decay can be specified in equation (15, 16–18) by omitting the logarithm associated
with
are destination fixed effects that achieve the same
results as including balancing factors (Tiefelsdorf, Boots 1995). Notice that k is the estimated
intercept and must be included in these log-linear models (equation 12–18) to ensure the total
number of flows is conserved, despite not being included in the maximum entropy models
where such conservation is implied. Similar to equation (13), the exponential function
distance-decay can be specified in equation (15, 16–18) by omitting the logarithm associated
with 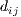 . Using Poisson regression is more representative of flows and satisfies
limitations (1) and (2) and it also alleviates limitations (3) and (5) since we no longer
need to take the logarithm of
. Using Poisson regression is more representative of flows and satisfies
limitations (1) and (2) and it also alleviates limitations (3) and (5) since we no longer
need to take the logarithm of 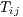 . Using fixed effects within Poisson regression to
calibrate the doubly-constrained model also avoids the need for iterative computation
of the balancing factors that exists in other calibration methods (Fotheringham,
O’Kelly 1989).
. Using fixed effects within Poisson regression to
calibrate the doubly-constrained model also avoids the need for iterative computation
of the balancing factors that exists in other calibration methods (Fotheringham,
O’Kelly 1989).
Calibration of Poisson regression can be carried out within a generalized linear modeling
framework (GLM) using iteratively weighted least squares (IWSL), which converges to the
maximum likelihood estimates for the parameter estimates (Nelder, Wedderburn 1972). To
maintain computational efficiency with increasingly larger spatial interaction datasets, SpInt is
built upon a custom GLM/IWLS routine that leverages sparse data structures for the
production-constrained, attraction-constrained, and doubly-constrained models. As the number
of locations in these models increases, so the does the number of binary indicator variables
needed to construct the fixed effects that enforce the constraints. Therefore, larger spatial
interaction datasets become increasingly sparse and the utilization of sparse data structures
takes advantage of this feature. As a metric, constrained models with 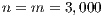 locations, which implies
locations, which implies 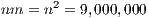 observed flows when each location is an
origin and destination, can be calibrated within minutes on a standard macbook pro
notebook.
observed flows when each location is an
origin and destination, can be calibrated within minutes on a standard macbook pro
notebook.
2.3 Model fit statistics
In order to evaluate the fit of spatial interaction models, it has been recommended that a
variety of statistics be used (Knudsen, Fotheringham 1986), which is the approach taken in
SpInt. For the log-normal regression specification, it is popular to utilize the coefficient of
determination (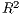 ), though this statistic is not available within the GLM framework used by
SpInt. In replacement of the
), though this statistic is not available within the GLM framework used by
SpInt. In replacement of the 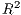 statistic, the SpInt framework provides a pseudo
statistic, the SpInt framework provides a pseudo 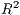 based
on the likelihood function (McFadden 1974),
based
on the likelihood function (McFadden 1974),
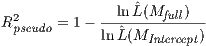 | (19) |
where 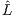 is the likelihood of an estimated model,
is the likelihood of an estimated model, 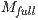 is the model including all
explanatory variables of interest, and
is the model including all
explanatory variables of interest, and 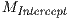 is the model with only an intercept (i.e., no
covariates). Like the
is the model with only an intercept (i.e., no
covariates). Like the 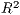 statistic, the pseudo version is at a maximum at a value of 1 with
higher values denoting better model fit. To account for model complexity, there is also an
adjusted version of this statistic,
statistic, the pseudo version is at a maximum at a value of 1 with
higher values denoting better model fit. To account for model complexity, there is also an
adjusted version of this statistic,
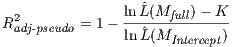 | (20) |
where 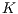 is the number of regressors. If model fit does not sufficiently improve, then it is
possible for this measure to decrease as variables are added, signaling that the additional
variables do not contribute towards a better model fit. Henceforth, these pseudo
is the number of regressors. If model fit does not sufficiently improve, then it is
possible for this measure to decrease as variables are added, signaling that the additional
variables do not contribute towards a better model fit. Henceforth, these pseudo 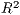 statistics
are referred to solely as
statistics
are referred to solely as 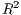 and adjusted
and adjusted 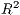 . Another model fit statistic available in the
SpInt module that also accounts for model complexity is the Akaike information criterion
(AIC),
. Another model fit statistic available in the
SpInt module that also accounts for model complexity is the Akaike information criterion
(AIC),
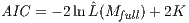 | (21) |
where lower AIC values indicate a better model fit (Akaike 1974). This statistic is grounded in information theory, whereby the AIC is an asymptotic estimate of the information that is lost by using the full model to represent a given theoretical process.
The 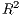 and AIC are designed for model selection, which means they should not be used
to compare between different spatial systems. One solution to this issue is the standardized
root mean square error (SRMSE),
and AIC are designed for model selection, which means they should not be used
to compare between different spatial systems. One solution to this issue is the standardized
root mean square error (SRMSE),
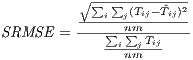 | (22) |
where the numerator is the root mean square error of the observed flows, 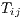 , and the flows
predicted by the model,
, and the flows
predicted by the model, 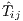 , and the denominator is the mean of the observed flows and is
responsible for standardization of the statistic. Here,
, and the denominator is the mean of the observed flows and is
responsible for standardization of the statistic. Here, 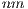 is the number of origin-destination
pairs that constitute the system of flows. A SRMSE value of 0 indicates perfect model fit, while
higher values indicate decreasing model fit; however, the upper limit of the statistic is not
necessarily 1 and will depend on the distribution of the observed values (Knudsen,
Fotheringham 1986).
is the number of origin-destination
pairs that constitute the system of flows. A SRMSE value of 0 indicates perfect model fit, while
higher values indicate decreasing model fit; however, the upper limit of the statistic is not
necessarily 1 and will depend on the distribution of the observed values (Knudsen,
Fotheringham 1986).
One final fit statistic, a modified Sorensen similarity index (SSI), is included within the SpInt module because it has become increasingly popular in some spatial interaction literature that deals with non-parametric models (Lenormand et al. 2012, Masucci et al. 2012, Yan et al. 2013). Using the same symbol definition from the SRMSE, the SSI is defined as,
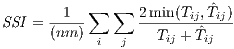 | (23) |
which is bounded between values of 0 and 1 with values closer to 1 indicating a better model fit.
3 An illustrative example: migration in Austria
3.1 The data
Despite being a small toy dataset, the following example is utilized for consistency since it was
previously used to demonstrate spatial interaction modeling in the R programming language
(Dennett 2012). The data are migration flows between Austrian NUTS level 2 regions in 2006.
In order to use a regression-based calibration, the data has to be transformed from
the matrices and vectors described in equations (1)–(9) to a table where each row
represents a single origin-destination dyad,  and any variables associated with
locations
and any variables associated with
locations  and
and 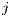 . Details on how to do this are outlined further in LeSage,
Pace (2008), though this has already been done in the example data. Let’s have a
look!
. Details on how to do this are outlined further in LeSage,
Pace (2008), though this has already been done in the example data. Let’s have a
look!
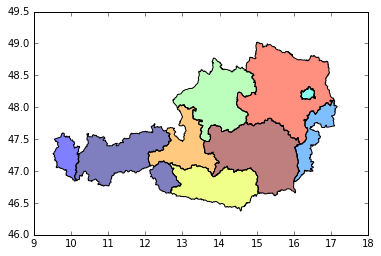
import geopandas as gp
%pylab inline
austria_shp = gp.read_file('austria.shp')
austria_shp.plot()
austria = pd.read_csv('austria.csv')
austria.head()
0 0 AT11 AT11 0 4016 5146 1.000000e-300
1 1 AT11 AT12 1131 4016 25741 1.030018e+02
2 2 AT11 AT13 1887 4016 26980 8.420467e+01
3 3 AT11 AT21 69 4016 4117 2.208119e+02
4 4 AT11 AT22 738 4016 8634 1.320075e+02
The Origin and Destination columns refer to the labels for origin locations, 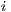 , and the
labels for destination locations,
, and the
labels for destination locations, 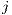 , the Data column is the number of flows between i and j,
the Oi and Dj columns are the number of total out-flows at i and total in-flows at j,
respectively, and the Dij column is the Euclidian distance between the centroids of
, the Data column is the number of flows between i and j,
the Oi and Dj columns are the number of total out-flows at i and total in-flows at j,
respectively, and the Dij column is the Euclidian distance between the centroids of
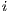 and
and 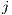 . In this case we use the total out-flow and total in-flow as variables to
describe how emissive an origin is and how attractive a destination is. If we want
a more informative and interesting model we can replace these with application
specific variables that pertain to different hypotheses. Next, lets format the data into
arrays.
. In this case we use the total out-flow and total in-flow as variables to
describe how emissive an origin is and how attractive a destination is. If we want
a more informative and interesting model we can replace these with application
specific variables that pertain to different hypotheses. Next, lets format the data into
arrays.
flows = austria['Data'].values
Oi = austria['Oi'].values
Dj = austria['Dj'].values
Dij = austria['Dij'].values
Origin = austria['Origin'].values
Destination = austria['Destination'].values
The Oi and Dj vectors need not be 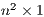 arrays. In fact, they can be
arrays. In fact, they can be 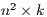 where
where
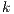 is the number of variables that are being used to describe either origin or destination
attributes associated with flows. It should also be noted that intra-zonal flows have been
excluded (the first line of code above). This is sometimes done because intra-zonal
flows are large compared to inter-zonal flows and would therefore heavily influence
the model or because it is not possible to adequately define a distance associated
with intra-zonal flows. Some solutions to these issues have been proposed (Kordi
et al. 2012, Tsutsumi, Tamesue 2011), though for simplicity, intra-zonal were removed for
this example.
is the number of variables that are being used to describe either origin or destination
attributes associated with flows. It should also be noted that intra-zonal flows have been
excluded (the first line of code above). This is sometimes done because intra-zonal
flows are large compared to inter-zonal flows and would therefore heavily influence
the model or because it is not possible to adequately define a distance associated
with intra-zonal flows. Some solutions to these issues have been proposed (Kordi
et al. 2012, Tsutsumi, Tamesue 2011), though for simplicity, intra-zonal were removed for
this example.
3.2 Calibrating the models
Now, lets load the main SpInt functionality and calibrate some models. The “family” of spatial interaction models are found within the gravity namespace of the SpInt module and the estimated parameters can be accessed via the params attribute of a successfully instantiated spatial interaction model.
from pysal.contrib.spint.gravity import Production
from pysal.contrib.spint.gravity import Attraction
from pysal.contrib.spint.gravity import Doubly
Unconstrained (basic gravity) model
Production-constrained model
Attraction-constrained model
Doubly-constrained model
Note that for the above examples the print statement for the constrained models params attribute is limited to print only the main model variables (i.e., not fixed effects), though it is still possible to access the fixed effect parameters too.
0.68945769 1.15434225 1.01013674 0.90285448 -0.0072617 ]
The first parameter is always the overall intercept with the subsequent 8 parameters
representing the fixed effects in this case. You might ask, “why not 9 fixed effects for the 9
different regions?”. Due to the coding scheme used in SpInt, and many popular statistical
programming languages, you would use 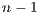 binary indicator variables in the design matrix
to include the fixed effects for all 9 regions in the model. While the non-zero entries in
these columns of the design matrix indicate which rows are associated with which
region, where a row has all zero entries then implicitly refers to the
binary indicator variables in the design matrix
to include the fixed effects for all 9 regions in the model. While the non-zero entries in
these columns of the design matrix indicate which rows are associated with which
region, where a row has all zero entries then implicitly refers to the 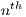 region
that has been left out. In SpInt, this is always the first origin or destination for the
production-constrained and attraction-constrained models. For the doubly-constrained model,
both the first origin and the first destination are left out (Tiefelsdorf, Boots 1995). In
terms of interpreting the parameters, these dropped locations are assumed to be
0.
region
that has been left out. In SpInt, this is always the first origin or destination for the
production-constrained and attraction-constrained models. For the doubly-constrained model,
both the first origin and the first destination are left out (Tiefelsdorf, Boots 1995). In
terms of interpreting the parameters, these dropped locations are assumed to be
0.
You can also access typical model diagnostics, such as standard errors (std_err), t-values (tvalues), p-values (pvalues), and confidence intervals (cont_int).
3.3 Interpreting the parameters
First, it will be demonstrated how to interpret the coefficients associated with the main model variables from a general Poisson regression. However, because the spatial interaction model is a log-linear Poisson regression (i.e., we take the log of the explanatory variables) the same interpretation often cannot be applied because we are working in logarithmic space. Therefore, it will also be demonstrated how to interpret the parameters when they are associated with a logged explanatory variable.
Recall from the previous section that the exponential distance-decay specification results in
a model that does not take the logarithm of 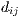 . Therefore, we can use an unconstrained
gravity model with an exponential distance-decay specification to demonstrate a typical
interpretation of coefficients from a Poisson regression.
. Therefore, we can use an unconstrained
gravity model with an exponential distance-decay specification to demonstrate a typical
interpretation of coefficients from a Poisson regression.
-6.22938370e-03 is the coefficient for the distance variable in the above example. In Poisson
regression, the coefficients are typically interpreted as the proportionate change in the
predicted response, here 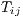 , if we increase an explanatory variable by 1 unit (Cameron,
Trivedi 2013). Technically, this is expressed as,
, if we increase an explanatory variable by 1 unit (Cameron,
Trivedi 2013). Technically, this is expressed as,
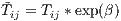 | (24) |
where 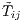 is the new value of
is the new value of 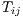 and
and 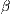 is a coefficient, here the one typically
associated with distance in a Poisson log-linear spatial interaction model with an
exponential function distance-decay. For this example, this means from a 1 unit increase
in distance, holding all other factors constant, if our model predicted 2,500 flows,
then we can expect the number of flows to decrease to approximately 2,484.475. We
can also identify the percent change expected from a one unit increase in distance
using,
is a coefficient, here the one typically
associated with distance in a Poisson log-linear spatial interaction model with an
exponential function distance-decay. For this example, this means from a 1 unit increase
in distance, holding all other factors constant, if our model predicted 2,500 flows,
then we can expect the number of flows to decrease to approximately 2,484.475. We
can also identify the percent change expected from a one unit increase in distance
using,
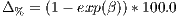 | (25) |
which serves as an alternative interpretation of 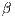 . In this case, we could say that from a 1
unit increase in distance we could expect the number of predicted flows to decrease by
approximately 0.621%.
. In this case, we could say that from a 1
unit increase in distance we could expect the number of predicted flows to decrease by
approximately 0.621%.
However, neither equation (24) nor (25) is applicable when the coefficient is associated with
a logged explanatory variable. This is important for Poisson log-linear spatial interaction
models because this applies to the origin and destination variables when using an exponential
function of distance-decay and to the origin, destination, and distance variables when
using a power function of distance-decay. In these cases, the interpretation of the
coefficients becomes the percent change in the predicted response, here 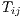 , if we
increase the associated explanatory variable by 1% (Cameron, Trivedi 2013). For
example, 8.91445153e-01 is the coefficient associated with destination total in-flows (i.e.,
attractiveness) in the above example. Then if we increase the in-flows to location
, if we
increase the associated explanatory variable by 1% (Cameron, Trivedi 2013). For
example, 8.91445153e-01 is the coefficient associated with destination total in-flows (i.e.,
attractiveness) in the above example. Then if we increase the in-flows to location 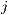 by
1%, say from
by
1%, say from 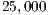 to
to 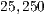 , and holding all other factors constant, we can
expect the number of flows from
, and holding all other factors constant, we can
expect the number of flows from 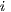 to
to 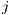 (i.e.,
(i.e., 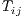 ) to increase from
) to increase from 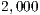 to
to
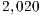 3.
3.
Finally, the fixed effects in the constrained models can be interpreted such that the mean
predicted flows, 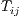 , are
, are 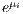 (
(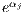 ) times larger if they originate (terminate) from location
) times larger if they originate (terminate) from location
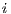 (location
(location 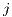 ) (Cameron, Trivedi 2013), where
) (Cameron, Trivedi 2013), where 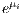 is equivalent notation for
is equivalent notation for
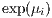 .
.
3.4 Assessing model fit
We can compare the different model fit statistics across the four types of spatial interaction models for this example. Let’s process the statistics into a tidy table and have a look.
model_name = ['grav', 'prod', 'att', 'doub']
col_names = ['R2', 'adjR2', 'AIC', 'SRMSE', 'SSI']
models = [gravity, production, attraction, doubly]
for model in models:
R2.append(model.pseudoR2)
adjR2.append(model.adj_pseudoR2)
SSI.append(model.SSI)
SRMSE.append(model.SRMSE)
AIC.append(model.AIC)
cols = {'model_name': model_name,
'R2': R2,
'adjR2': adjR2,
'SSI': SSI,
'SRMSE': SRMSE,
'AIC': AIC }
data = pd.DataFrame(cols).set_index('model_name')
data[col_names]
model_name
grav 0.885764 0.885718 20122.074349 0.607776 0.727358
prod 0.910156 0.910031 15841.253799 0.464520 0.740914
att 0.909355 0.909230 15982.313101 0.584048 0.752155
doub 0.943540 0.943335 9977.159141 0.379286 0.811852
From this table we can see that all of the fit statistics indicate a better model fit as
constraints are introduced. That is, the weakest model fit is consistently related to the
gravity model, with similarly increased model fit for the production-constrained and
attraction-constrained models, and finally, the best model fit is associated with the doubly
constrained model. We can also see that the 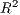 and adjusted
and adjusted 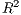 are very close, since these
models have a very similar number of explanatory variables, thereby resulting in little or no
penalization for model complexity.
are very close, since these
models have a very similar number of explanatory variables, thereby resulting in little or no
penalization for model complexity.
We can also take a look at whether the power or exponential distance-decay specification results in a better model fit. For simplicity, lets just take a look at the SRMSE for a doubly constrained model.
pow_doubly = Doubly(flows, Origin, Destination, Dij, 'pow')
print 'SRMSE for exp distance-decay: ', pow_doubly.SRMSE
For this example, it looks like the power distance-decay specification results in a better model fit.
3.5 Local models
The SpInt module also makes it possible to calibrate “local” models, which subset the data by specific origins or destinations in order to investigate how spatial interaction processes vary over space (Fotheringham, Brunsdon 1999). Below is an example of how to get local parameters and local diagnostics for a gravity model subset by its origins. The result is a dictionary of lists where the keys are the different sets of local values including parameters, hypothesis testing diagnostics, and the previously reviewed fit statistics.
local_gravity = gravity.local(Origin, np.unique(Origin))
Lets take a look at the local distance-decay parameters. The origin, destination and
distance-decay parameters are indexed sequentially through the design matrix starting with 0
as you move through the origin attributes, through to the destination attributes, and finally
the distance-decay attribute. Therefore, for 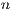 variables, the distance-decay parameters are
always the n - 1th parameter, in this case of 3 variables: param2.
variables, the distance-decay parameters are
always the n - 1th parameter, in this case of 3 variables: param2.
We can also take a look at the local 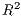 .
.
Both the local distance-decay and the 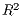 show some variation. We can explore this spatially,
by mapping the local values. First, lets join the local values to a shapefile and then plot the
local distance-decay parameters
show some variation. We can explore this spatially,
by mapping the local values. First, lets join the local values to a shapefile and then plot the
local distance-decay parameters
local_vals = pd.DataFrame({'betas': local_gravity['param2'],
'Dest':np.unique(Origin),
'pseudoR2': local_gravity['pseudoR2']})
local_vals = pd.merge(local_vals, austria_shp[['NUTS_ID', 'geometry']],
left_on='Dest', right_on='NUTS_ID')
local_vals = gp.GeoDataFrame(local_vals)
#Plot betas - use inverse so the most negative values are "higher"
fig = plt.figure()
ax = fig.add_subplot(111)
local_vals['inv_betas'] = (local_vals['betas']*-1)
local_vals.plot('inv_betas', cmap='Blues', ax=ax)
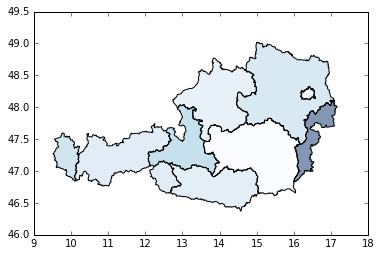
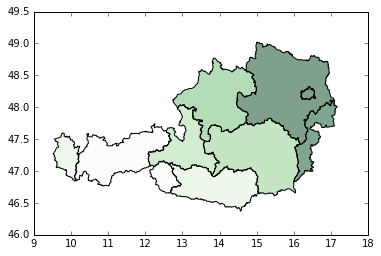
Next, lets map the local  values. Above we can see a much stronger distance-decay for
the most westerly region. Below we can see that the model fit is stronger in the north-west and
decreases in the south-east. Using these patterns, we could then further postulate why they
arise or how we might be able to improve model fit.
values. Above we can see a much stronger distance-decay for
the most westerly region. Below we can see that the model fit is stronger in the north-west and
decreases in the south-east. Using these patterns, we could then further postulate why they
arise or how we might be able to improve model fit.
ax = fig.add_subplot(111)
local_vals.plot('pseudoR2', cmap='Greens', ax=ax)
4 Further functionality
In addition to all of the features presented here, there are several other tools that exist in SpInt or could be added. First, there are dispersion tests available in the dispersion namespace of the SpInt module, which can be used to test whether or not the Poisson equidispersion assumption is met. That is, that the conditional mean and variance are equivalent, which can be unrealistic in many scenarios. If these tests indicate overdispersion or underdispersion, then it might be appropriate to use a Quasi-Poisson model, which relaxes the equidispersion assumption of the Poisson model. The resulting parameter estimates are equivalent to the Poisson model, but the standard errors are typically larger whenever equidispersion does not hold (Wedderburn 1974). The Quasi-Poisson model specification can be carried out by setting Quasi=True in any of the spatial interaction models introduced here. Alternatively, it might be more appropriate to change the underlying probability model from Poisson to that of negative binomial or a zero-inflated model. However, this has not yet been implemented in SpInt and therefore remains as future work.
Another area of potential expansion is to accommodate several paradigms for incorporating spatial effects into spatial interaction models, such as competing destinations (Fotheringham 1983), a spatial lag autoregressive model (LeSage, Pace 2008), or an eigenvector spatial filter model (Chun 2008). These paradigms require code that computes additional variables, more complex calibration techniques, and specialized representations of spatial relationships. Some solutions to the latter are available in the spintW namespace of the weights module of PySAL. While there is still much work to be done to develop a more robust set of open source spatial interaction modeling tools, SpInt provides a starting point for which to build upon.
References
Akaike H (1974) A new look at the statistical model identification. Automatic Control, IEEE Transactions on 19: 716–723. CrossRef.
Cameron AC, Trivedi PK (2013) Regression Analysis of Count Data. Cambridge University Press, New York. CrossRef.
Chun Y (2008) Modeling network autocorrelation within migration flows by eigenvector spatial filtering. Journal of Geographical Systems 10: 317–344. CrossRef.
Dennett A (2012) Estimating flows between geographical locations:‘get me started in’spatial interaction modelling. Working Paper 184, Citeseer, UCL
Flowerdew R, Aitkin M (1982) A Method of Fitting the Gravity Model Based on the Poisson Distribution. Journal of Regional Science 22: 191–202. CrossRef.
Flowerdew R, Lovett A (1988) Fitting Constrained Poisson Regression Models to Interurban Migration Flows. Geographical Analysis 20: 297–307. CrossRef.
Fotheringham AS (1983) A new set of spatial-interaction models: the theory of competing destinations. Environment and Planning A 15: 15–36. CrossRef.
Fotheringham AS, Brunsdon C (1999) Local Forms of Spatial Analysis. Geographical Analysis 31: 340–358. CrossRef.
Fotheringham AS, O’Kelly ME (1989) Spatial Interaction Models:Formulations and Applications. Kluwer Academic Publishers, London
Knudsen D, Fotheringham A (1986) Matrix comparison, Goodness-of-fit, and spatial interaction modeling. International Regional Science Review 10: 127–147. CrossRef.
Kordi M, Kaiser C, Fotheringham AS (2012) A possible solution for the centroid-to-centroid and intra-zonal trip length problems. International Conference on Geographic Information Science, Avignon
Lenormand M, Huet S, Gargiulo F, Deffuant G (2012) A Universal Model of Commuting Networks. PLoS ONE 7: e45985. CrossRef.
LeSage JP, Pace RK (2008) Spatial Econometric Modeling Of Origin-Destination Flows. Journal of Regional Science 48: 941–967. CrossRef.
Masucci AP, Serras J, Johansson A, Batty M (2012) Gravity vs radiation model: on the importance of scale and heterogeneity in commuting flows. arXiv:1206.5735 [physics]. CrossRef.
McFadden D (1974) Conditional logit analysis of qualitative choice behavior. In: Zarembka P (ed), Frontiers in Econometrics. Academic Press, New York, 105–142
Nelder JA, Wedderburn RWM (1972) Generalized Linear Models. Journal of the Royal Statistical Society. Series A (General) 135: 370–384. CrossRef.
Tiefelsdorf M, Boots B (1995) The specification of constrained interaction models using the SPSS loglinear procedure. Geographical Systems 2: 21–38
Tsutsumi M, Tamesue K (2011) Intraregional Flow Problem in Spatial Econometric Model for Origin-destination Flows. Procedia - Social and Behavioral Sciences 21: 184–192. CrossRef.
Wedderburn RWM (1974) Quasi-Likelihood Functions, Generalized Linear Models, and the Gauss-Newton Method. Biometrika 61: 439–447. CrossRef.
Wilson AG (1971) A family of spatial interaction models, and associated developments. Environment and Planning A 3: 1–32. CrossRef.
Yan XY, Zhao C, Fan Y, Di Z, Wang WX (2013) Universal Predictability of Mobility Patterns in Cities. arXiv:1307.7502 [physics]. CrossRef.