Volume
4, Number 3, 2017, 77–86 journal homepage:
region.ersa.org
Volume
4, Number 3, 2017, 77–86 journal homepage:
region.ersa.orgDOI: 10.18335/region.v4i3.169
Urban Concentration and Spatial Allocation of Rents from natural resources. A Zipf’s Curve Approach
1 University of Azores, Azores, Portugal Received: 17 October 2016/Accepted: 18 May 2017Abstract. This paper aims at demonstrating how countries’ dependency on natural resources plays a crucial role in urban concentration. The Zipf curve elasticity is estimated for a group of countries and related to a set of indicators of unilateral transferences. Results show that in comparison to others, countries with higher urban concentration explained by higher Zipf curve elasticity have a higher percentage of income coming from natural resources and education expenditures whereas public spending in health and net outflow of foreign direct investment seem to have spatial redistribution effects. Summing up, there are signs that the spatial allocation of property rights over natural resources and related rents influences urban concentration.
Key words: Urban concentration; Zipf Curve; Natural Resources; Rents
1 Introduction
Globally, more people live in urban areas than in rural areas and the world’s fastest growing cities are located in Africa and Asia (United Nations 2014), these being increasingly connected to the complex constellation of the “New Urban World” (Kourtit, Nijkamp 2013). Notwithstanding this, urban concentration in the developing world is not necessarily a good thing and neither is it unmanageable. On the one hand, urban concentration can generate congestion, environmental disturbances and social problems that are difficult to address with reduced resources. On the other hand, urban concentration does not happen only due to global and undifferentiated factors, but may relate to manageable causes such as unilateral transferences between regions.
The ‘New Urban World’ is certainly interacting through competition, collaboration, exploitation and help. Actually, unilateral transferences between regions can occur when the rents from natural resources, distributed across the territory, go to the regions and places where their owners receive them. Permanent governmental transferences happen when taxes collected across the territory go to capital cities and to border areas where public services tend to be relatively more concentrated. Migrant remittances persist throughout time between immigrant places and emigrant localities. This is part of the migrant strategy that transfers a portion of their income to the areas where their families live. Finally, investment flows may lead also to spatial distribution of income. All of these unilateral and quite enduring transferences create persistent multiplier effects that accumulate in an uneven concentration of production and expenditure, employment and population, tradable and non-tradable activities.
Unilateral transferences between regions and the multiplier income effects associated with them explain why the spatial distribution of production may not be the same as the spatial distribution of expenditure. Therefore, it is not accurate to look at local and regional development and to the concomitant effects of urban concentration and rural desertification without taking into account unilateral transferences between places and regions.
In fact, the spatial allocation of rents of natural resources depends on the spatial distribution of property rights over natural resources and not on the territorial distribution of those resources. Due to the spatial distribution of property rights and the distribution of territorial resources being different, it is quite likely that permanent unilateral transferences occur and that dependent and exploited regions are created and maintained. Dependent regions are those, usually in the centre or at the territorial borders, who receive permanent transferences to obtain and secure the rents of territorial property rights. Exploited regions are those deprived from the rents of their territory (Dentinho 2012, 2017). The isolated estate of Von Thünen (1826) is a crucial reference if one wants to understand this, given that the author highlighted the creation of land rents, leaving the rent distribution implicit in the model. In the Von Thünen model, land rents go from territorial managers located in peripheral rings to the land owners located in the city centre; there the received rents generate income multiplier effects as thought by François Quesnay (1758). In the end, land ownership and rent distribution constitute crucial elements for urban concentration, regional development and, with free migration.
In extreme cases, one whole country can be concentrated into just one major city receiving the rents from a territory with much smaller localities. But in theory and in reality the hierarchy of cities is quite resilient as it is showed by Gibrat’s Law (1931) and by the Zipf law (1949), which states that the second largest city is half the size of the biggest, the third largest city is a third the size of the biggest, and so on. As said by Gabaix (1999) this means that the probability of the size of a city being greater than some limit S is proportional to 1∕S: P (size> S)= C∕Sμ; where μ = 1 and C = Constant.
There are many applications of Zipf’s estimates focusing on the population of cities, dimension of companies, webpage popularity, impact of tornados and earthquakes as well as a few other phenomena (Pinto et al. 2012). In an application to the Chinese cities (Anderson, Ying 2005) it is concluded that cities tend to stay in the same position in the ranking and that the lognormal distribution explains the ranking profile better than the Pareto distribution. Jiang et al. (2015) tested the stability of the Pareto coefficient for truncated series of cities in China. Black, Henderson (2003) work on United States Cities found out that there is a concentration in service cities. Bosker et al. (2008) looked at the evolution of German cities from 1925 until 1999 and proved that, besides the enormous shocks caused by the economic crises of the thirties, world war II, the cold war and the fall of the Berlin Wall, there are increasing returns on scale for city growth. In an application to South Africa (Morudu 2016) it was suggested that the Zipf curve could be used to estimate the population of cities for a determined year where census data is not available.
It is also common to find in the literature theoretical analysis of the Zipf curve. Cristelli et al. (2012) demonstrate that truncated series of city population influences the estimates of Zipf coefficients. Along with the work of Anderson, Ying (2005), Benguigui, Blumenfeld-Lieberthal (2007) argue that the Zipf curve can be concave, linear or convex depending on the country. Peng (2010)Peng (2010) proves that the shape of the Zipf curve relates to the development of the network of cities in China. Cordoba (2008) shows that the profile of the Zipf curve comes from the regularity of the growth process across cities. Many authors test the validity of different distributions to explain the population size of the cities (Loannides, Overman 2003, Nitsch 2005, Newman 2005, Giesen et al. 2010, Gómez-Déniz et al. 2014, Gómez-Déniz, Calderín-Ojeda 2015, Shujuan 2016, Luckstead, Devadoss 2017).
Finally, there are many attempts to explain the regularity of the hierarchy of cities. Ades, Glaeser (1995) found that political factors do influence urban concentration and that dictatorships occur in central cities that are, on average, 50% larger than democratic countries of similar size. Krugman (1996) suggests that nature is also hierarchical in river basins and that cities rooted in natural capital have also a string hierarchy. Eaton, Eckstein (1997) relate the hierarchy to intercity migration. Gabaix (1999) connects the Zipf law with relative city growth and points out that parameter μ = 1 does not change much with the age of the city network. Axtell, Florida (2001) reconcile the tension between centripetal and centrifugal forces. Duranton (2002) links the city hierarchy with a set of indicators related to innovation. Córdoba (2003) shows that the Zipf law happens when there is a similar growth path between cities. Giesen, Suedekum (2014) find that older cities tend to be larger than new ones. There is interesting literature linking urban concentration to economic growth (Bertinelli, Strobl 2007) where there is an optimal level of urban concentration that can be influenced by policy makers (Henderson 2003, Brülhart, Sbergami 2009). Kourtit, Nijkamp (2013) report that recently major cities, beyond being the engine for growth, show a rapid population rise while smaller ones shrink and can even fall below a critical sustainable population level. To my knowledge, there is not an analysis relating urban concentration to the distribution of rents from natural resources and other unilateral transfers although they very much reveal the institutional context of the territory that Ades, Glaeser (1995) tried to relate to the hierarchy of cities.
The aim of this paper is to look into urban concentration to test the hypothesis that the spatial allocation of rents from natural resources and other unilateral transferences do have a role in urban concentration. Section 2 presents the estimates of the Zipf elasticity for various countries. Section 3 links the estimated elasticity with the features of those countries and to unilateral transferences. Finally in Section 4 the discussion is based on the relation between spatial allocation of property rights and urban concentration.
2 Zipf’s Law and the level of Urban Concentration
(a) Europe and North America
(b) Asia and Oceania
(c) Africa and South America
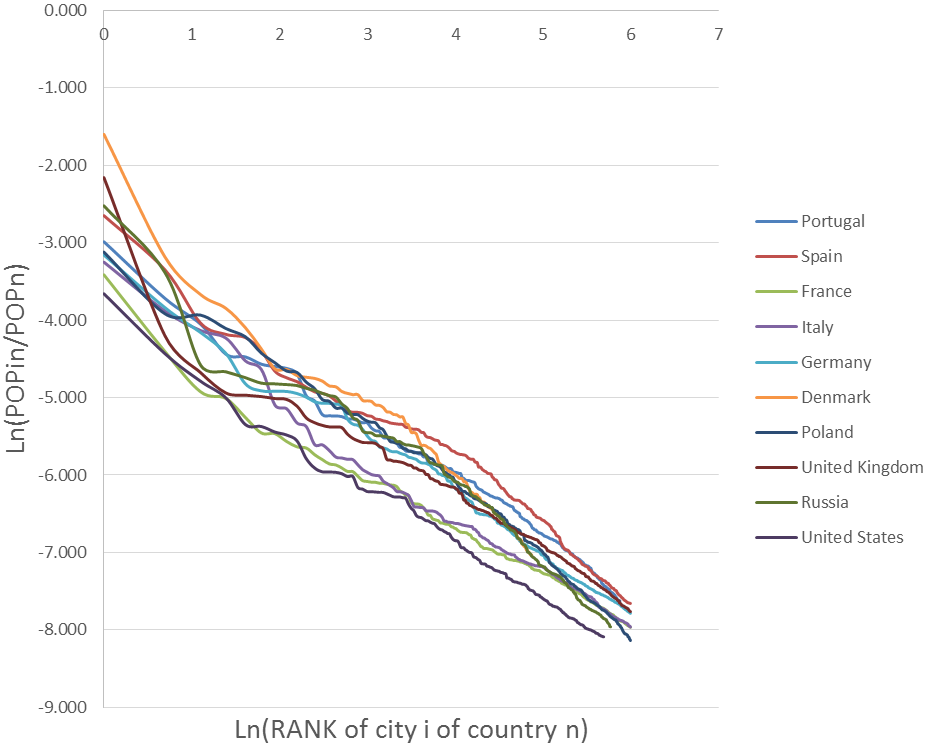
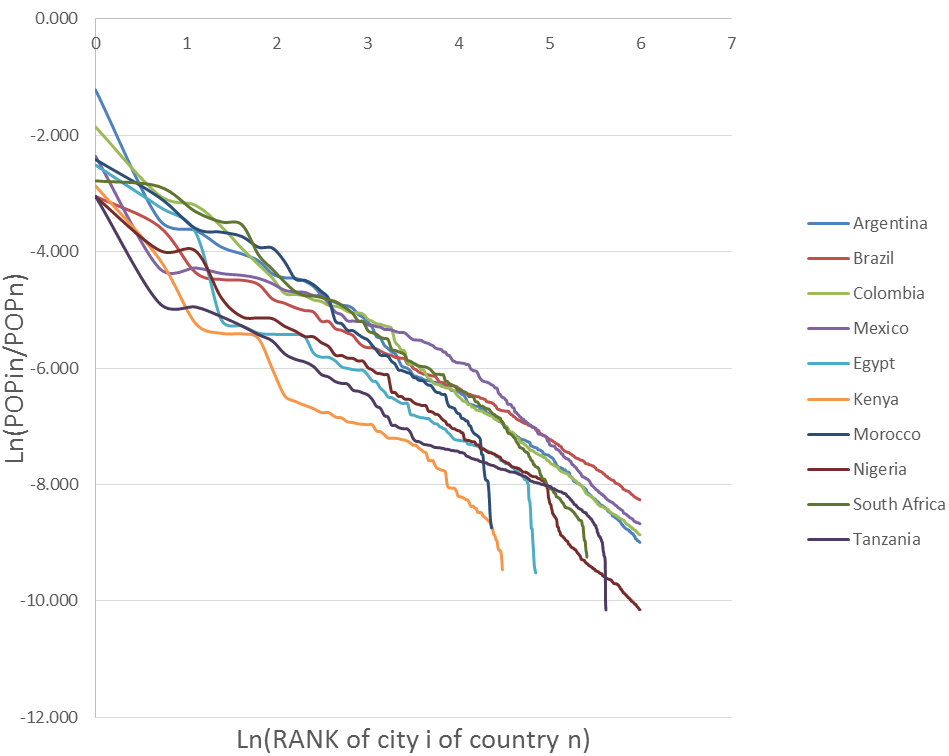
Data of city population by country was obtained from the site http://worldpopulationreview.com/countries/. The population of each city (Popi) was divided by the total population of the country (Pop) obtaining the weight of each city in the total population of the country. Then the coefficient of the Zipf curves by Country (μ) (Figure 1) was estimated regressing the logarithm of the weight of the city population with the logarithm of the rank order of the city (Equation 1).
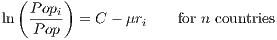 | (1) |
The Zipf curves for European and North American countries show, with the exception of Russia, lower slopes than in other parts of the world. Nevertheless, there are countries, like the United Kingdom or Denmark, where the major city reduces the importance of the following ones. In other countries, a set of major cities reduces the weight of those who are next in the hierarchy, this being the case of Russia and Spain. Finally, the middle part of the curves do not show a very monotonous profile, which may indicate the existence of unilateral transferences also involving middle ranked cities, with this appearing to be more relevant in the United States and Italy. The Zipf curves for Asian and Oceania countries show tails in the distribution of cities indicating that parts of the countries are very depopulated due to mountain areas (Pakistan and Nepal), ocean archipelagos (Japan and Indonesia) or by long lasting conflicts (Sri Lanka). On the other hand, research rich countries have higher concentrations of their resource rents in major cities (Saudi Arabia, Kazakhstan). The Zipf curves for Africa and South American countries also show tails associated to remote areas, mainly in African countries (Kenya, Morocco, Egypt, Nigeria, South Africa and Tanzania), and also in countries from South America (Argentina, Brazil, Colombia and Mexico) with a larger concentration of population in major towns.
 (a) Europe and North America
(a) Europe and North America
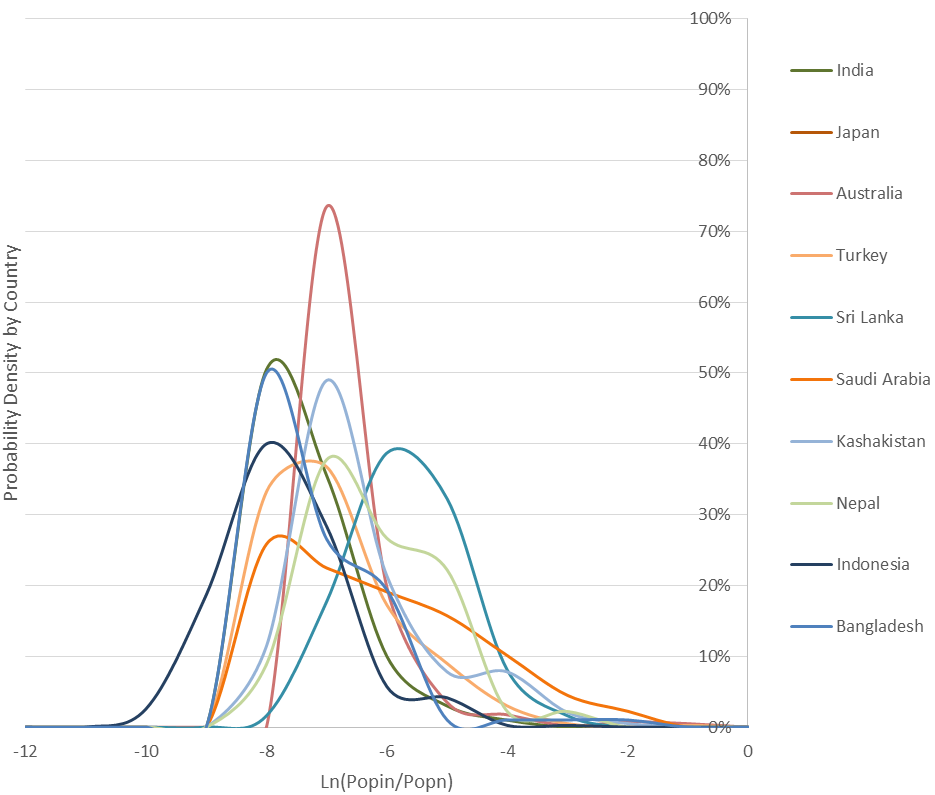 (b) Asia and Oceania
(b) Asia and Oceania
 (c) Africa and South America
(c) Africa and South America
Figure 2 shows the kernel densities of the logarithm of the relative size of the cities by country. Looking closer it is possible to identify various groups of countries. The countries in Europe and North America present very similar Pareto type distributions with more cities in the lower ranks of the distribution. For smaller countries close to bigger ones, like Denmark and somehow Portugal, there is a shift to smaller cities in the distribution. The distributions for countries in Asia, Oceania, Africa and South America are quite different from each other. Some Asian countries like India, Bangladesh and Australia behave like European and North American countries. A second group of countries do not have a mode in the cities with lower size; this happens with countries that have some remote and small cities like Brazil, the United States, Japan, Morocco, South Africa, Tanzania, Sri Lanka, Kazakhstan, Pakistan, Nepal, Poland and Indonesia. Finally, there are countries with two modes in the distribution of city sizes showing that the first cities emptied the second ones; this is the case of Nigeria, Turkey, Egypt, Kenya, Colombia, Mexico and Argentina.
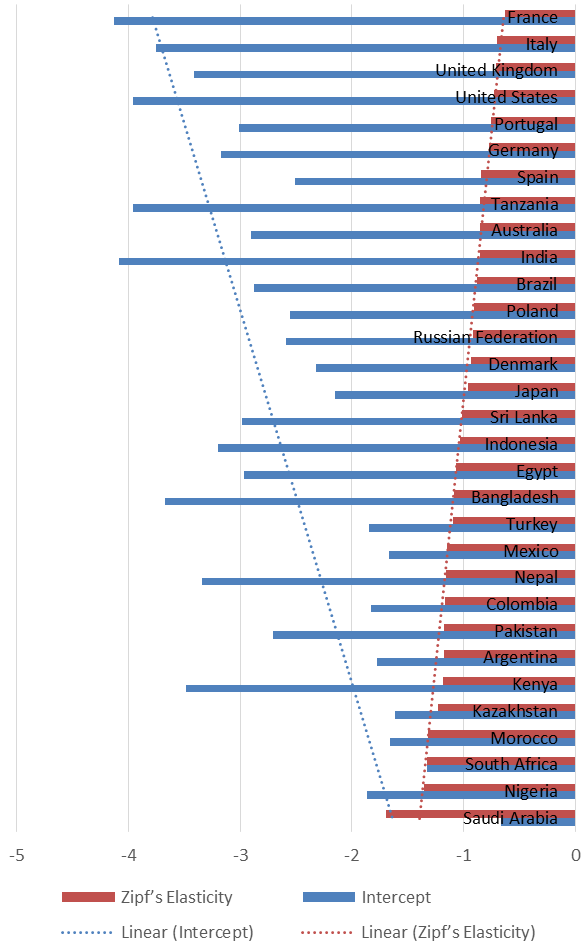
The estimates of the Zipf curves by country are presented in Figure 3. As expected the intercept (C) increases when the Zipf coefficient (μ) decreases. Countries that do not match this expectable rule are the ones that have a reduced sample of cities: Tanzania, India, Bangladesh, Nepal, Kenya and Saudi Arabia.
Results in Figure 2 show that, although the value expected for the Zipf coefficient in the literature (μ = 1) is the average estimate, there are quite significant differences between more concentrated countries like Saudi Arabia (μ = -1.698) and more decentralized countries such as France (μ = -0.634).
If people can migrate from less affluent to more affluent places, the expected value of the Zipf elasticity is around 1, as proved by (Gabaix 1999). For values of the Zipf elasticity higher than 1 there is a concentration of the population in the bigger cities whereas for values lower than that threshold there is a distribution of the population in the smaller cities. This paper attempts to find out if the spatial allocation of rents from natural resources and from other unilateral regional transferences (private and public) has a role in the urban concentration profile represented by the Zipf coefficient.
3 Zipf’s Law and the level of Urban Concentration
To answer this question the positive value of the Zipf elasticity for each country is regressed against different variables that relate to unilateral income transferences (Data in Table 1):
- 1.
- The Total natural resources rents as a percentage of gross national income;
- 2.
- Public heath expenditure as a percentage of gross national income.
- 3.
- Adjusted savings: education expenditure as a percentage of gross national income.
- 4.
- Net outflows of foreign direct investment as a percentage of gross national income;
- 5.
- Workers remittances also as a percentage of gross national income;
| Country name | Num- | Intercept | Zipf’s | Total | Public | Adjusted | FDI, | Workers’ |
| ber | elasti- | natural | health | savings: | net | remit- | ||
| of | city | resour- | expen- | Education | out- | tances1 | ||
| cities | ces | diture1 | expen- | flows1 | ||||
| rents1 | diture1 | |||||||
| Saudi Arabia | 89 | -0.671*** | -1.698*** | 53.73 | 2.7 | 7.186 | 0.867 | 0.05 |
| Nigeria | 400 | -1.868*** | -1.352*** | 32.56 | 1.92 | 0.850 | 0.465 | 5.1 |
| South Africa | 223 | -1.327*** | -1.326*** | 4.62 | 3.94 | 5.434 | -0.044 | 0.31 |
| Morocco | 78 | -1.661*** | -1.317*** | 2.61 | 1.97 | 5.201 | 0.639 | 7.07 |
| Kazakhstan | 192 | -1.614*** | -1.230*** | 27.60 | 2.55 | 4.413 | 5.294 | 0.2 |
| Kenya | 88 | -3.482*** | -1.182*** | 1.33 | 2.11 | 5.916 | 0.005 | 5.52 |
| Argentina | 400 | -1.778*** | -1.178*** | 6.07 | 4.42 | 6.010 | 0.262 | 0.17 |
| Pakistan | 400 | -2.703*** | -1.173*** | 3.92 | 0.84 | 1.565 | 0.027 | 5.48 |
| Colombia | 400 | -1.833*** | -1.165*** | 7.86 | 5.52 | 3.907 | 2.272 | 1.41 |
| Nepal | 45 | -3.341*** | -1.162*** | 3.39 | 1.83 | 4.202 | 0.000 | 21.66 |
| Mexico | 400 | -1.664*** | -1.147*** | 7.29 | 3.09 | 4.798 | 1.310 | 2.13 |
| Turkey | 400 | -1.846*** | -1.099*** | 0.45 | 5.07 | 2.644 | 0.200 | 0.12 |
| Bangladesh | 98 | -3.673*** | -1.089*** | 3.28 | 1.17 | 1.811 | 0.000 | 10.81 |
| Egypt | 127 | -2.968*** | -1.073*** | 10.13 | 1.74 | 4.411 | 0.537 | 3.53 |
| Indonesia | 385 | -3.202*** | -1.037*** | 5.95 | 1.28 | 4.328 | 0.376 | 0.98 |
| Sri Lanka | 62 | -2.984*** | -1.017*** | 0.50 | 1.32 | 1.744 | 0.086 | 8.38 |
| Japan | 514 | -2.149*** | -0.962*** | 0.03 | 7.83 | 3.185 | 1043 | 0.03 |
| Denmark | 130 | -2.317*** | -0.937*** | 2.13 | 9.71 | 7.278 | 1.06 | 0.2 |
| Russian Fed. | 319 | -2.591*** | -0.914*** | 19.90 | 3.15 | 3.544 | 3.531 | 0.35 |
| Poland | 400 | -2.557*** | -0.907*** | 0.98 | 5.42 | 4.869 | 1.177 | 1.62 |
| Brazil | 400 | -2.876*** | -0.882*** | 5.30 | 4.24 | 5.162 | 0.541 | 0.19 |
| India | 200 | -4.086*** | -0.857*** | 4.04 | 1.18 | 3.082 | 0.781 | 3.21 |
| Australia | 400 | -2.900*** | -0.852*** | 8.31 | 5.93 | 4.536 | 2.167 | 0.43 |
| Tanzania | 275 | -3.956*** | -0.852*** | 6.78 | 4.05 | 2.393 | 0.000 | 0.11 |
| Spain | 400 | -2.513*** | -0.842*** | 0.06 | 6.95 | 4.210 | 2.710 | 0.76 |
| Germany | 400 | -3.175*** | -0.771*** | 0.12 | 8.97 | 4.394 | 3.392 | 0.35 |
| Portugal | 355 | -3.013*** | -0.759*** | 0.33 | 7.50 | 4.937 | -3.211 | 1.56 |
| USA | 295 | -3.954*** | -0.730*** | 1.00 | 9.49 | 4.789 | 2.432 | 0.04 |
| UK | 400 | -3.413*** | -0.712*** | 1.49 | 8.08 | 5.054 | 1.320 | 0.33 |
| Italy | 400 | -3.755*** | -0.699*** | 0.17 | 7.4 | 4.411 | 1.595 | 0.33 |
| France | 400 | -4.127*** | -0.634*** | 0.07 | 9.25 | 5.053 | 3.311 | 0.61 |
The gross national income per capita was included in the model and provided significant results as indicated by Pinto et al. (2012). Nevertheless, there were problems of colinearity with the public health expenditure and it is more informative for the present exercise to relate urban concentration with the spatial distribution of public spending than with the income level of the country. Table 2 presents the correlation between dependent and independent variables that indicates the strong positive correlation between the Zipf elasticity and the total natural resources rents and the strong negative correlation between the Zipf elasticity and the public health expenditures also slightly correlated with Workers’ remittances.
| Zipf’s | Total | Public | Adjusted | FDI, | Workers’ | |
| elasti- | natural | health | savings: | net | remit- | |
| city | resour- | expen- | Education | out- | tances | |
| ces | diture | expen- | flows | |||
| rents | diture2 | |||||
| Zipf’s elasticity | 1.00 | -0.65 | 0.64 | -0.05 | 0.18 | -0.26 |
| Total natural resources rents | -0.65 | 1.00 | -0.35 | 0.08 | 0.19 | -0.10 |
| Public health expenditure | 0.64 | -0.35 | 1.00 | 0.38 | 0.28 | -0.51 |
| Adjusted savings: Education | -0.05 | 0.08 | 0.38 | 1.00 | 0.10 | -0.30 |
| expenditure (% of GNI) | ||||||
| FDI, net outflows | 0.18 | 0.19 | 0.28 | 0.10 | 1.00 | -0.32 |
| Workers’ remittances | -0.26 | -0.10 | -0.51 | -0.30 | -0.32 | 1.00 |
Table 3 presents the estimated parameters of linear models that relate the urban concentration by country assessed by the Zipf elasticity with a set of unilateral transferences by country. Results are quite interesting:
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5
| ||||||
| Coef. | Sig. | Coef. | Sig. | Coef. | Sig. | Coef. | Sig. | Coef. | Sig. | |
| Adj R2 | 0.406 | 0.591 | 0.628 | 0.634 | 0.629 | |||||
| F | 21.51 | 22.67 | 17.88 | 14.02 | 11.19 | |||||
| Intercept | 0.923 | 0.000 | 1.121 | 0.000 | 1.014 | 0.000 | 1.017 | 0.000 | 0.967 | 0.000 |
| Total natural | 0.013 | 0.000 | 0.010 | 0.001 | 0.009 | 0.002 | 0.010 | 0.001 | 0.010 | 0.001 |
| resources rents3 | ||||||||||
| Public Health | -0.038 | 0.001 | -0.048 | 0.000 | -0.042 | 0.001 | -0.037 | 0.010 | ||
| expenditure3 | ||||||||||
| Adjusted savings: | 0.037 | 0.062 | 0.035 | 0.079 | 0.036 | 0.074 | ||||
| Education expenditure3 | ||||||||||
| FDI net outflows3 | -0.023 | 0.234 | -0.021 | 0.280 | ||||||
| Workers’ remittances3 | 0.008 | 0.428 | ||||||||
First, the Percentage on the GNI of the Total Natural Resource Rents has a positive, significant and consistent relation with the Zipf city elasticity by country. Each percent point of the Total natural resources rents on the GDP increases the Zipf city elasticity by around 0.010. In other words, assuming that natural resources are distributed across the territory, bigger cities seem to own the property rights over natural resources across the territory and, through the multiplier effects of those rents, it increases their weight in the country population. That is why countries like Saudi Arabia, Nigeria and Kazakhstan – with higher percentage of the rents of natural resources on the total GNI – attract more population to the bigger city.
Second, the percentage of public health expenditure in the gross national income has a spatial distributive effect that is consistent across the various regressions with a quite robust coefficient that varies around 0.038. Interestingly the percentage of the “Adjusted savings: Education expenditure” in the gross national income has an urban concentration effect of the same scale on the distributive effect of public health spending.
Third, although not significant, countries that are net exporters of foreign direct investment tend to have less urban concentration, indicating somehow that investment that goes outside goes also inside the country.
Finally, the Percentage on the GNI of the Workers Remittances has no robust effect in the urban concentration of the country. Furthermore as shown in Table 2, this is very much correlated with public health expenditures limiting the capacity of the results of Model 5. The attempt was to know if there was an indication that migrants in other countries tend either to secure population in smaller cities by sending remittances to their families that reside in those areas, or to invest their savings in more urbanized areas. A more profound analysis of differences between countries could be analyzed.
4 Discussion
The hypothesis tested in this exercise is quite simple: the spatial allocation of property rights over territorial resources has strong effects on the spatial profile of the urban network through the multiplier effects of income associated with rents from natural resources that goes from the places where those resources are located to the places of residence of their owners. The test relates the urban concentration of each country, assessed by the elasticity of the respective Zipf curve, with the percentage of income coming from the rents of natural resources.
Results confirm what Ades, Glaeser (1995) said: Institutions, namely those created by the spatial distribution of property rights over natural resources and by the geographical allocation of public spending, do have a role in the urban concentration throughout space. Furthermore, since huge amounts of rents from natural resources come from land, it is obvious, also from the research presented in this essay, that the main driver of major cities is Real Estate as justified by Castells (2012). To some extend we confirm the old intuition of the Von Thünen model that assumed that land rents go from territorial managers located in peripheral rings to the landowners located in the city centre where rents generate income multiplier effects as envisaged by Quesnay (1758). Regarding the Duranton (2002) argument, namely that urban concentration and innovation go with each other; the present exercise raises the question whether public spending in education that seems to have strong effects on urban concentration stimulates such processes. Even more when urban concentration becomes the engine for growth as noted by Kourtit, Nijkamp (2013).
Furthermore, the analysis of data in point 2 has connections with the contributions of Loannides, Overman (2003), Nitsch (2005), Newman (2005), Giesen et al. (2010), Gómez-Déniz et al. (2014), Gómez-Déniz, Calderín-Ojeda (2015), Shujuan (2016), Luckstead, Devadoss (2017), that tried to find the best distributions to fit better the frequency of cities by size. Actually, although deserving further attention in future works, point 2 shows that Pareto distributions seem to fit most countries of the sample, Log normal distributions are better for countries with remote and small cities and a combination of distributions are the outcome of situations when first cities empty second ones.
Finally, this study confirms that truncated data may lead to strange results as it is demonstrated by Jiang et al. (2015) and Cristelli et al. (2012), as for countries with less number of recorded cities, the Zipf elasticity and Intercept do not seem to be interrelated (see Figure 3).
5 Conclusion
The motivation of this paper is to understand what are the effects in urban concentration of the spatial distribution of rents from natural resources and other unilateral transferences. The methodology used assessed the relation between the Zipf curve elasticity by country and indicators of unilateral transferences by country such as the percentage of the rents from natural resources on the national product, the percentage of education and health expenditures on the national product, the percentages of the net FDI outflows on the national product and the percentage of workers’ remittances on the national product.
Results show that the ownership over natural resources and the spatial distribution of its rents are decisive factors for urban concentration and regional development. Furthermore, when resource rich countries do not consider this, they miss adopting adequate policies of spatial allocation of unilateral transferences. Even education policy has a concentration effect. In future work the location of the cities that are more distant from the estimated Zipf curve requires further attention to look into the factors of spatial justice.
References
Ades A, Glaeser E (1995) Trade and circuses: Explaining urban giants. Quarterly Journal of Economics 110: 195–228. CrossRef.
Anderson GT, Ying G (2005) The size distribution of Chinese cities. Regional Science and Urban Economics 35[2005]: 756–776. CrossRef.
Axtell R, Florida R (2001) Emergent cities: A microeconomic explanation of Zipf’s law. Paper presents at the Society for Computational Economics, Yale University
Benguigui L, Blumenfeld-Lieberthal E (2007) Beyond the power law – A new approach to analyze city size distributions. Computers, Environment and Urban Systems 31: 648–666. CrossRef.
Bertinelli L, Strobl E (2007) Urbanisation, urban concentration and economic development. Urban Studies 44[13]: 2499–2510. CrossRef.
Black D, Henderson V (2003) Urban evolution in the USA. Journal of Economic Geography 4: 343–372. CrossRef.
Bosker M, Brakman S, Garretsen H, Schramm M (2008) A century of shocks: The evolution of the German city size distribution 1925-1999. Regional Science and Urban Economics 38: 330–347. CrossRef.
Brülhart M, Sbergami F (2009) Agglomeration and growth: Cross-country evidence. Journal of Urban Economics 65: 48–63. CrossRef.
Castells M (2012) Networks of Outrage and Hope. Social Movements in the Internet Age. Polity Press, Cambridge, MA
Cordoba J (2008) On the distribution of city sizes. Journal of Urban Economics 63: 177–197
Córdoba JC (2003) On the distribution of city sizes. working paper, Rice University
Cristelli M, Batty M, Pietronero L (2012) There is more than a Power law in Zipf. Scientific Reports 2[1]. CrossRef.
Dentinho TP (2012) New challenges for sustainable growth. In: Capello R, Dentinho TP (eds), Networks, Space and Competitiveness. Evolving Challenges for Sustainable Growth. Edward Elgar, Cheltenham, 276–290. CrossRef.
Dentinho TP (2017) Regional development and migration in the lower basin of the Zambezi river. The importance of property rights. Socio-Economic Planning Sciences 58: 87–102. CrossRef.
Duranton G (2002) City size distribution as a consequence of the growth process. Department of Geography and Environment, London School of Economics
Eaton J, Eckstein Z (1997) Cities and growth: theory and evidence from France and Japan. Regional Science and Urban Economics 27: 443–474. CrossRef.
Gabaix X (1999) Zipf’s law for cities: An explanation. The Quarterly Journal of Economics 114[3]: 739–767. CrossRef.
Gibrat R (1931) Les inégalités economiques. Librairie du Receuil Sirey, Paris, France
Giesen K, Suedekum J (2014) City age and city size. European Economic Review 71: 93–208. CrossRef.
Giesen K, Zimmermann A, Suedekum J (2010) The size distribution across all cities – Double Pareto lognormal strikes. Journal of Urban Economics 68: 129–137. CrossRef.
Gómez-Déniz E, Calderín-Ojeda E (2015) On the use of the Pareto ArcTan distribution for describing city size in Australia and New Zealand. Physica A: Statistical Mechanics and its Applications 436: 821–832. CrossRef.
Gómez-Déniz E, Sordo MA, Calderín-Ojeda E (2014) The Log-Lindley distribution as an alternative to the beta regression model with applications in insurance. Insurance: Mathematics and Economics 54: 49–57. CrossRef.
Henderson JV (2003) The urbanization process and economic growth: The so-what question. Journal of Economic Growth 8: 47–71. CrossRef.
Jiang B, Yin J, Liu Q (2015) Zipf’s law for all the natural cities around the world. International Journal of Geographical Information Science 29[3]: 498–522. CrossRef.
Kourtit K, Nijkamp P (2013) The “New Urban World” – the challenge of cities in decline. Romanian Journal of Regional Science (Special Issue on the New Urban World) 7: 10–28
Krugman P (1996) Confronting the mystery of urban hierarchy. Journal of the Japanese and the International Economies 10: 399–418. CrossRef.
Loannides YM, Overman HG (2003) Zipf’s law for cities: an empirical examination. Regional Science and Urban Economics 33: 127–137. CrossRef.
Luckstead J, Devadoss S (2017) Pareto tails and lognormal body of US cities size distribution. Physica A: Statistical Mechanics and its Applications 465[Supplement C]: 573–578. CrossRef.
Morudu HD (2016) Developing annual population and gross domestic product estimates for local municipality development models in South Africa: Applications of Zipf’s rule from 2001 to 2013. South African Geographical Journal 98[2]: 367–385. CrossRef.
Newman MEJ (2005) Power laws, Pareto distributions and Zipf’s law. Contemporary Physics 46[5]: 323–351. CrossRef.
Nitsch V (2005) Zipf zipped. Journal of Urban Economics 57: 86–100. CrossRef.
Peng G (2010) Zipf’s law for Chinese cities: Rolling sample regressions. Physica A: Statistical Mechanics and its Applications 389[18]: 3804–3813. CrossRef.
Pinto CMA, Lopes AML, Machado JAT (2012) A review of power laws in real life phenomena. Commun Nonlinear Sci Numer Simulat 17: 3558–3578. CrossRef.
Quesnay F (1758) O Quadro Económico. Fundação Calouste Gulbenkian, Lisboa
Shujuan L (2016) Rank-size distributions of Chinese cities: macro and micro patterns. Chinese Geographical Science 26[5]: 577–588. CrossRef.
United Nations (2014) World Urbanization Prospects: The 2014 Revision, Highlights. (ST/ESA/SER.A/352) Department of Economic and Social Affairs, Population Division
Von Thünen J (1826) Der Isolierte Staat in Bezienhung auf Landwirtschaft und Nationalökonomie. Pergamon Press, Oxford. Translated to English by C.M. Wartenberg as “Von Thünen’s Isolated State”, 1966
World Bank (2010) World Bank Open Data. https://data.worldbank.org/
Zipf GK (1949) Human Behavior and the Principle of Least Effort. Addison-Wesley, Cambridge, MA