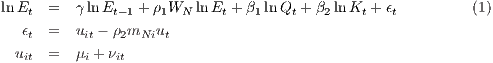Volume
3, Number 2, 2016, 61–69 journal homepage:
region.ersa.org
Volume
3, Number 2, 2016, 61–69 journal homepage:
region.ersa.orgDOI: 10.18335/region.v3i2.164
Regional Science in a time of uncertainty*
1 University of Cambridge, Cambridge, UK (email: bf100@cam.ac.uk) Received: 21 September 2016/Accepted: 10 October 2016Abstract. This paper uses state-of-the-art modelling techniques to simulate possible outcomes for employment across Europe’s regions. The model demonstrates the importance of cross-regional spillovers, and these are an integral part of the simulations. These illustrate what would happen if the current austerity programme remains in force, or possible outcomes if there is a return to pre-2007 ’boom’ conditions. Given that region-specific intervention is a possibility, it is suggested that the methodology of Regional Science is ideally suited to a role of monitoring impacts spilling over to other regions. The paper concludes by emphasising the uncertainty associated with regional prediction and simulation, and highlights the need for a range of possible outcomes.
Key words: spatial econometrics, dynamic spatial panel model, simulation, European regional employment
1 Introduction
I have given this paper the title ‘Regional Science in a time of uncertainty’ because that is what it appears to be, very much a time of uncertainty. Uncertainty is always with us, but what I mean is the future is more uncertain than usual. There are multiple unanticipated and threatening shocks to our economic, social, and environmental systems. For example, global climate change appears to be upon us right now, so what is the future especially for the world’s poorest people, living at the margins of existence? The after-effects of the 2007 shock to the global economy are still very much with us. In an era of very low demand, Central Banks are running out of policy options. We are moving into an era of experimental and unconventional fixes, such as negative interest rates. But these could have dangerous, unanticipated consequences. Also the upheavals in the Middle East are now being manifest as unforeseen mass migrations. Closer to home, the vote to exit the UK from the EU was based on a referendum dominated by claims and counterclaims about the effects of Brexit. Now the UK has voted to leave, the true consequences remain uncertain.
How does Regional Science come into it? We as regional scientists are motivated by a scientific perspective. That means we typically build models that help us make sense of the reality embodied in observable data. These models help us sort out, as best we can, causes and consequences at a ‘regional’ level, where region is a broadly defined concept. Our data relates to space and time, so we observe nations, regions and cities evolving over time.
One big advantage, probably the hallmark of the scientific approach, is the ability to use our models to predict. We might attempt to predict what will happen in the future, or simulate what could, might or should happen in the future, in other words, counterfactual analysis.
I want to focus on the impact of the global economic shock of 2007. Nine years after the event, we are still a long way from what we would consider normality. Global and European demand has fallen and remains persistently low despite Central Banks’ efforts. Because of this persistence, two years ago the European Central Bank became the world’s first major central bank to adopt negative interest rates, a policy also followed by Denmark, Switzerland, Sweden, and Japan. Besides negative interest rates, we are also seeing Government and Corporate Bonds with negative yields.
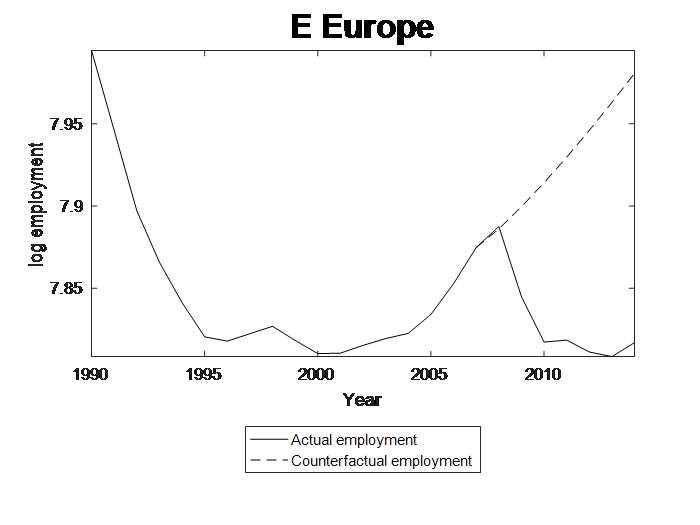
Figure 1 shows what happened to employment across European OECD economies. It also shows the counterfactual, what I think would have happened had the shock not occurred. Evidently, in Western Europe at least, we remain a long way from normality.
2 Model specification
Clearly what the counterfactual is based on is crucial to our interpretation. For a counterfactual, we need a model, preferably driven by theory. My underlying theory has strong post-Keynesian flavour. In other words, the theoretical basis of my analysis is the so-called Verdoorn’s Law (Verdoorn 1949), linking productivity to output and capital stock. This can be written with employment as the dependent variable, and elaborated by introducing temporal and spatial spillovers.
Temporal spillovers mean that employment evolves with a memory, the level of employment this year depends in part on its level last year. This we envisage captures market imperfections which cause employment change to react to the previous change in the drivers of employment. For example, it may take time for extra labour to be fully assimilated into the working practices and technology of employers, or for new capital stock to function effectively.
With spatial spillovers, we assume that the employment level in a given region is not independent of its level in other regions with which there is strong economic interdependence. Economic interdependence is assumed to depend on trade between regions, and is captured by a (time constant) N by N interconnectivity matrix WN, where the N refers to N regions. This interregional connectivity matrix is estimated interregional trade which is based essentially on parameters derived from a model of international trade, following the methodology given in Fingleton et al. (2015), which has its basis in disaggregation methods for time series given by Chow, Lin (1971). The matrix is standardised, as is typical in spatial econometric models, so that each row of WN consists of export shares from a given region to all other regions. Given WN, the model specification is
In equation (1), lnEt is a vector denoting the level of employment at time t in N = 255 NUTS 2 regions of the European Union. The level of employment at time t depends on its previous level at time t - 1, with the strength of this memory effect determined by the parameter γ. It also depends on the contemporaneous employment in other regions weighted by trade-shares as embodied in WN, with parameter ρ1 determining the strength of this interregional spillover effect. The within-region drivers of employment are the levels of output and capital stock within each region, denoted by Qt and Kt, with parameters β1 and β2 respectively.
Unobservable effects are captured by the error term ϵt. The error term is compound, with a time invariant component μi representing the net effect of regional heterogeneity, for example the effect of time-invariant features such as geology, climate, and natural vegetation. In the short term, these vary across space but not across time. In addition we have an idiosyncratic component νit capturing the remaining unobservable effects, varying across both time (t) and space (i).
In our model, the error term is also spatially dependent. In his case we use the N by N connectivity matrix MN which is a matrix of 1s and 0s denoting whether or not regions are contiguous, subsequently row standardised so that rows sum to 1. Assume for example that geology in one region is similar to geology in nearby (contiguous) regions. If adjacent regions have a similar legacy of coal mining, then the effects on economic structure, society and environment, and consequently employment will tend to be similar.
To capture this localised spillover involving the errors, we invoke a moving average spatial autocorrelation process for the errors, as introduced into the panel data literature in Fingleton (2008). This is distinct from the spatial autoregressive process for the direct effect of employment. In the latter, a local change has effects throughout the system of regions, rather than being confined locally as under moving averages. There is an advantage in specifying a moving average spatial error process, because it absorbs local spillovers. Otherwise we might need to consider the spatial lags of right hand side variables, namely WN lnEt-1, WN lnQt and WN lnKt. Incidentally, the estimates produced by such a dynamic spatial Durbin model (see Elhorst 2014) in this instance violate the conditions necessary for model stability.
3 Estimation
What I have briefly described is a dynamic spatial panel model. Further details of the estimation of similar models, but with spatial autoregressive errors rather than spatial moving average errors, are given by Baltagi et al. (2014) and Fingleton et al. (2015). Evidence of consistency of the model with moving average errors is given in Baltagi et al. (2015). To save space I am skipping over the detail of how I estimate this model, which is detailed in these papers, but simply giving the outcome, based on data for the 255 NUTS2 regions for the years 2000 to 2007. As described in Baltagi et al. (2014), estimation is in the spirit of Arellano, Bond (1991), mixing spatial and non-spatial instruments together with a GMM estimator for spatially dependent moving average errors. The estimator with exogenous regressors and a spatial moving average error process works well, as shown by Monte-Carlo experiments (Baltagi et al. 2015). However in this paper we assume endogeneity for all right hand side variables, not simply for the temporal and spatial lags. Bond (2002) gives an accessible description of the methodology, but essentially it involves using a subset of the instrumental variables which are sufficiently lagged in time to avoid correlation with the errors, as is required for instruments. This is important in the case of the Verdoorn law, as detailed below. Because of the reduction in the number of instruments, the estimates differ from what one would obtain if an assumption of exogeneity was made for output and capital. Table 1 shows the differences.
| Exogenous  1t, 1t,  2t 2t | Endogenous
 1t, 1t, 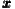 2t 2t | ||||||||||||||
|
variable | para- | param. | std. | t | param. | std. | t
| ||||||||
| meter | est. | err. | ratio | est. | err. | ratio
| |||||||||
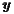 t-1 = ln t-1 = ln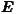 t-1 t-1 | γ | 0. | 6261 | 0. | 01035 | 60. | 48 | 0. | 5222 | 0. | 03309 | 15. | 78 | ||
 N N t = t = 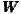 N ln N ln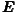 t t | ρ1 | 0. | 2068 | 0. | 01588 | 13. | 02 | 0. | 3702 | 0. | 05675 | 6. | 52 | ||
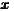 1t = ln 1t = ln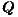 t t | β1 | 0. | 1390 | 0. | 005201 | 26. | 72 | 0. | 1042 | 0. | 02032 | 5. | 13 | ||
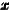 2t = ln 2t = ln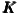 t t | β2 | 0. | 01542 | 0. | 0009967 | 15. | 48 | 0. | 01502 | 0. | 004759 | 3. | 16 | ||
| ρ2 | -0. | 3431 | -0. | 2864 | |||||||||||
| σμ2 | 0. | 5283 | 0. | 5870 | |||||||||||
| σν2 | 0. | 0008 | 0. | 0007 | |||||||||||
Table 1 shows that there are significant temporal and spatial spillover effects, and that the levels of output and capital are also significant determinants of the level of employment. Note that the negative estimate of coefficient ρ2 for the moving averages spatial dependence indicates positive dependence.
The question of which variables were endogenous or exogenous was the subject of a lively debate in some of the earlier Verdoorn law literature, as is evident in the exchange between Kaldor (1975) and Rowthorn (1975b,a), since it is unclear whether output can realistically be treated as exogenous to employment. Assuming endogeneity for all right hand side variables, which is the more conservative stance, does make a difference. It restricts the instrumental variables that can be used, and thus impacts point estimates and increases standard errors, but not so much that the variables become insignificant.
Note that the coefficients for output and capital are positive and significant, but of course we should look at the true derivatives, not the point estimates (Le Sage, Pace 2009, Elhorst 2014). In particular it is noteworthy that the total effect of output on employment in the short run, equal to the direct plus indirect effect, is about 0.17. It appears that in the short run there are increasing returns to scale. However in the long run, the total effect of a persistent 1% increase in output is a 0.97% increase in employment. This suggests that in the long run increasing returns to scale, with higher productivity induced by higher output, is almost wiped out by the spillover effects embodied in our model.
4 Prediction
The prediction equation, given in the standard literature, is
![-1[ ]
lnEˆt = ˆBN ˆγlnEˆt-1 +βˆ1 ln ˜Qt + ˆβ2lnK˜t + ˆHN ¯μ](16422x.png) | (2) |
This is solved recursively. In our case we start with 2008 and predict employment up to 2020.
Of course the predictions are based on many assumptions. One is that the parameter estimates
will remain the same. Second I will assume for the moment that connectivity between regions,
resulting in the spillovers, will also remain the same over the prediction period. So the matrices
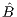 N and ĤN, which take care of the spatial autoregressive process and a spatial moving average
process for the errors, are based on the same trade-based connectivity matrix WN and
on the standardised contiguity MN as used for estimation. But this is optional,
and we could make different assumptions about interregional connectivity for the
future.
N and ĤN, which take care of the spatial autoregressive process and a spatial moving average
process for the errors, are based on the same trade-based connectivity matrix WN and
on the standardised contiguity MN as used for estimation. But this is optional,
and we could make different assumptions about interregional connectivity for the
future.
5 Austerity and Boom scenarios
But for now I will focus on different assumed paths for each region’s output and capital. What could happen to these variables? Let us say that the current policy regime continues, involving monetary policy, quantitative easing, and fiscal policy. Monetary policy in many countries takes the form of low or negative interest rates. Negative interest rates penalize saving, with the hope of stimulating demand. Negative interest rates are not so unreal as a policy option, indeed the European Central Bank already imposes negative interest rates for the Euro area, but currently these only apply to deposits by commercial banks, discouraging them from holding excess cash, and have not, as yet, been passed on to consumers by commercial banks.
Quantitative easing, where a Central Bank creates new money to buy financial assets, like government and corporate bonds, aims to get to a target inflation level of 2%, and is also designed to bring demand back and thus increase employment.
I also assume a continuation of current fiscal policy, in the form of a commitment to a balanced budget and therefore the taxation and spending policies imposed over recent years. For the UK, for example, the target remains a balanced budget, with the ultimate goal a surplus for public finances.
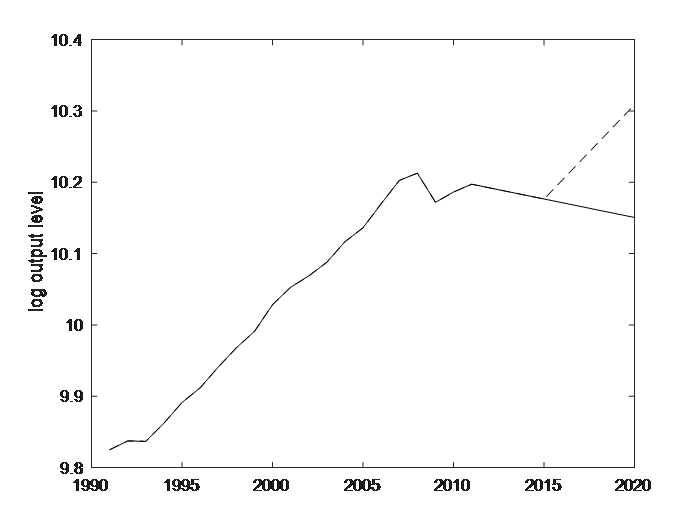
Nevertheless, despite negative interest rates and quantitative easing, we are experiencing continuing austerity. Under a so-called ‘austerity scenario’, the counterfactual path is for every region to maintain its post-2007 downward path for output and for capital. In contrast, under what I call the ‘boom scenario’ we assume that each region’s economy reverts to its 1999-2007 growth rate from 2015. Figure 2 gives the aggregate paths for employment driver’s output and capital stock, summing the region-specific paths over 255 regions.
The downward path under austerity is evident. In contrast we see the upward path under the alternative boom scenario, which is based on each region’s output and capital stock trajectory over the period 1999-2007. During these years, output grew at approximately 2.7% pa taking the mean across the EU regions, while capital stock grew at approximately 3% pa. Under the boom scenario we assume that each region’s economy reverts to its 1999-2007 growth rate from 2015.
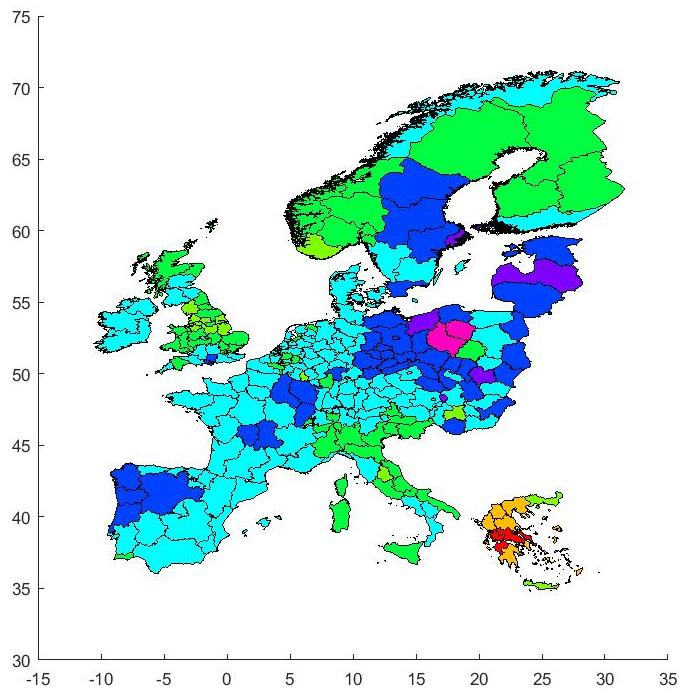
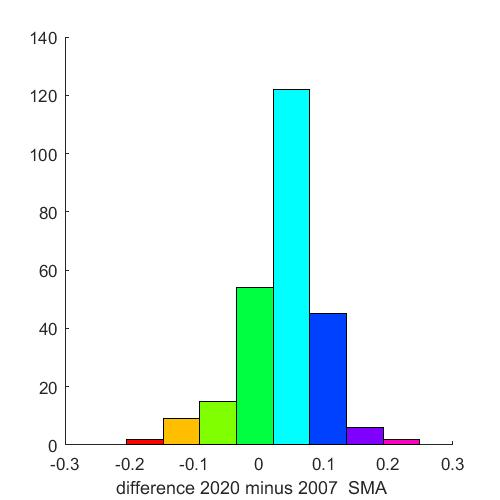
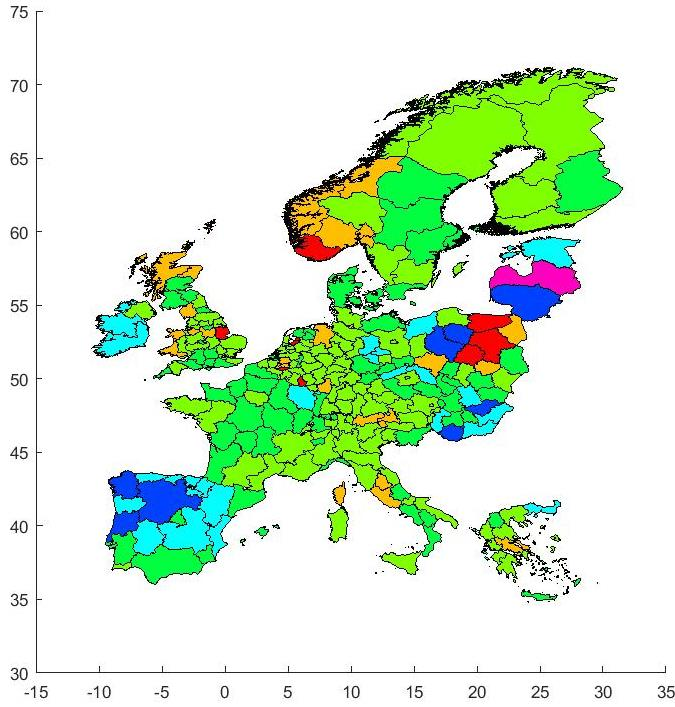
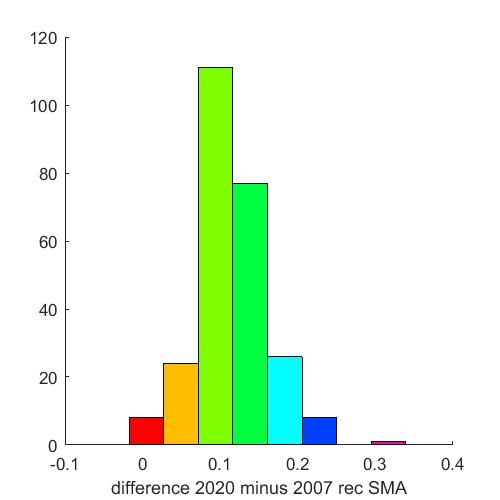
Figure 3 shows the outcomes for employment, giving employment in 2020 relative to 2007 under the austerity scenario. The prospects of continuing austerity is for employment levels in many regions to remain at or below the 2007 level. Figure 4 shows the boom scenario outcome for employment, showing what would happen to employment as a result of the drivers of employment growing at the pre-crisis rate. It shows that by 2020 employment would have reached the 2007 levels or above across all regions. This is good, if it could be achieved. But the recovery would be quite heterogeneous, ranging from about 15% to 20% above the 2007 level in the most buoyant regions, to parity with the 2007 level in the least buoyant. In reality a resurgence of growth of this magnitude, if achievable, would not be the ideal solution with regard to regional equity. While such rapid growth would help eliminate the employment crisis in many regions, especially in Southern Europe, the heterogeneous outcomes could lead to overheating, congestion and inflationary pressures in other regions.
In practice, the policy of negative interest rates by the ECB is not having much effect on growth, and we should not rely on negative interest rates because of the several disadvantages. For example, such a policy could lead to dangerous asset price bubbles, for instance in real estate markets, and destabilize banks as customers choose to stash money in safes or under the mattress! Such a policy could also disadvantage certain regions, since according to Benoît Cœuré, Member of the Executive Board of the ECB, ‘in the euro area, … the negative interest rate policy has distributional consequences across banks located in different jurisdictions,’ because different banks in different jurisdictions might have different capacities to shield borrowers from negative interest rates.
Instead, direct region-specific intervention is necessary in order to alleviate the severe problems of demand-deficit regions. One option, seriously considered in some circles, and not ruled out by ECB President Mario Draghi, is to use what Milton Friedman described as ‘helicopter money’. Conceptually, a helicopter hovers over a region with demand deficit, and drops money directly to individuals, bypassing financial and corporate sectors and going straight to lower and middle income consumers. This would introduce money directly into the income stream, rather than indirectly via negative interest rates working through the banking system. More realistically, this could take the form of regionally specific tax rebates, funded by either printing money or cheap Government borrowing. In this way one could boost demand in deficit regions. Likewise extra Government spending on infrastructure such as roads, bridges, ports, and railroads would ensure extra money is put into circulation. This should be targeted on deficit regions, in order to boost employment and eliminate deflationary tendencies. With borrowing cheap, this would not cost much.
There is one important caveat however. The concept of regional spillovers is well known in Regional Science, and it is likely that intervention targeted in deficit regions will naturally spill over to all regions, and so weaken the desired impact. But in Regional Science we have the tools to be able to estimate and monitor the magnitude, spatial and temporal extent of these leakages to other regions, and so in this way we could provide a valuable service to policy makers in helping them understand the fuller consequences of their actions.
6 Conclusion
To sum up, my counterfactual projections are based on a typical Regional Science model; dependence across time and across space is embedded within the model. It does however have a couple of novel features. First it embodies a spatial moving average error process, and this has the virtue of accounting for local spillovers among the unmodelled variables which are contained within the errors. Otherwise a more complex model, with spatial lags of the right hand side variables would possibly be needed to capture these local spillovers. Secondly, model estimation treats the right hand side variables as endogenous, since output and capital could depend on the level of employment, as well as determine it.
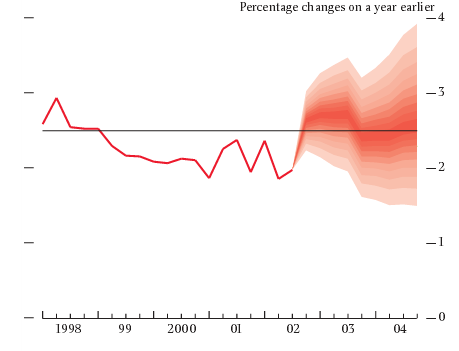
Estimation occurs up to the point at which the 2007 shock occurred, and the parameter estimates obtained form the basis of the projections under austerity and boom scenarios. Of course the projections can be open to question because the model on which they are based can be questioned, and the relationships which held in the historical past, can they be assumed to be valid for the future? Further analysis could explore the robustness of the projections to different assumptions. Ideally our forecasts should be as probability distributions rather than single point forecasts, as exemplified in the Bank of England fan chart in Figure 5. These would emphasise our uncertainty regarding the future, but it is not total uncertainty. In such a way, we can reduce the uncertainty we have about the future, and knowing what might happen under particular assumptions is to me preferable to total uncertainty. To conclude, Regional Science in a time of uncertainty is alive and well and it has an important role to play in helping us to reduce the uncertainty with which we all have to live.
References
Arellano M, Bond S (1991) Some tests of specification for panel data: Monte carlo evidence and an application to employment. Review of Economic Studies 58: 277–297. CrossRef.
Baltagi B, Fingleton B, Pirotte A (2014) Estimating and forecasting with a dynamic spatial panel data model. Oxford Bulletin of Economics and Statistics 76: 112–138. CrossRef.
Baltagi B, Fingleton B, Pirotte A (2015) Estimating and forecasting with a dynamic spatial panel data model under spatial moving average errors. mimeo
Bond S (2002) Dynamic panel data models: a guide to micro data methods and practice. Portuguese Economic Journal 1: 141–162. CrossRef.
Chow G, Lin Al (1971) Best linear unbiased interpolation, distribution, and extrapolation of time series by related series. The Review of Economics and Statistics 53: 372–375. CrossRef.
Elhorst JP (2014) Spatial Econometrics: From Cross-Sectional Data to Spatial Panels. Springer, Heidelberg. CrossRef.
Fingleton B (2008) A generalized method of moments estimator for a spatial panel model with an endogenous spatial lag and spatial moving average errors. Spatial Economic Analysis 3: 27–44. CrossRef.
Fingleton B, Garretsen H, Martin RL (2015) Shocking aspects of monetary union: The vulnerability of regions in Euroland. Journal of Economic Geography 15: 907–934. CrossRef.
Kaldor N (1975) Economic growth and Verdoorn’s law: a comment on Mr Rowthorn’s article. Economic Journal 85: 891–896. CrossRef.
Le Sage J, Pace K (2009) Introduction to Spatial Econometrics. Taylor and Francis. CrossRef.
Rowthorn RE (1975a) A reply to Lord Kaldor’s comments. Economic Journal 85: 897–901. CrossRef.
Rowthorn RE (1975b) What remains of Kaldor’s law? Economic Journal 85: 10–19. CrossRef.
Verdoorn PJ (1949) Fattori che regolano lo sviluppo della produttivita del lavoro. L’Industria 1 translated by AP Thirlwall. In: Ironmonger D, Perkins J, Hoa T (eds), National Income and Economic Progress: Essays in Honour of Colin Clark. (1988) Macmillan, London. CrossRef.