 Volume
4, Number 1, 2017, 109–127 journal homepage:
region.ersa.org
Volume
4, Number 1, 2017, 109–127 journal homepage:
region.ersa.orgDOI: 10.18335/region.v4i1.107
Revisiting the Boston data set – Changing the units of observation affects estimated willingness to pay for clean air
1 Norwegian School of Economics, Bergen, Norway, (email: roger.bivand@nhh.no); Adam Mickiewicz University, Poznań, Poland Received: 2 December 2015/Accepted: 6 April 2017Abstract. Harrison, Rubinfeld (1978c) used a hedonic model to find out how house values were affected by air pollution in Boston, when other variables were taken into consideration. Their primary interest was in estimating willingness to pay for cleaner air. They chose to use 506 census tracts as units of observation because median house values for these units of aggregation were published in the 1970 census tabulations. Air pollution values from the model output, represented by nitrogen oxides (NOX), were available for 122 model output zones, of which only 96 fell within the study area defined by the chosen census tracts. These NOX values were then assigned proportionally to all census tracts falling within each model output zone. By re-aggregating the house value data to the 96 air pollution model output zones and re-fitting the regression model, the total impact of air pollution on house values, and thus the estimated willingness to pay, increases markedly. By extending the analysis to include spatially lagged independent variables, the total impact of air pollution on median house values, and consequently on the willingness to pay analysis, increases by over three times. Use of weighting to adjust the units of observation for the relative numbers of housing units behind each median house value further buttresses this conclusion. It is shown conclusively that the choice of observational units matters crucially for the estimation of economic parameters of interest in this data set.
1 Introduction
The Harrison, Rubinfeld (1978c) Boston housing data set has been widely used because of its availability from Belsley et al. (1980) and Statlib, and was further discussed by Pace, Gilley (1997) and Gilley, Pace (1996). The original paper has been highly cited, with almost 400 journal references, mostly by data analysts using the original data set for testing estimation methods, rather than by environmental or urban economists. The underlying research question was the estimation of willingness to pay (WTP) for clean air, using air pollution levels and house values in a hedonic regression (see also Harrison, Rubinfeld 1978b,a, which are not highly cited). Differences in house values for otherwise similar observations but differing pollution levels should permit the estimation of a coefficient for the calibration of WTP for clean air. As Pace, Gilley (1997, p. 337) showed clearly, the air pollution coefficient estimate in their fitted models changed when residual spatial autocorrelation was taken into account (from -0.0060 to -0.0037), as did its standard error (from 0.0012 to 0.0016).
Repeated attempts to fit spatial econometrics models to the 506 observations of census tracts in the original data set, and to take account of censoring as noted by Gilley, Pace (1996), have not resolved the question of what WTP would be in a model not subject to serious mis-specification issues. The modelled data set suffers from spatial autocorrelation in many ways, as well as heteroskedasticity, and there are further questions about functional form.
The use of spatial econometrics models described by Halleck Vega, Elhorst (2015) and LeSage (2014) including the spatially lagged dependent variable, spatially lagged errors, and spatially lagged independent variables does not seem to be successful. The best fit is achieved with the General Nested Model (GNM), with the total impact reaching -0.0093, somewhat larger than the least squares coefficient value (-0.0066), but much less significant. The levels of autocorrelation seen in the air pollution variable are very high, something which could have a reasonable basis in the data generation process of the variable, but which deserves investigation. Attempting to instrument for the possible errors-in-variable status of the air pollution variable, as suggested by Anselin, Lozano-Gracia (2008) using methods provided by Drukker et al. (2013) and Piras (2010) also results in unsatisfactory outcomes: the air pollution total impact is insignificant and positive (0.0042) in a GMM SARAR model with air pollution taken as subject to errors-in-variables and instrumented by a quadratic trend surface.
The levels of spatial autocorrelation present in the GNM are very large and highly significant (ρLag = 0.7436, ρErr = -0.2842),1 but do not have any clear economic interpretation. Dropping the spatially lagged independent variables from the model yields equally significant spatial coefficients, but with a sign flip (ρLag = 0.2808, ρErr = 0.4889). These results mirror those found in the GMM SARAR with the air pollution subject to errors-in-variables, with spatial coefficients large in absolute value and highly significant (ρLag = 0.3867, ρErr = 0.3645).
In revisiting the Harrison, Rubinfeld (1978c) Boston housing data set in this study, an attempt will be made to establish the reason for the presence of this very strong spatial autocorrelation. Gibbons, Overman (2012) argue that spatial econometrics is too often applied without sufficient consideration of the underlying economics; in this paper, we will rather consider the configuration of the units of observation. Is the strength of spatial autocorrelation observed in this data set a feature of the census tract observations themselves, or has it been introduced or strengthened by changes in the observational units used for the different variables? Our focus will be on the choices of observational entities made in assembling the original data set, and on an alternative that arguably should be more relevant for the data generation process of the air pollution variable. Having re-established an approximation to the model output zones from which the air pollution variable levels were taken, it will be shown that much of the puzzling spatial autocorrelation is removed. A further question to be considered is whether weights should be used to account for the very different numbers of housing units found in each observational entity, taking up the challenge given by Solon et al. (2015).
2 Observation entities in Harrison, Rubinfeld (1978c)
In order to approach WTP for cleaner air, Harrison, Rubinfeld (1978c) used a hedonic regression including air pollution levels with house values as the dependent variable. They use a data set for most of the Boston SMSA in 1970 at the census tract level of aggregation. The data were made available by Belsley et al. (1980, pp. 229–261) in the form in which they appear to have been analysed. Pace, Gilley (1997) and Gilley, Pace (1996) found that there were errors in Belsley et al. (1980) and the Statlib data file, and that the house value data were censored.
2.1 House values
Harrison, Rubinfeld (1978c) used median house values in 1970 USD for 506 census tracts in the Boston SMSA for owner-occupied one-family houses; census tracts with no reported owner-occupied one-family housing units were excluded from the data set. Here the values are not at the micro-level but medians from census tracts from the 1970 US Census (for “owner-occupied one-family housing”). The relevant question is H11: “If you live in a one family house which you own or are buying — What is the value of this property? That is, how much do you think this property (house and lot) would sell for if it were for sale?”2 . H11 was answered by crossing off one grouped value alternative, ranging from under $5,000 to over $50,000. Tracts with weighted median values in these upper and lower alternative value classes are censored. The house value data have census tract support, and are median values calculated from group counts from the alternatives offered in H11.
The published census tract tabulations show the link between question H11 and the Statlib-based data (after correction).3 The median values tabulated in the census report can be reconstructed from the tallies shown in the same Census tables fairly accurately using the weightedMedian function in the matrixStats in R, using linear interpolation, and midpoint values of $3,500 and $60,000 for the left- and right-censored intervals.4
Two tracts are entered as having a median house value below $5,000, and 15 have median values over $50,000, as was pointed out by Gilley, Pace (1996). One tract has a median of exactly $50,000, with 31 houses below the right-censored boundary, and 31 above. Having access to the Census value group counts by tract means that alternative aggregations of house value — the dependent variable in the analysis — may be constructed using the underlying data.
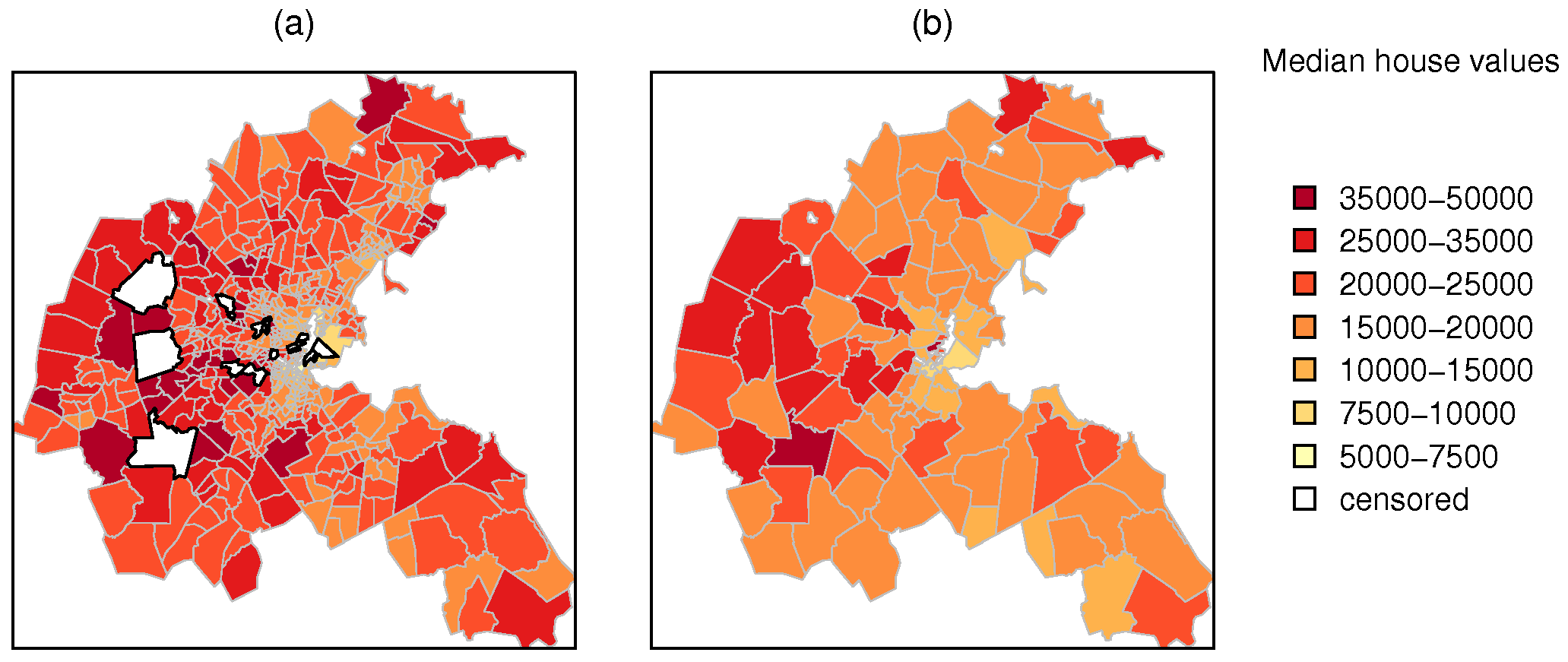
The effectiveness of the study was prejudiced by the fact that areas of central Boston with the highest levels of air pollution also lose house value data, either because of tract exclusion (no one-family housing units reported) or right or left censored tracts. Figure A.2 shows the impact of censoring in central Boston, where the highest air pollution values were predicted, with few tracts represented by weighted median house values. The excluded tracts contained no owner-occupied one-family housing units, or too few to tabulate, but may have included rented housing, which was not considered in the original study.
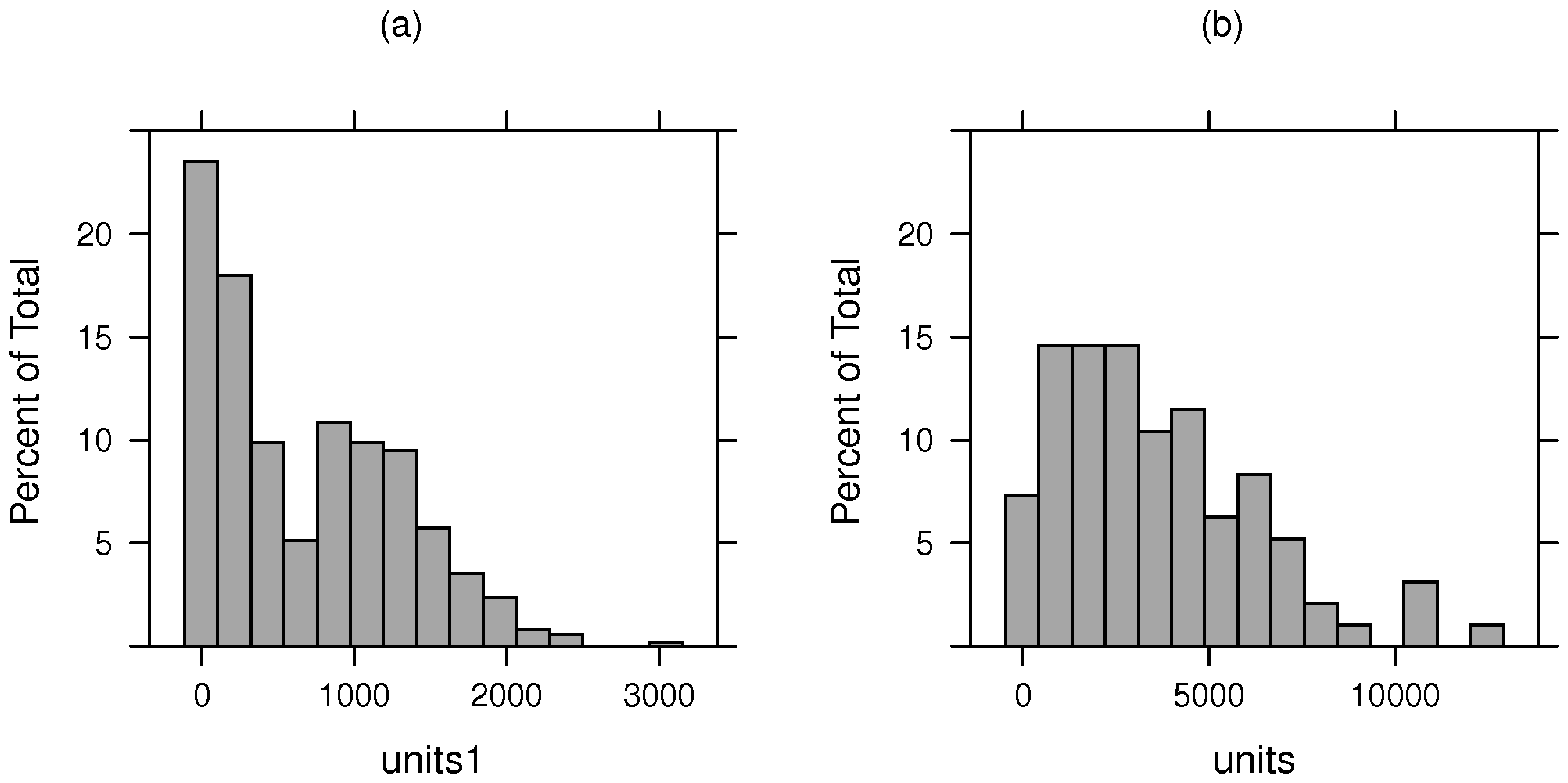
A further point made by Harrison, Rubinfeld (1978c, pp. 88, 98–101), is that the number of housing units by tract varies greatly. They tried using weighted regression, using the logarithm of the counts of one-family houses by tract as the weighting variable, and noted some change in coefficient values. This step was taken to attempt to check the results for robustness to heteroskedasticity. Figure A.5 and Table 1 show the considerable disproportions present in the data, both for the original choice of census tracts as observational units, and for the alternative Transportation and Air Shed SImulation Model (TASSIM) zones proposed below.
| minimum | lower | median | upper | maximum | |
| quartile | quartile | ||||
| 506 Census tracts | 5.00 | 115.00 | 511.50 | 1155.00 | 3031.00
|
| 96 TASSIM zones | 25.00 | 1624.00 | 2926.50 | 5189.50 | 12411.00
|
The data used by Harrison, Rubinfeld (1978c) took the census tract as the observational unit as we have seen. The US Census is organized using a nested system of blocks, block groups and tracts. Data for house value counts for blocks are often not available because the numbers in each value group are too small for publication. Table A.1 shows the relative distribution of counts of blocks and housing units per block based on data extracted from the National Historical Geographic Information System.5 The choice of census tracts by the original authors as the smallest feasible areal unit seems justified, especially as most of the other variables they used were not available at the block level, especially air pollution.
2.2 Air pollution
The data on air pollution concentrations were obtained from the Transportation and Air Shed SIMulation model (TASSIM) applied to the Boston air shed (Ingram, Fauth 1974). That study was conducted to simulate the possible consequences of abatement policies affecting road traffic. It used data on vehicle and point-source emissions combined with meteorological data to generate a number of mean air pollution concentration surfaces, which were then calibrated to values from monitoring stations. The calibrated model results were obtained for 122 zones, and assigned proportionally to the 506 census tracts. Values were taken for particulate matter (PART) and nitrogen oxides (NOX), and analysis proceeded using only NOX. The NOX values in the published data sets are in units of 10 ppm (10 parts per million), and were then multiplied by 10 again in the regression models to yield parts per 100 million (pphm).6
Many of the smaller tracts belong to the same TASSIM zones; this is a clear case of change of support, with possibly different spatial statistical properties under the two different entitation schemes (Gotway, Young 2002). Harrison, Rubinfeld (1978c, p. 86, footnote 14) do comment that “… the true correlation between NOX and PART is somewhat overstated because the TASSIM model generates data for 122 zones, not 506 census tracts. Translating zonal data into census tracts tends to overstate the correlation because relatively more census tracts are located in center city zones in which PART and NOX levels tend to be most highly correlated.” This is not directly related to the modifiable areal unit problem (Wong 2010); the relationship between this case and the modifiable areal unit problem will be discussed in the conclusion below.
Since the data set from Belsley et al. (1980) does not include PART, nor the identifiers of the TASSIM zones underlying the assignation of copied values to census tracts, it is not possible from the data as they stand to retrieve the zones with full certainty. We can, however, aggregate contiguous census tracts with identical values of NOX, giving 96 approximated TASSIM zones, for which we can aggregate grouped house value counts, and calculate median values using the same procedure as that used at the census tract level of resolution.
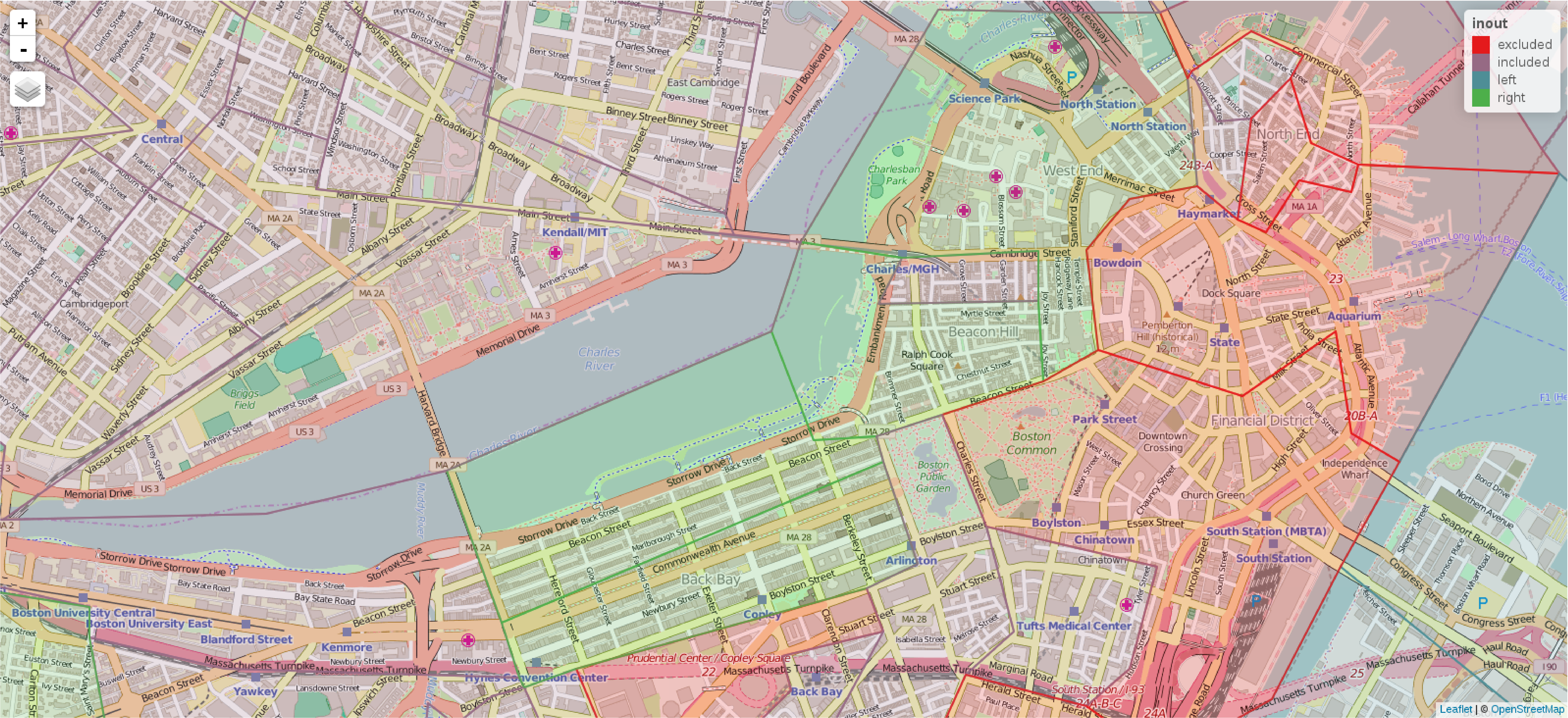
A two-part report7 details the use of the TASSIM simulation model (Ingram, Fauth 1974, Ingram et al. 1974). Both of these volumes include line-printer maps of the TASSIM zones, and the Fortran code in volume 2 (Ingram et al. 1974, pp. 183–185) shows the links between the 122 TASSIM zones and the line printer output. There is no description of the projection used, so relating these polygons to tract boundaries is not exact. Western TASSIM zones appear to lie outside the Boston SMSA tracts included in the 506 census tract data set. An affine transformation between ground control points in the map of 506 census tracts, and guessed equivalents in the line printer TASSIM zones is shown in Figure A.3. The remaining discrepancies appear to come from merging contiguous census tract data set entities with the same NOX values which actually belonged to more than one TASSIM zone, and from poor matching because of difficulties in locating ground control points on the line printer output map; there are few discrepancies remaining, less than ten percent of the TASSIM zone entities.
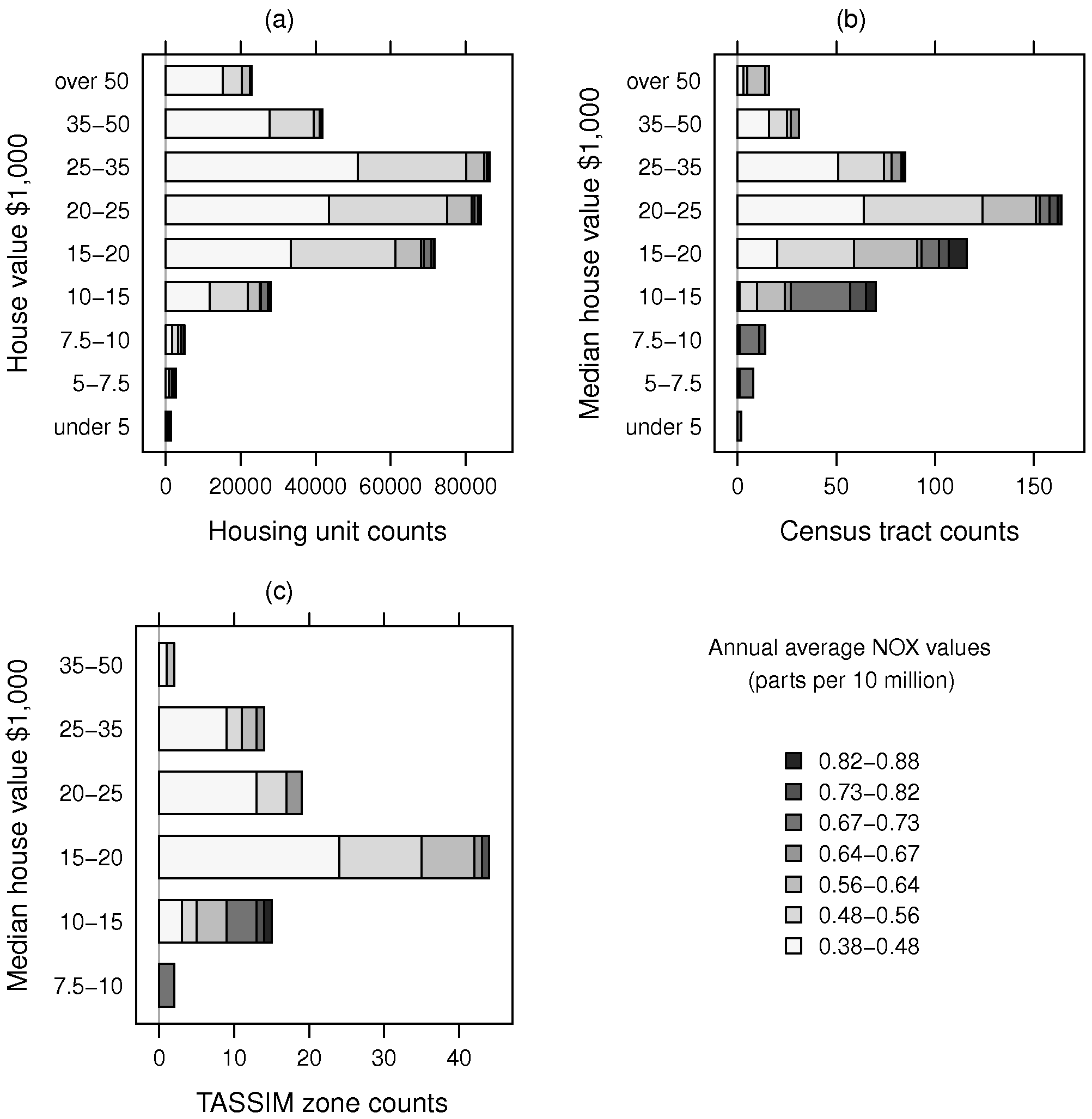
Figure 1 uses grey shades to visualize the possible impact of using weighted regression, with panel (a) showing — with the chosen class intervals for NOX — the actual relationship between house value and NOX. The NOX levels and house value class counts are taken from the census tract data set. In the remaining panels, the bar lengths are proportional to the counts of spatial entities with median house values falling into the H11 house value classes. NOX fill shades represent levels of air pollution. Tracts and TASSIM zones with higher levels of air pollution typically have many fewer housing units. It can be seen that the numbers of housing units with higher levels of air pollution are proportionally less in (a) than in (b) or (c), and that the largest value class for housing units was $25,000–35,000, for $20,000–25,000 for census tracts, and $15,000–20,000 for approximate TASSIM zones. An argument for weighing the hedonic regressions is to shift the interpretative basis back to that of panel (a), that is the actual numbers of housing units subject to different levels of air pollution.
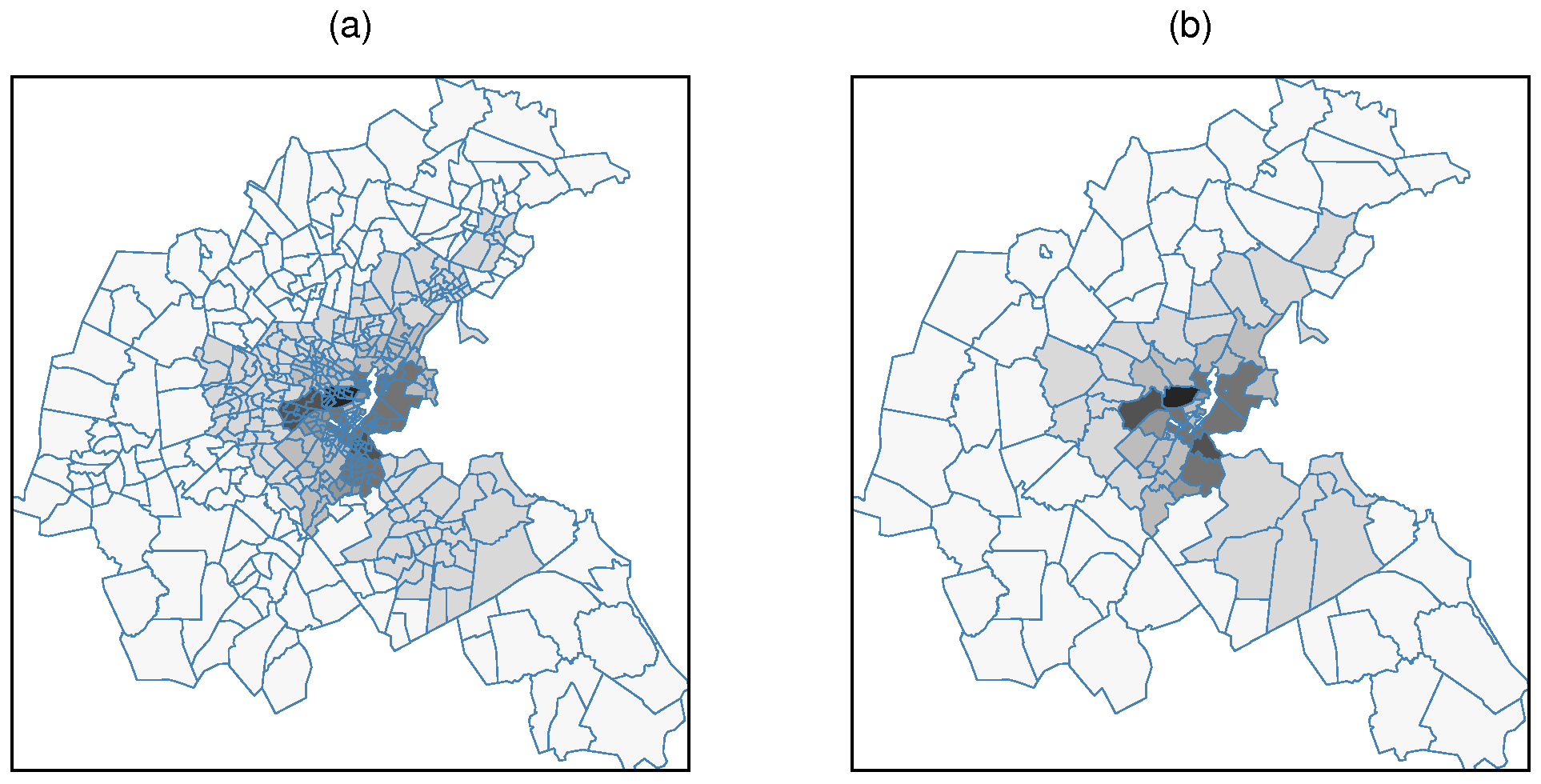
Figure 2 shows clearly that the study of the relationship between NOX and house value will be impacted by “copying out” NOX values to census tracts, as noted by Harrison, Rubinfeld (1978c, p. 86, footnote 14) and mentioned above. Even if we were to use more class intervals in these choropleth maps, the visual impression would be the same, because the underlying data have support approximated by the 96 TASSIM zones, not by the 506 census tracts.
Figure A.4 shows changes in the visual impression given by aggregating the H11 median house value counts to approximate TASSIM zones before calculating interpolated weighted median values. It also shows the censored census tracts for which we have no reliable median values, as the values taken depend on the assumed under/over interval midpoints. Once we aggregate to TASSIM zones, there are no longer any censored median values, because the weighted medians no longer fall outside the bounded range between $5,000–50,000.
2.3 Other independent variables
Besides NOX, the other census variables included in the hedonic regression to account for median house values are the average number of rooms per house, the proportion of houses older than 1940, the proportion low-status inhabitants in each tract, and the Black proportion of population in the tract — originally expressed as a broken-stick relationship, but here taken as a percentage. The crime rate is said to be taken from FBI data by town, but which is found on inspection to vary by tract. The distance from tract to employment centers is derived from other sources, as is the dummy variable for tracts bordering Charles River.
Other independent variables are defined by town, with some also being fixed for all towns in Boston. The town aggregates of census tracts are used in many of the census report tabulations, and of the 92 towns, 17 only contain one census tract, while one town contains thirty census tracts. The variables are the proportion of residential lots zoned over 25,000 sq. ft, the proportion of non-retail business acres, accessibility to radial highways, full-value property-tax rate per $10,000, and pupil-teacher ratio by town school district. These variables are also “copied out” to tracts within towns, but do not coincide completely with the approximate TASSIM zones. In the case of 80 approximate TASSIM zones aggregated from census tracts, the boundaries do coincide exactly with town boundaries. However, for the remaining 12 towns and 16 TASSIM zones, there are overlaps between more than one town and TASSIM zone, mostly in Boston itself. The exact match between town boundaries defined using census tracts, and approximated TASSIM zones also constructed using census tracts is not necessarily an indication that towns were used as TASSIM zones, but as we cannot reconstruct the actual model output zones exactly, we assume that the difference is without importance for this study. Using TASSIM zones for analysis should therefore also reduce the levels of autocorrelation induced by “copying out” town values to tracts within towns.
Table A.2 shows the descriptive statistics for the variables used in the 489 observation census tract data set omitting tracts with censored median house values. These covariates were aggregated to approximate TASSIM zones using weighted averages, where the weights are the tract population counts. The Charles River dummy was aggregated by taking the maximum value of any tract included in the approximate TASSIM zone. It would be possible to punch8 more census data for some of the variables, but not all the variables used are present in the census tables available online. Table A.3 shows the descriptive statistics for the variables used in the 96 observation approximate TASSIM zone data set.
3 Applying weighted spatial econometrics models to the Boston data sets
Pace, Gilley (1997) felt that it should be worthwhile to check whether the original model was spatially misspecified. They considered that the use of spatial aggregate units as observations might involve spillovers of some kind, chiefly in the house values used – neighboring census tracts may have similar values for a number of reasons. Had the included explanatory variables accounted for the similarities between neighbors, there might not have been any reason to go further, but the residuals were found to be spatially highly patterned. So now we will turn to spatial econometrics methods to try to unravel the question of the “real” link between house values and NOX. We use row-standardized contiguity neighbors derived from the map of census tracts, omitting the censored tracts which leads to one tract having no neighbors, and from the map of merged census tracts constituting approximate TASSIM zones.
3.1 Spatial econometrics models with case weights
The models chosen here are unweighted and weighted variants of least squares (OLS) and the spatial error model (SEM), both also extended by including spatially lagged independent variables (SLX and SDEM respectively). The arguments for and against the use of weights have been reviewed recently by Solon et al. (2015). They distinguish between situations in which the analyst is most interested in estimating descriptive statistics for a population, and the estimation of causal effects, for example through correcting for heteroskedasticity. It may be argued that the hedonic model used by Harrison, Rubinfeld (1978c) is less concerned with establishing the causal effect of air pollution on house values than with estimating the coefficient expressing how house values would respond to changes in air pollution, thus providing insight into WTP for clean air. Given the very large variations in counts of housing unit valuations underlying each median value demonstrated above, it seems reasonable to consider the numbers of housing units by observation as case weights (it was noted above that Harrison, Rubinfeld (1978c, pp. 88, 98–101) checked logarithms of these counts as weights in a robustness test but found little difference from OLS).
There are two reasons for choosing not to include the spatially lagged median house value dependent variable in the models considered. The first is based on LeSage (2014), and the probability that the aggregate nature of the dependent variable makes it seem more reasonable to consider local spillover specifications. The “copying out” of covariates across multiple tracts from the different entitation schemes for TASSIM output zones and for towns can arguably be seen as being better represented by local rather than global spillovers. The second reason is pragmatic, that weighted spatial regression code in the spdep package in R is so far only implemented for the spatial error (SEM) and by extension the spatial Durbin error model (SDEM).9
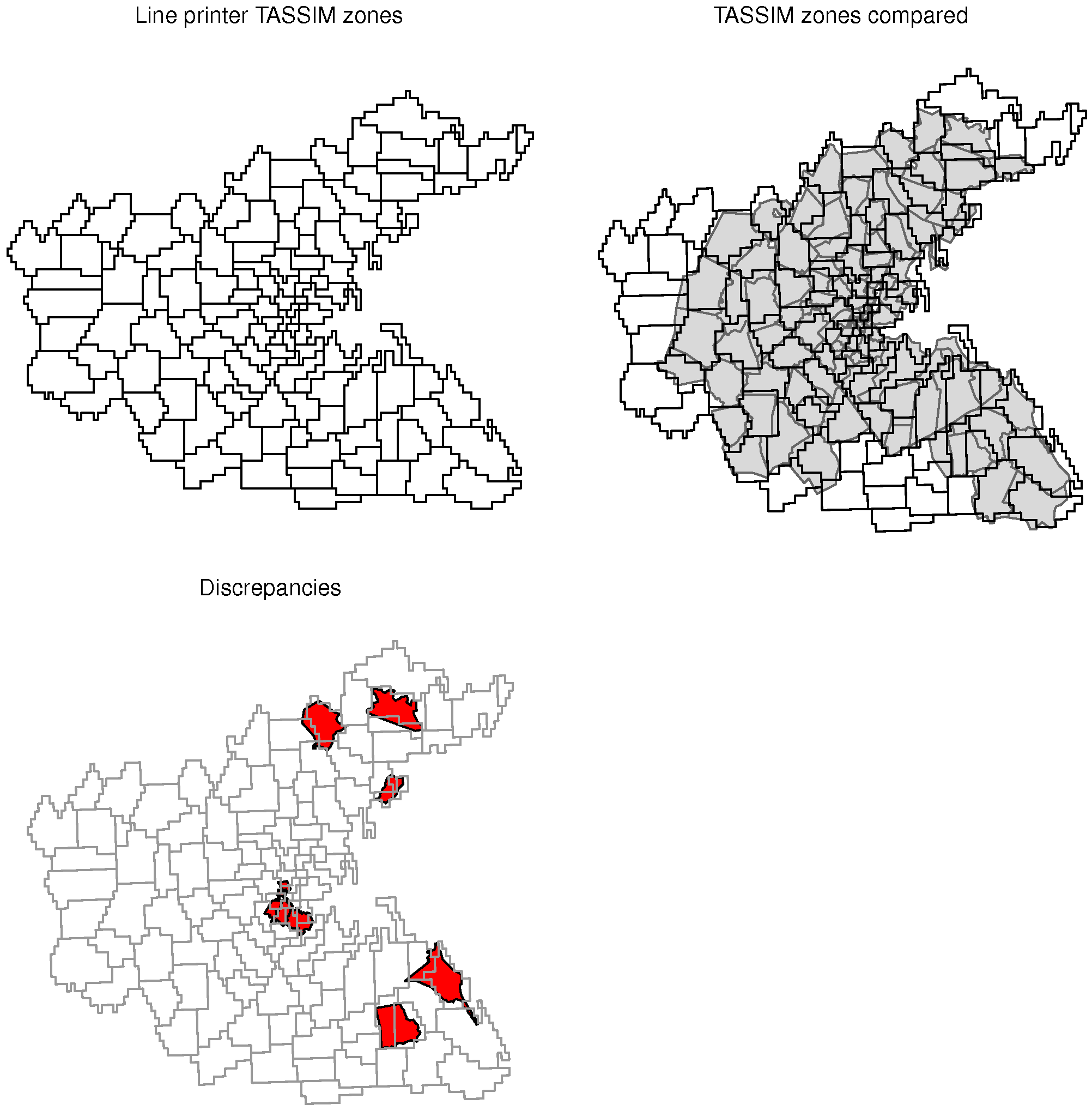
The dependent variable representing house value is taken as the logarithm of median house values in 1970 USD, and the air pollution variable is the square of NOX in parts per hundred million; these and all other variables are represented as in the original study (with the exception of the Black proportion of population). We will now present briefly the models used. Assuming that the variance of the disturbance term is constant, we start from the standard linear regression model:
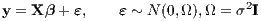
where y is an (N × 1) vector of observations on a dependent variable taken at each of N locations, X is an (N ×k) matrix of exogenous variables, β is an (k × 1) vector of parameters, and ε is an (N × 1) vector of disturbances. The spatial error model (SEM) may be written as (Ord 1975):
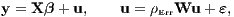
where y is an (N × 1) vector of observations on a dependent variable taken at each of N locations, X is an (N ×k) matrix of exogenous variables, β is an (k × 1) vector of parameters, ε is an (N × 1) vector of disturbances and ρErr is a scalar spatial error parameter, and u is a spatially autocorrelated disturbance vector with constant variance and covariance terms specified by a fixed (N × N) spatial weights matrix W and a single coefficient ρErr:
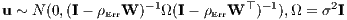
In both cases, the Durbin forms (SLX, SDEM) are defined by augmenting the matrix of independent variables X with its spatial lag WX, now using [X,WX] instead of just X (the intercept is included only once in the case of row-standardized spatial weights). The weighted versions are formed by altering Ω = σ2I by replacing the identity matrix by a diagonal matrix of the inverses of known case weights reflecting the relative “size” of the observations (Waller, Gotway 2004). The variance term σ2 is still estimated, but with the assumption of uniform variance replaced by variance proportional to the inverse of known case weights.
3.2 Model diagnostics
Comparison of models fitted using different models to different aggregations of the same data may be handled qualitatively, as there does not seem to be an agreed basis in statistics or econometrics from which to proceed. The Durbin versions of OLS and SEM will subsequently be termed SLX and SDEM (LeSage 2014, Halleck Vega, Elhorst 2015). The weighted and unweighted OLS and SLX models were fitted by least squares, and the weighted and unweighted SEM and SDEM models were fitted by maximum likelihood. The SDEM model nests the others: OLS, SLX and SEM, but SEM only nests OLS, not SLX. The values of likelihood ratio tests are shown in Table 2 by data set and the use of weighting. In the 489 census tract data set, the SDEM model appears to be dominant in both the weighted and unweighted cases, while the SLX model appears to dominate in the 96 TASSIM zones data set.
| TASSIM | TASSIM | Census | Census | |
| weighted | weighted | |||
| OLS:SLX | 4.685e-09 | 5.246e-05 | < 2.2e-16 | 1.045e-11
|
| OLS:SEM | 0.06099 | 0.0009402 | < 2.2e-16 | < 2.2e-16
|
| OLS:SDEM | 1.062e-08 | 9.246e-05 | < 2.2e-16 | < 2.2e-16
|
| SLX:SDEM | 0.789 | 0.6512 | < 2.2e-16 | < 2.2e-16
|
| SEM:SDEM | 1.966e-08 | 0.002528 | 1.388e-10 | 6.28e-05
|
More complete tables of diagnostic tests for groups of models are presented in the Appendix below, but discussed briefly here. Tables A.4 and A.5 show the AIC values for fitted models for two sets of entities: 489 census tracts and 96 approximate TASSIM zones, and approximately the same data. These values, although also based on the log likelihood, penalize models with more independent variables, here the SLX and SDEM models including the spatially lagged independent variables. The data for median house values are constructed in exactly the same way, as is the air pollution variable, while other variables for TASSIM zones are population-weighted aggregates of the values in the census tract data set. The best model fit may be held to be indicated by the lowest AIC value among comparable models.
In Table A.5, the spatial error models no longer outperform the models without a spatially lagged error term, and the spatial coefficients of the spatial error models are not significant (see Table A.10). The SLX models do outperform their non-weighted counterparts, subject to the remark above about the comparability of these models. If we prefer the census tract data set, we might conclude that the weighted SDEM model is to be preferred, but if we choose the approximate TASSIM zones, our choice would be the weighted SLX model, including the spatially lagged independent variables.
Table A.6 shows Breuch-Pagan tests for heteroskedasticity for models fitted by least squares; columns 3 and 4 test against housing unit counts per aggregate entity as the source of heteroskedasticity. The OLS and SLX fitted models for the 489 census tracts show strong heteroskedasticity, which is reduced but not removed when modelled by housing unit counts. For the two models fitted using the 96 TASSIM zones, heteroskedasticity is only present for OLS, but not for SLX, and weighing with housing unit counts largely removes heteroskedasticity.
Standard deviates of Moran’s I test for spatial autocorrelation in least squares regression residuals for weighted and unweighted OLS and SLX models are shown in Table A.7. All the test results for the 489 census tract data set are highly significant, while only the 96 TASSIM zones weighted OLS model residuals show any significant residual autocorrelation using this test. Table A.8 adds to this for the unweighted models estimated using least squares, showing the results of robust Lagrange multiplier tests. For the 96 TASSIM zones data set, only the robust test for an omitted lag coefficient is borderline significant, while all the robust tests for the 489 census tract data set were highly significant apart from the robust test for an omitted spatial lag coefficient for the SLX model.
Using the Hausman test given by Pace, LeSage (2008), and extended for case weights, it is found that all the tests for the 489 census tract data set for spatial and spatial Durbin error models (SEM, SDEM), whether weighted or not, reject the null hypothesis of no differences between least squares and spatial model coefficients on independent variables. In the case of the 96 TASSIM zones data set, only the test result for the unweighted SEM model is significant (Table A.9). Finally, Table A.10 shows spatial coefficient ρErr values and Wald test p-values for spatial error and spatial Durbin error models. All the ρErr values are highly significant for the 489 census tract data set, but only the SEM (both weighted and unweighted) ρErr values are significant for the 96 TASSIM zones data set.
Based on these diagnostics, it is clear that all the models fitted for the 489 census tract data set have serious mis-specification issues, and that the models fitted for the 96 TASSIM zones data set appear to be more successful, especially those including the spatially lagged independent variables, whether weighted or not.
3.3 Interpretation of model results
While we cannot directly compare relative model mis-specification across the two sets of entities (census tracts and approximate TASSIM zones), we can compare coefficient values for the key variable of interest, air pollution, taken as the square of NOX in the original scaling (parts per hundred million, pphm). For brevity, and because our focus here is on the consequences of choices of units of observation for estimates of the air pollution coefficient, other results are not given here, but may be obtained from the reproduction code. Note that by reducing the number of observations by a factor of five, the standard errors of the TASSIM zone coefficients are made much larger by construction. Further, note that standard errors reported below for the SEM and SDEM models are maximum likelihood estimates corrected by multiplication by N∕(N - k) for comparison with OLS and SLX standard error estimates.
Panel (a) of Figure 3 shows the coefficient values and 95% standard error bars for eight models excluding spatially lagged independent variables. The result for the unweighted SEM model for the census tract data set is not dissimilar from that given by Pace, Gilley (1997). The effect of residual spatial autocorrelation on the standard errors (and indeed on the coefficient values) is shown by comparing the OLS and SEM results for the census tract data set, regardless of whether weights are used.
When we move our attention to the Durbin models, including the spatially lagged covariates, we begin to be able to discern the consequences of the choice of observational units for inference about the air pollution variable. Panel (b) of Figure 3 shows the direct impacts, which are the NOX coefficient values from eight models. In the case of the 489 census tract data set, the coefficient values are positive and insignificant. For the 96 approximate TASSIM zones, the values are negative, as expected, and significant. It is the choice of observation units that makes the greater difference, larger than the inclusion or not of a spatial process in the disturbances, and larger than the inclusion or not of case weights to treat heteroskedasticity.
Panel (c) of Figure 3 shows the indirect impacts (the coefficients on the spatially lagged air pollution variable) and 95% times their standard errors. All are negative and the 489 census tract data set models are all significant. The standard errors of the 489 census tract NOX coefficients are much smaller than those of the models fitted using the 96 approximate TASSIM zones data set, not just because of the difference in numbers of observations. The NOX indirect impacts for the weighted models fitted using the 96 approximate TASSIM zones data set are at best marginally significant, so that with this data set and weighted regression, most of the “action” is in the direct impacts.
Finally, panel (d) of Figure 3 shows the total impacts for the eight models including the spatially lagged covariates, calculated using linear combination of the fitted model results for the NOX variable and its spatial lag. The total impact is simply the sum of the coefficient values, but the standard errors are calculated using the estimable function in the R gmodels package. The models fitted using the two different choices of observation entities differ considerably, with strong residual spatial autocorrelation in both the weighted and unweighted SLX models for the census tracts data set (see also TableA.10). The SDEM spatial autoregressive coefficients ρErr for the census tracts data set are 0.658 (standard error 0.0416) for the unweighted model and 0.62 (standard error 0.0444) for the weighted model. The equivalent values for the SDEM models for the approximate TASSIM zones data set are 0.0562 (standard error 0.155) for the unweighted model and 0.0964 (standard error 0.153) for the weighted model. The choice of observation entities is driving the value of the spatial error coefficient and inference on the appropriateness of its inclusion.
If we choose the approximate TASSIM zones data set, and drop the SDEM specification including ρErr, the spatial error coefficient, in favor of the SLX specification, we still need to choose whether to use the numbers of housing units as weights for the zones, or not to do so (implicitly upweighting zones with relatively fewer housing units, and downweighting those with many). Table A.5 shows that the AIC values differ. Although AIC values give some guidance, and are based on log likelihood values that take account of the given weights, the choice between the two models depends on the analyst’s prior choice of weights. This suggests that Bayesian methods may well be relevant to permit better insight into this question in future research. If we take the 96 observation weighted SLX specification, the total impact of NOX is -0.02217 (standard error 0.005901), with equivalent values for the unweighted case: -0.03353 (standard error 0.005798). These values are substantially larger in absolute terms when compared with that found in Harrison, Rubinfeld (1978c, p. 100, coefficient -0.0064), and may reasonably be interpreted as indicating a substantially greater WTP for clean air than that found in the original study.
| OLS | SLX | SEM | SDEM | |
| TASSIM | 2118 | 6693 | 1866 | 6620 |
| TASSIM, weighted | 1157 | 4178 | 998 | 3999 |
| Census tracts | 1254 | 2223 | 520 | 1899 |
| Census tracts, weighted | 640 | 1240 | -150 | 929 |
Harrison, Rubinfeld (1978c, p. 87) use their estimation results to calculate a WTP value: “[W]hen NOX and the other values take on their mean values, the change in median housing values from a one pphm change in NOX is $1613”. Table 3 shows similar values, obtained by taking the difference between mean predictions for the 96 and 489 observation data sets, and both data sets with a one pphm reduction in NOX. Note that the result for the OLS 489 observation data set is $1254, less than the original result for 506 observations. Mean predictions are used instead of predictions from mean values to accommodate the spatially lagged independent variables included in the SLX and SDEM models. The WTP value for the weighted SLX model estimated using the TASSIM zones data set is $4178, under the same assumptions as those in the original research, but derived from a model now without serious mis-specification problems most likely related to the choice of observational units.
4 Concluding remarks
It has been demonstrated that the difficulties experienced in extracting a reasonable estimate of the air pollution coefficient from a model of the Boston house value data set that is not strongly mis-specified may be resolved by changing the unit of observation to that of the air pollution variable. Using TASSIM model output zones as the appropriate unit of observation does reduce the observation count and consequently increases the uncertainty of the coefficient expressed by its standard error, but also removes most of the mis-specification issues. In concluding, it will be suggested that this is not a one-off issue with this particular data set, but fits into discussion of the choice of units of observation in Regional Science.
In Complex spatial systems, Wilson (2000) distinguishes three dimensions which interact in urban and regional analysis: system articulation, theory, and method (see also Wilson 2002, 2012). System articulation is, in turn, made up of three sub-dimensions: entitation, levels of resolution (sectoral, spatial, temporal), and spatial representation. He argues that all too little attention is paid in analysis to careful planning of the main dimensions, with system articulation typically treated in the least satisfactory way. His second and third chapters provide a succinct and enlightening review of why system articulation matters — pointing back to Paelinck, Nijkamp (1975).
Both the spatial level of resolution and the mode of spatial representation are involved in spatial scale (see also Dray et al. 2012). Scale is intimately connected to the pattern/process matching that is central to analysis, because certain causal effects may be present only at particular scales. If the spatial representation (driven by available data) misses this scale, mis-specification issues may emerge (see also McMillen 2003). By using TASSIM zone units of observation, chosen to match the spatial pattern of entities corresponding to the TASSIM model output zones, and because these largely also correspond to the town units for which many other independent variables were measured, we have in this case removed the very high levels of autocorrelation induced by “copying out” to multiple census tracts belonging to these entities.
This is related to but probably not a case of the modifiable areal unit problem (Gelfand 2010); the observations in the case of the census tract data set are misaligned because of duplication of data observed for a smaller number of spatial entities covering the same geographical area (see also Haining 2010). This induces very strong spatial autocorrelation between proximate neighbors but does not add any information; it is also likely that heteroskedasticity is also induced by duplication. There is also a relationship to the ecological fallacy, in that the discussion in Harrison, Rubinfeld (1978c) largely relates to household WTP, but no household-level data is available. Wakefield, Lyons (2010) give a survey of the ecological fallacy in connection with spatial aggregation; the point of concern is the extension of aggregated inference to individuals within the aggregates.
In conclusion, researchers should be aware of the impact that choices of units of observation will have on the results that they obtain. Had Harrison, Rubinfeld (1978c) chosen to use TASSIM model output zones as units of observation, they would not only have avoided the serious mis-specification that has been subsequently found in their OLS model, but they would also have been able to establish that WTP for clean air was about three times higher than they believed at the time. Understanding how spatial data is organized has not been paid sufficient attention in spatial econometrics, often, as in this case, leading to spurious spatial autocorrelation stemming more from the way the data has been handled than from underlying data generation processes.
Acknowledgements
The author would like to thank the editors and two anonymous reviewers for their contributions to this article. Achim Zeileis, Antony Unwin, Tony Smith and Jon Wakefield kindly commented on the first version of the paper. Further helpful comments have been received during presentations at the Bergen Economics of Energy and Environment Research Conference, the Spatial Econometrics Association X World Conference, the R User Conference, a seminar at Adam Mickiewicz University, and from participants at graduate courses in the Universities of Innsbruck and Tartu, as well as during the Workshop in Honor of Manfred M. Fischer’s Retirement from his Professorship at WU Vienna. Remaining issues are entirely the responsibility of the author.
References
Anselin L, Lozano-Gracia N (2008) Errors in variables and spatial effects in hedonic house price models of ambient air quality. Empirical Economics 34: 5–34. CrossRef.
Belsley DA, Kuh E, Welsch RE (1980) Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. John Wiley & Sons, New York. CrossRef.
Dray S, Couteron P, Fortin MJ, Legendre P, Peres-Neto PR, Bellier E, Bivand R, Blanchet FG, de Cáceres M, Dufour AB, Heegaard E, Jombart T, Munoz F, Oksanen J, Pélissier R, Thioulouse J, Wagner HH (2012) Community ecology in the age of multivariate multiscale spatial analysis. Ecological Monographs 82: 257–275. CrossRef.
Drukker DM, Egger P, Prucha IR (2013) On two-step estimation of a spatial autoregressive model with autoregressive disturbances and endogenous regressors. Econometric Reviews 32: 686–733. CrossRef.
Gelfand AE (2010) Misaligned spatial data: The change of support problem. In: Gelfand AE, Diggle P, Guttorp P, Fuentes M (eds), Handbook of Spatial Statistics. Chapman & Hall/CRC, Boca Raton, 517–539. CrossRef.
Gibbons S, Overman HG (2012) Mostly pointless spatial econometrics? Journal of Regional Science 52: 172–191. CrossRef.
Gilley OW, Pace RK (1996) On the Harrison and Rubinfeld data. Journal of Environmental Economics and Management 31: 403–405. CrossRef.
Gotway CA, Young LJ (2002) Combining incompatible spatial data. Journal of the American Statistical Association 97: 632–648. CrossRef.
Haining RP (2010) The nature of georeferenced data. In: Fischer M, Getis A (eds), Handbook of Applied Spatial Analysis. Springer, Heidelberg, 197–217. CrossRef.
Halleck Vega S, Elhorst JP (2015) The SLX model. Journal of Regional Science 55: 339–363. CrossRef.
Harrison D, Rubinfeld DL (1978a) The air pollution and property value debate: Some empirical evidence. The Review of Economics and Statistics 60: 635–638. CrossRef.
Harrison D, Rubinfeld DL (1978b) Distribution of benefits from improvements in urban air-quality. Journal of Environmental Economics and Management 5: 313–332. CrossRef.
Harrison D, Rubinfeld DL (1978c) Hedonic housing prices and the demand for clean air. Journal of Environmental Economics and Management 5: 81–102. CrossRef.
Ingram GK, Fauth GR (1974) TASSIM: A Transportation and Air Shed SIMulation model, volume 1. case study of the Boston region. Department of City and Regional Planning, Harvard University
Ingram GK, Fauth GR, Kroch EA (1974) TASSIM: A Transportation and Air Shed SIMulation model, volume 2: program user’s guide. Department of City and Regional Planning, Harvard University
LeSage JP (2014) What regional scientists need to know about spatial econometrics. Review of Regional Studies 44: 13–32. CrossRef.
McMillen DP (2003) Spatial autocorrelation or model misspecification? International Regional Science Review 26: 208–217. CrossRef.
Ord J (1975) Estimation methods for models of spatial interaction. Journal of the American Statistical Association 70[349]: 120–126. CrossRef.
Pace RK, Gilley O (1997) Using the spatial configuration of the data to improve estimation. Journal of the Real Estate Finance and Economics 14: 333–340. CrossRef.
Pace RK, LeSage JP (2008) A spatial Hausman test. Economics Letters 101: 282–284. CrossRef.
Paelinck JHP, Nijkamp P (1975) Operational theory and method in regional economics. Saxon House, Farnborough
Piras G (2010) sphet: Spatial models with heteroskedastic innovations in R. Journal of Statistical Software 35: 1–21. CrossRef.
Solon G, Haider SJ, Wooldridge JM (2015) What are we weighting for? Journal of Human Resources 50: 301–316. CrossRef.
Wakefield JC, Lyons H (2010) Spatial aggregation and the ecological fallacy. In: Gelfand AE, Diggle P, Guttorp P, Fuentes M (eds), Handbook of Spatial Statistics. Chapman & Hall/CRC, Boca Raton, 541–558. CrossRef.
Waller LA, Gotway CA (2004) Applied Spatial Statistics for Public Health Data. John Wiley & Sons, Hoboken, NJ. CrossRef.
Wilson AG (2000) Complex spatial systems: The Modelling Foundations of Urban and Regional Analysis. Prentice Hall, Harlow. CrossRef.
Wilson AG (2002) Complex spatial systems: Challenges for modellers. Mathematical and Computer Modelling 36: 379–387. CrossRef.
Wilson AG (2012) The science of cities and regions: lectures on mathematical model design. Springer, Dordrecht. CrossRef.
Wong D (2010) The modifiable areal unit problem (MAUP). In: Fotheringham AS, Rogerson PA (eds), The SAGE Handbook of Spatial Analysis. SAGE Publications Ltd, London, 105–123. CrossRef.
A Appended figures and tables
| minimum | lower | median | upper | maximum | |
| quartile | quartile | ||||
| Block housing unit counts by tract | 151.00 | 1174.50 | 1610.00 | 2165.00 | 5482.00
|
| Block counts by tract | 1.00 | 26.00 | 47.50 | 70.00 | 299.00
|
| Block housing unit counts | -1.00 | 10.00 | 19.00 | 37.00 | 1564.00
|
| Min. | Median | Mean | Max. | |
| units | 5.00 | 526.00 | 690.10 | 3031.00 |
| log(median) | 8.63 | 9.95 | 9.92 | 10.82 |
| CRIM | 0.01 | 0.25 | 3.45 | 88.98 |
| ZN | 0.00 | 0.00 | 11.13 | 100.00 |
| INDUS | 0.74 | 9.69 | 11.10 | 27.74 |
| CHAS | 0.00 | 0.00 | 0.06 | 1.00 |
| I((NOX * 10)^2) | 14.82 | 28.94 | 32.04 | 75.86 |
| I(RM^2) | 12.68 | 38.35 | 39.46 | 77.09 |
| AGE | 2.90 | 76.70 | 68.21 | 100.00 |
| log(DIS) | 0.13 | 1.19 | 1.20 | 2.50 |
| log(RAD) | 0.00 | 1.61 | 1.86 | 3.18 |
| TAX | 187.00 | 330.00 | 407.50 | 711.00 |
| PTRATIO | 12.60 | 19.10 | 18.52 | 22.00 |
| I(BB/100) | 0.00 | 0.01 | 0.06 | 0.96 |
| log(I(LSTAT/100)) | -3.92 | -2.15 | -2.21 | -0.97 |
| Min. | Median | Mean | Max. | |
| units | 25.00 | 2926.00 | 3588.00 | 12410.00 |
| log(median) | 9.12 | 9.82 | 9.83 | 10.56 |
| CRIM | 0.01 | 0.08 | 1.96 | 18.13 |
| ZN | 0.00 | 0.00 | 25.89 | 100.00 |
| INDUS | 0.46 | 6.01 | 8.55 | 27.74 |
| CHAS | -1.00 | -1.00 | -0.85 | 0.00 |
| I((NOX * 10)^2) | 14.82 | 21.76 | 26.68 | 75.86 |
| I(RM^2) | 25.93 | 39.60 | 41.82 | 62.77 |
| AGE | 8.97 | 51.76 | 56.02 | 100.00 |
| log(DIS) | 0.14 | 1.54 | 1.42 | 2.50 |
| log(RAD) | 0.00 | 1.61 | 1.62 | 3.18 |
| TAX | 187.00 | 307.00 | 376.20 | 711.00 |
| PTRATIO | 12.60 | 18.25 | 17.93 | 22.00 |
| I(BB/100) | 0.00 | 0.01 | 0.04 | 0.78 |
| log(I(LSTAT/100)) | -3.52 | -2.46 | -2.42 | -1.43 |
| OLS | SLX | SEM | SDEM | |
| Census tracts | -318.53 | -405.93 | -515.03 | -563.15 |
| Census tracts with weights | -512.77 | -566.90 | -684.34 | -700.45 |
| OLS | SLX | SEM | SDEM | |
| TASSIM zones | -95.68 | -135.50 | -97.20 | -133.57 |
| TASSIM zones with weights | -135.25 | -151.84 | -144.19 | -150.04 |
| BP test | p-value | BP test | p-value | |
| with units | ||||
| TASSIM zones OLS | 51.429 | 1.6921e-06 | 4.942 | 0.02621 |
| TASSIM zones SLX | 29.901 | 0.27173 | 3.859 | 0.04949 |
| Census tracts OLS | 83.133 | 2.8297e-12 | 22.24 | 2.410e-06 |
| Census tracts SLX | 100.87 | 9.1962e-11 | 20.36 | 6.424e-06 |
| TASSIM zones | p-value | Census tracts | p-value | |
| OLS | 2.1767 | 0.01475 | 15.997 | < 2.2e-16 |
| Weighted OLS | 4.3071 | 8.271e-06 | 13.901 | < 2.2e-16 |
| SLX | 1.5739 | 0.05776 | 15.413 | < 2.2e-16 |
| Weighted SLX | 1.9261 | 0.02704 | 13.21 | < 2.2e-16 |
| Robust LM error | p-value | Robust LM lag | p-value | |
| TASSIM zones OLS | 0.10147 | 0.7501 | 5.0123 | 0.0251675 |
| TASSIM zones SLX | 0.093408 | 0.7599 | 0.05813 | 0.8094769 |
| Census tracts OLS | 234.4 | <2e-16 | 11.362 | 0.0007496 |
| Census tracts SLX | 177.56 | <2e-16 | 0.10978 | 0.7404000 |
| TASSIM zones | p-value | Census tracts | p-value | |
| SEM | 31.113 | 0.005345 | 52.192 | 2.609e-06 |
| Weighted SEM | 19.027 | 0.163938 | 26.567 | 0.021907 |
| SDEM | 17.712 | 0.912070 | 53.272 | 0.001866 |
| Weighted SDEM | 19.199 | 0.862621 | 48.936 | 0.006024 |
| TASSIM zones | p-value | Census tracts | p-value | |
| SEM | 0.40436 | 0.001271 | 0.73273 | < 2.2e-16 |
| Weighted SEM | 0.46709 | 7.566e-05 | 0.69576 | < 2.2e-16 |
| SDEM | 0.056156 | 0.717637 | 0.65797 | < 2.2e-16 |
| Weighted SDEM | 0.09641 | 0.528010 | 0.62017 | < 2.2e-16 |
| Model type | Direct | Indirect | Total | WTP |
| TASSIM ZONE:NO WEIGHTS:OLS | -0.011799 | -0.011799 | 2118 | |
| (0.00269) | (0.00269) | |||
| TASSIM ZONE:WEIGHTS:OLS | -0.0067082 | -0.0067082 | 1157 | |
| (0.002654) | (0.002654) | |||
| TASSIM ZONE:NO WEIGHTS:SEM | -0.010464 | -0.010464 | 1866 | |
| (0.002909) | (0.002909) | |||
| TASSIM ZONE:WEIGHTS:SEM | -0.0058313 | -0.0058313 | 998 | |
| (0.002906) | (0.002906) | |||
| CENSUS TRACT:NO WEIGHTS:OLS | -0.0059344 | -0.0059344 | 1254 | |
| (0.001074) | (0.001074) | |||
| CENSUS TRACT:WEIGHTS:OLS | -0.0030698 | -0.0030698 | 640 | |
| (0.001126) | (0.001126) | |||
| CENSUS TRACT:NO WEIGHTS:SEM | -0.0024688 | -0.0024688 | 520 | |
| (0.001528) | (0.001528) | |||
| CENSUS TRACT:WEIGHTS:SEM | 0.00071832 | 0.00071832 | -150 | |
| (0.00155) | (0.00155) | |||
| TASSIM ZONE:NO WEIGHTS:SLX | -0.013772 | -0.019762 | -0.033534 | 6693 |
| (0.002337) | (0.005609) | (0.005798) | ||
| TASSIM ZONE:WEIGHTS:SLX | -0.010402 | -0.011771 | -0.022173 | 4178 |
| (0.002986) | (0.005925) | (0.005901) | ||
| TASSIM ZONE:NO WEIGHTS:SDEM | -0.013755 | -0.01947 | -0.033225 | 6620 |
| (0.003242) | (0.007836) | (0.008189) | ||
| TASSIM ZONE:WEIGHTS:SDEM | -0.010231 | -0.011097 | -0.021328 | 3999 |
| (0.004118) | (0.008241) | (0.008419) | ||
| CENSUS TRACT:NO WEIGHTS:SLX | 0.0027696 | -0.01308 | -0.010311 | 2223 |
| (0.002079) | (0.002461) | (0.001208) | ||
| CENSUS TRACT:WEIGHTS:SLX | 0.0038597 | -0.0097492 | -0.0058895 | 1240 |
| (0.002098) | (0.002468) | (0.001319) | ||
| CENSUS TRACT:NO WEIGHTS:SDEM | 0.0010074 | -0.0099152 | -0.0089077 | 1899 |
| (0.001682) | (0.002529) | (0.002239) | ||
| CENSUS TRACT:WEIGHTS:SDEM | 0.0030491 | -0.0075263 | -0.0044772 | 929 |
| (0.00173) | (0.002639) | (0.002469) | ||
