 Volume
5, Number 3, 2018, R13–R18 journal homepage:
region.ersa.org
Volume
5, Number 3, 2018, R13–R18 journal homepage:
region.ersa.orgDOI: 10.18335/region.v5i3.254
A Short Course on Spatial Econometrics and GIS
1 North Carolina A&T State University, Greensboro, NC, USA Received: 20 August 2018/Accepted: 26 August 2018Abstract. This resource gives a brief overview of a website and playlist of YouTube videos using open source software (R, GeoDa, and QGIS) designed to help get scholars up and running with analyzing their own data using Spatial Econometrics. Sample data, handouts, code, and map files are provided for ease of replication. The course covers the basics of integrating data into a spatial data set, contiguity and spatial correlation, doing basic spatial regressions in GeoDa, and doing more sophisticated specification tests and regressions in R.
JEL classification: R1, C21
Key words: spatial econometrics, instructional videos
1 Introduction
The internet has drastically improved the ability to provide quality distance-learning opportunities over the past decade. The explosion of MOOCs and high-quality educational videos hosted on YouTube have reduced the need for professionals to travel to a certain place in order to learn or refresh their skills in mathematics or data analysis. While there are still many opportunities for taking these courses at various conferences or universities, there are cheaper high quality substitutes becoming available. Specifically when it comes to Spatial Econometrics, there are many opportunities to travel for face-to-face instruction (Table 1), and the author of this article benefitted greatly from a short course offered by Luc Anselin at UI-UC in 2003. However, these courses can easily cost well over $5,000 when the tuition, travel, and lodging are factored in. In this paper we introduce one complete, yet continuing series of free resources that are available.
| Location | Recent Offerings | Cost |
| Regional Research Institute, | Summer, 1 Week, | $3,000 + lodging, |
| West Virginia University, USA | 2016-2019 | travel (2018) |
| Spatial Econometrics Advanced | Summer, 4 weeks, | € 2,300-3,300 + lodging, |
| Institute, Università Cattolica | 2018 | travel (2018) |
| del Sacro Cuore of Rome | ||
| ICPSR, University of Michigan, | Summer, 1 Week | $1,700-3,200 + lodging, |
| USA | travel (2018) | |
| NARSC Workshop, San Anto- | 1 Day, before the | $95 in addition to the |
| nio, TX, USA | start of the 2018 | cost of attending |
| NARSC Conference | NARSC Conference | |
2 Overview of the course
The core of the course is comprised of 12 YouTube videos, between 15 and 41 minutes long. These videos use screen capture technology (Burkey 2015), rather than videos of a professor in front of a typical classroom. All of the videos and materials are free of charge, posted at http://spatial.burkeyacademy.com. The software used is also all freely available1 , making the course very accessible to faculty and students alike. Each video has an accompanying handout, dataset, Excel file, or text file containing code, as is appropriate.
3 Brief outline of the course
Though additions to the series will continue to be made based on viewer feedback, the core 12 videos (plus an additional 9-minute brief “Welcome” video) form a complete, though basic introduction to Spatial Econometrics. It is assumed that the viewers are familiar with cross-sectional econometrics and basic matrix notation. Some basic familiarity with map files and R would be helpful, but not required.
3.1 Introduction to thinking spatially with some econometric models
The first video outlines some of the major Spatial Econometric Models and how to think about spatial interaction/spillover in basic terms. The video and handout also discuss some of the major researchers who developed the models, and give some references for books and journal articles where viewers can find more information. In this section we introduce the following models:
OLS Model
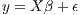 | (1) |
The OLS model does not contain a spatial relationship, but is often used as a starting place. Anselin (1988) favored the Lagrange Multiplier approach to specification searches. Starting with OLS, Anselin derived 5 Lagrange Multiplier statistics that help determine if the (possibly misspecified) OLS model points toward the Spatial Lag, Spatial Error, or SARMA models, though he suggested that the SARMA model was probably never the correct specification.
Measuring “neighbors” with a Spatial Weights Matrix, W, allows us to mathematically specify how spatial relationships among regions might be structured. Regions might be related with their neighbors in three different ways:
- 1.
- The value of y in a region might impact (or be related to) the value of y in a neighboring region
- 2.
- The values of X’s in a region might affect (or be related to) the value of y in a neighboring region
- 3.
- The residuals ϵ might affect (or be related to) the residuals in a neighboring region (spatial heteroskedasticity or spatial autocorrelation)
Manski Model
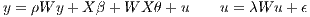 | (2) |
The Manski Model builds in all three types of spatial relationship. If θ = 0 then Manski becomes the Kelejian-Prucha Model:
Kelejian-Prucha, SARAR, Cliff-Ord, SAC model
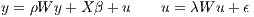 | (3) |
Or if λ = 0, we get the Spatial Durbin Model (SDM), which involves lagged y and spatially-related residuals. LeSage, Pace (2009) favor starting with this specification (or the Spatial Durbin Error Model, discussed in the last of the core videos), and then using Likelihood Ratio techniques to test to see if the model should be restricted to a simpler, nested model.
Spatial Durbin Model
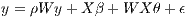 | (4) |
If ρ = 0, then this becomes the
Spatially Lagged X (SLX) Model
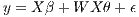 | (5) |
If θ = 0, then (4) degenerates into the Spatial Lag Model
Spatial Lag, Spatial Autoregressive (SAR)
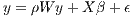 | (6) |
If θ = -ρβ, then (4) simplifies into the spatial error model (because λ = ρ in this case)2 .
![y = ρW y+ X β +W X[θ = - ρβ]+ ϵ
y = ρW [X β + ϵ]+ X β + W X[- ρβ ]+ ϵ
y = ρW X β + ρW ϵ+ X β + W X[- ρβ ]+ ϵ](25411x.png)
Spatial Error (SEM)
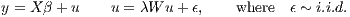 | (7) |
Of course, setting all of the spatial parameters (λ, ρ, and the vector of θ’s) to zero will restrict the model back to OLS.
3.2 GIS basics
The next two videos give a brief introduction to using QGIS (QGIS Development Team 2018). The focus is on how to download a SHP file mapping a set of regions, open it in a GIS program, edit it by removing regions that may not be of interest, and add additional data for the regions to be analyzed. Users are provided with a ZIP file to download that contains the map files and extra data to import for practice with the video.
3.3 Understanding the idea of contiguity and spatial correlation
A video focusing on contiguity and spatial correlation (Moran’s I) follows, along with a downloadable spreadsheet file. In this file the viewers help to complete small contiguity and weights matrices by hand, using a simple set of regions. The users are shown how simple row standardization can be done. This spreadsheet allows users to change data values in each region, and dynamically see how the value of the spatial correlation changes as the user creates different patterns in the data.
3.4 ESDA, making and visualizing spatial weights for spatial data with GeoDa
The next four videos in the series use GeoDa’s fantastic visualization tools (Anselin et al. 2006) to do basic Exploratory Spatial Data Analysis (ESDA), create and export spatial weights matrices, calculate spatial correlations, and do basic spatial regressions and specification tests. The strengths and weaknesses of GeoDa are discussed, and the user is encouraged to also learn R for spatial data analysis in the remaining videos.
3.5 R for spatial data analysis and regression
In the final four videos of the sequence, the user is introduced to R, and many of the common packages used for spatial data manipulation and analysis (especially spdep (Bivand, Piras 2015, Bivand et al. 2013). The first two videos focus on getting data into R and creating contiguity matrices. Viewers are shown how to read in spatial data, create weights matrices, import weights created in GeoDa, export weights, and plot contiguity relationships.
The final two videos in the core of the series explore ways to perform a spatial specification search and estimate many of the common spatial econometric models in R. The difference between Lagrange Multiplier (LM) tests and Likelihood Ratio (LR) tests are discussed. In summary, the LM tests begin with estimating a nonspatial OLS model and calculating the score, indicating the rate of improvement in the model fit as we relax the constraints making the model nonspatial. Anselin derived five LM tests: One for the SEM and SAR (with a robust version for these, attempting to filter out some propensity for a false positive between these two models), and a test for a SARMA Model3 .
The benefit to the LM approach is that only the OLS model needs to be estimated before calculating the LM statistics. However, this method of spatial specification search is very limiting, because only three types of models can be considered. Thus, many spatial econometricians favor the LR approach, because any model can be tested to see if a simpler, nested model may be more appropriate (See Figure 1). The LR statistic is also very easy to calculate after running the two models to be compared:
| LRstat = | - 2(Lrestricted - Lunrestricted) ~ χ2(# restrictions) | (8) | |
| Ho: restricted model is true |
LeSage (2014) suggests running the SDM if a global specification is needed, and if a local structure is needed, first run the Spatial Durbin Error Model (SDEM):
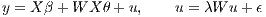 | (9) |
This model is “local” because it does not contain a lag y term; so while neighbors affect each other, this effect does not propagate throughout the entire space. Links to the data, commands, and handouts are included, along with a two-page spatial econometrics in R reference sheet with commands and tips (Figure 2).
4 Conclusion
While this web page and YouTube series are not a perfect substitute for a short course, it is hoped that it helps to introduce Spatial Econometrics to a wider audience, and serve as a resource for those who cannot afford to take a face to face course. The author welcomes any suggestions and corrections from the academic community. The author hopes to add some interviews with leading researchers in the field to this series of videos, as well as add additional topics of interest.
Acknowledgement
Thanks to Stephanie Kelly for editorial assistance.
References
Anselin L (1988) Spatial Econometrics: Methods and Models. Kluwer Academic Publishers, Dordrecht. CrossRef.
Anselin L, Syabri I, Kho Y (2006) Geoda: An introduction to spatial data analysis. Geographical Analysis 38[1]: 5–22. CrossRef.
Bivand RS, Hauke J, Kossowski T (2013) Computing the Jacobian in Gaussian spatial autoregressive models: An illustrated comparison of available methods. Geographical Analysis 45[2]: 150–179. CrossRef.
Bivand RS, Piras G (2015) Comparing implementations of estimation methods for spatial econometrics. Journal of Statistical Software 63[18]: 1–36. CrossRef.
Burkey ML (2015) Making educational and scholarly videos with screen capture software. REGION 2[2]: R2–10. CrossRef.
Burkey ML (2018) The mother of all R spatial econometrics handouts. Available from http://spatial.burkeyacademy.com
LeSage JP (2014) What regional scientists need to know about spatial econometrics. The Review of Regional Studies 44[1]: 13–32
LeSage JP, Pace RK (2009) Introduction to Spatial Econometrics. CRC Press, Boca Raton, FL. CrossRef.
QGIS Development Team (2018) QGIS geographic information system. Open source geospatial foundation project. http://qgis.osgeo.org
A list of the videos with descriptions and links to the supplementary material can be found at http://spatial.burkeyacademy.com.
The playlist of videos is at https://www.youtube.com/playlist?list=PLlnEW8MeJ4z6Du_cbY6o08KsU6hNDkt4k
 © 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
© 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)


