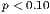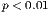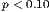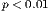Volume
1, Number 1, 2014, 25-65 journal homepage:
region.ersa.org
Volume
1, Number 1, 2014, 25-65 journal homepage:
region.ersa.orgInfrastructure and Trade: A Meta-Analysis*
1 UNU-MERIT, Maastricht Graduate School of Governance, Maastricht University, Maastricht, The Netherlands. E-mail: celbis@merit.unu.edu2 Department of Spatial Economics, Free University of Amsterdam, Amsterdam, The Netherlands. E-mail: p.nijkamp@vu.nl
3 National Institute of Demographic and Economic Analysis, University of Waikato, Hamilton, New Zealand. E-mail: jpoot@waikato.nz Received: 16 July 2014/Accepted: 17 December 2014
*The authors would like to thank the audience at the following paper presentations for valuable comments and discussions: 9th World Congress of Regional Science Association International; Timisoara, Romania, May 9-11, 2012; 12th PRSCO Summer Institute and the 4th International Conference of RSAI on Regional Science and Sustainable Regional Development, Renmin University, Beijing, China, July 3-6, 2012; Meta-analysis in Economics Research Network (MAER-Net) Colloquium, Edith Cowan University, Perth, Australia, September 18-20, 2012; New Zealand Productivity Commission, Wellington, New Zealand, September 28, 2012; Tinbergen Institute, Amsterdam, The Netherlands, November 26, 2012; Economics Department, University of Canterbury, Christchurch, New Zealand, May 24, 2013. Another version of this manuscript is also available online as a UNU-MERIT working paper with serial number 2013-032.
Abstract. Low levels of infrastructure quality and quantity can create trade impediments through increased transport costs. Since the late 1990s, an increasing number of trade studies have taken infrastructure into account. The purpose of the present paper is to quantify the importance of infrastructure for trade by means of meta-analysis and meta-regression techniques that synthesize various studies. The type of infrastructure that we focus on is mainly public infrastructure in transportation and communication. We examine the impact of infrastructure on trade by means of estimates obtained from 36 primary studies that yielded 542 infrastructure elasticities of trade. We explicitly take into account that infrastructure can be measured in various ways and that its impact depends on the location of the infrastructure. We estimate several meta-regression models that control for observed heterogeneity in terms of variation across different methodologies, infrastructure types, geographical areas and their economic features, model specifications, and publication characteristics. Additionally, random effects account for between-study unspecified heterogeneity, while publication bias is explicitly addressed by means of the Hedges model. After controlling for these issues, we find that a 1 percent increase in own infrastructure increases exports by about 0.6 percent and imports by about 0.3 percent. Such elasticities are generally larger for developing countries, land infrastructure, IV or panel data estimation, and macro-level analyses. They also depend on the inclusion or exclusion of various common covariates in trade regressions.
JEL classification: F10, H54, R53, C10, F1, R4
Key words: Infrastructure, Trade, Transportation, Communication, Public Capital, Meta-Analysis
1 Introduction
The export-led growth hypothesis,1 and the underlying reasons of persistent trade deficits have been well researched and debated by academics and policymakers. Within the context of free trade, ways to increase competitiveness other than through exchange rate interventions, tariffs, and quotas have been attracting interest. The reduction of transport costs is arguably the most emphasized such method. Formally, transport costs are seen as a determining factor of trade flows in the gravity model of trade. Regarding this relationship between transport costs and trade, Volpe Martincus et al. (2014, 149) state “the extent to which these costs matter is, however, far less well-established.” As a result, with respect to transport costs, the effects of trade-related infrastructure on trade flows have increasingly become a focal point in studies examining the trade performance of countries and regions in recent years.
The present study uses meta-analysis and meta-regression techniques to synthesize various “quantitative opinions” (Poot 2014) that can be found in the trade literature. The type of infrastructure that we focus on is mainly public infrastructure in transportation and communication. Our meta-analysis has several attributes. First, because all estimated effects are in the form of comparable elasticities, we can calculate precision-weighted averages of the likely impact of a given percentage increase in transportation infrastructure, broadly interpreted, on a country’s trade. Second, we show that this likely impact is larger in developing countries and is expected to be trade balance-enhancing. Third, we show how such weighted average estimates from the literature are linked to a wide range of study features. Fourth, the systematic analysis of all studies conducted to date can provide a platform for designing new primary studies. Fifth, our meta-regression analysis is more transparent and replicable than a conventional narrative literature review. The data used in this study and the Stata code can be downloaded from http://merit.unu.edu/staff/celbis/.
Infrastructure is a multidimensional concept that is measured in various ways: both in relation to trade performance, and in estimating its impact on growth, welfare, efficiency, and other types of economic outcomes. As will be seen in our literature survey, empirical research often defines infrastructure as a portfolio of components, meaningful only in an integrated sense. Consequently, a wide range of approaches exists in the literature regarding the conceptualization and classification of infrastructure. Martin, Rogers (1995, 336) define public infrastructure as “any facility, good, or institution provided by the state which facilitates the juncture between production and consumption. Under this interpretation, not only transport and telecommunications but also such things as law and order qualify as public infrastructure.” In this study, we focus exclusively on models that estimate the impacts of indicators of transportation and communication infrastructure. Recognizing the “collective” nature of infrastructure, we pay specific attention to variation in effect size in terms of the way in which infrastructure is measured in the primary studies. Nonetheless, the remaining types of public infrastructure such as rule of law, regulatory quality, etc. are to some extent considered by controlling for such attributes in the meta-regression models employed in this study.
We collected a large number of research articles that use regression analysis with at least one transportation and/or communication infrastructure-related factor among the explanatory variables, and a dependent variable that represents either export or import volumes or sales. These papers have been collected by means of academic search engines and citation tracking. Our search yielded 36 articles published between 1999 and 2012, which provided sufficiently compatible information for meta-analytical methods. These papers are broadly representative of the literature in this area. Section 5 describes the selection of primary studies and coding of data.
The rest of this paper is structured as follows: Section 2 provides a short narrative literature survey. The theoretical model that underlies most regression models of merchandise trade flows and the implications for meta-regression modeling are outlined in Section 3. The meta-analytic methodology is briefly described in Section 4. The data are discussed in Section 5, which is followed by descriptive analysis in Section 6, and meta-regression modeling in Section 7. Section 8 presents some final remarks.
2 Literature review
The broad literature on infrastructure and trade provides certain stylized facts: the relative locations of trade partners and the positioning of infrastructure, together with the trajectories of trade, can be seen as integral features that play a role in the relationship between infrastructure and trade flows. The location of physical infrastructure and the direction of trade strongly imply a spatial dimension to the relationship and can be subject to various costs that are closely linked with space, infrastructure quality, and availability. Thus, the relationship in question is usually assessed in relation to space and trade costs. For instance, Donaghy (2009, 66) states that “trade, international or interregional, is essentially the exchange of goods and services over space. By definition, then, it involves transportation and, hence, some transaction costs.” The history of the analysis of transport cost impacts on starts with von Thünen (1826), and is later elaborated by Samuelson (1952, 1954), Mundell (1957), Geraci, Prewo (1977), Casas (1983), Bergstrand (1985) and others. Recently, the specific role of infrastructure in trade has been attracting increasing attention. The relationship has become more prominent in the trade literature, especially after seminal studies such as Bougheas et al. (1999) and Limao, Venables (2001), who empirically demonstrate that infrastructure plays an important role in determining transport costs.
Nevertheless, pinpointing the exact impact of infrastructure on trade remains a challenge. The range of estimates found in the literature is wide. This may be due to numerous factors such as the relevant geographical characteristics, interrelations of different infrastructure types, infrastructure capacity utilization, and study characteristics. Additionally there are challenges in the ways in which infrastructure is defined. Bouet et al. (2008, 2) draw attention to this by stating:
Quantifying the true impact of infrastructure on trade however is difficult mainly because of the interactive nature of different types of infrastructure. Thus, the impact of greater telephone connectivity depends upon the supporting road infrastructure and vice versa. Most importantly, the precise way this dependence among infrastructure types occurs is unknown and there does not exist any a priori theoretical basis for presuming the functional forms for such interactions.
Thus, the infrastructure effects may be non-linear and may need to be explored by taking account of the interactions of different infrastructure types. Additionally, Portugal-Perez, Wilson (2012) draw attention to the possibility of infrastructure satiation in their results from a sample of 101 countries. They find that the impact of infrastructure enhancements on export performance is decreasing in per capita income while information and communication technology is increasingly influential for wealthier countries, implying diminishing returns to transport infrastructure.
Another question that arises in assessing the impact of infrastructure on trade is the asymmetry in the impact of infrastructure in the two directions of bilateral trade. In this regard, Martinez-Zarzoso, Nowak-Lehmann (2003) examine the EU-Mercosur bilateral trade flows and conclude that investing in a trade partner’s infrastructure is not beneficial because only the exporter’s infrastructure enhances trade. This result is not universal, however. Limao, Venables (2001) consider importer, exporter, and transit countries’ levels of infrastructure separately and conclude that each of these dimensions of infrastructure positively affect bilateral trade flows. Similarly, Grigoriou (2007) concludes that – based on results obtained from a sample of 167 countries – road construction within a landlocked country may not be adequate to enhance trade because transit country infrastructure, bargaining power with transit countries, and transport costs also play important roles in trade performance.
Additionally, the impact of infrastructure may not be symmetric for trade partners who have different economic characteristics. For example, Longo, Sekkat (2004) find that both exporter and importer infrastructure play a significant role in intra-African trade. These authors do not, however, find a significant infrastructure impact regarding trade flows between Africa and major developed economies. In another study on intra-African trade, Njinkeu et al. (2008) conclude that port and services infrastructure enhancement seem to be a more useful tool in improving trade in this region than other measures.
Another issue is that infrastructure specific to one geographical part of an economy may affect exports or imports at another location within the same economy. If the two locations are relatively far apart, this may yield unreliable results when broad regions are the spatial unit of measurement. Smaller spatial units of analysis may then be beneficial; however, subnational-level studies on the impact of infrastructure on trade are relatively rare. Wu (2007) provides evidence from Chinese regions and finds a positive impact of infrastructure (measured as total length of highways per square kilometer of regional area) on export performance. Similarly, in another sub-national level study, Granato (2008) examines the export performance of Argentinean regions to 23 partner countries. The author finds that transport costs and regional infrastructure are important determinants of regional export performance.
In the trade literature, infrastructure is usually measured in terms of stock or density, or by constructing a composite index using data on different infrastructure types. Adopting a broad view of infrastructure, Biehl (1986) distinguishes the following infrastructure categories: transportation, communication, energy supply, water supply, environment, education, health, special urban amenities, sports and tourist facilities, social amenities, cultural amenities, and natural environment. The transportation category can be classified into subcategories such as roads, railroads, waterways, airports, harbors, information transmission, and pipelines (Bruinsma et al. 1989). Nijkamp (1986) identifies the features that distinguish infrastructure from other regional potentiality factors (such as natural resource availability, locational conditions, sectoral composition, international linkages and existing capital stock) as high degrees of: publicness, spatial immobility, indivisibility, non-substitutability, and monovalence. Based on the methods employed in the primary studies, we distinguish two main approaches regarding the measurement of infrastructure: the usage of variables measuring specific infrastructure types, and/or employing infrastructure indexes. This point is further elaborated in Section 5.
3 The theory of modeling trade flows
An improvement in infrastructure is expected to lower the trade hindering impact of transport costs. Transport costs have a negative impact on trade volumes as trade takes place over space, which incurs costs in moving products from one point to another. Such costs may include fuel consumption, tariffs, rental rates of transport equipment, public infrastructure tolls, and time costs. A convenient way to represent such costs is the “iceberg melting” model of Samuelson (1954) in which only fractions of goods that are shipped arrive at their destination. In this regard, Fujita et al. (1999) refer to von Thünen’s example of trade costs where a portion of grain that is transported is consumed by the horses that pull the grain wagon. Fujita et al. (1999) model the role of such trade costs in a world with a finite number of discrete locations where each variety of a product is produced in only one location and all varieties produced within a location have the same technology and price. The authors show that the total sales of a variety particular to a specific region depends – besides factors such as the income levels in each destination and the supply price – on the transportation costs to all destinations.
Anderson, van Wincoop (2003) show that bilateral trade flows between two spatial trading units depend on the trade barriers that exist between these two traders and all their other trade partners. The authors start with maximizing the CES utility function:
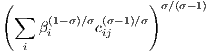 | (1) |
with substitution elasticity σ > 1 and subject to the budget constraint
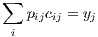 | (2) |
where subscripts i and j refer to regions and each region is specialized in producing only one good. cij is the consumption of the goods from region i by the consumers in region j, βi is a positive distribution parameter, and yj is the size of the economy of region j in terms of its nominal income. pij is the cost, insurance and freight (cif) price of the goods from region i for the consumers in region j and is equal to pitij where pi is the price of the goods of region i in the origin (supply price) and tij is the trade cost factor between the origin i and the destination j, and pij cij = xij is the nominal value of exports from i to j. The income of region i is the sum of the values of all exports of i to the other regions:
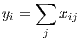 | (3) |
Maximizing (1) subject to (2), imposing the market clearing condition (3), and assuming that tij = tji (i.e. trade barriers are symmetric) leads to the gravity equation:
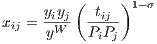 | (4) |
where yW ≡∑ jyj is the world nominal income. Anderson, van Wincoop (2003, 2004) refer to Pi and Pj as “multilateral resistance” variables which are defined as follows:
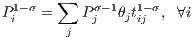 | (5) |
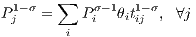 | (6) |
in which θ is the share of region j in world income, 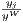 . Therefore, the authors show in
equations (5) and (6) that the multilateral resistance terms depend on the bilateral trade
barriers between all trade partners. Moreover, the gravity equation (4) implies that the trade
between i and j depends on their bilateral trade barriers relative to the average trade barriers
between these economies and all their trading partners. Anderson, van Wincoop (2003)
finalize their development of the above gravity model by defining the trade cost factor
as a function of bilateral distance (dij) and the presence of international borders.
Here, tij = bijdijρ; where if an international border between i and j does not exist
bij = 1, otherwise it is one plus the tariff rate that applies to that specific border
crossing.
. Therefore, the authors show in
equations (5) and (6) that the multilateral resistance terms depend on the bilateral trade
barriers between all trade partners. Moreover, the gravity equation (4) implies that the trade
between i and j depends on their bilateral trade barriers relative to the average trade barriers
between these economies and all their trading partners. Anderson, van Wincoop (2003)
finalize their development of the above gravity model by defining the trade cost factor
as a function of bilateral distance (dij) and the presence of international borders.
Here, tij = bijdijρ; where if an international border between i and j does not exist
bij = 1, otherwise it is one plus the tariff rate that applies to that specific border
crossing.
Infrastructures can be interpreted as the facilities and systems that influence the effective bilateral distance, dij. Lower levels of infrastructural quality can increase transportation costs. Examples of this are increased shipping costs in a port when there is congestion due to insufficient space; higher fuel consumption due to low quality roads; and more time spent in transit because of shortcomings in various types of facilities. Within the context of the iceberg melting model mentioned earlier, Bougheas et al. (1999) construct a theoretical framework in which better infrastructure increases the fraction that reaches the destination through the reduction of transport costs. By including infrastructure variables in their empirical estimation using a sample of European countries, the authors find a positive relationship between trade volume and the combined level of infrastructure of the trading partners. Many other studies on bilateral trade flows have constructed specific functional forms of the bilateral trade barriers (trade costs) that take the level of infrastructure into account.
An important assumption in the derivation of the gravity model presented in equation (4) is that tij = tji, which leads to xij = xji (balanced bilateral trade). In practice, every trade flow is directional and infrastructure conditions at the origin of trade (the exporting country) may impact the trade flow differently than conditions at the destination of trade (the importing country). Defining ki (kj) as the infrastructure located in origin i (destination j), referred to in the remainder of the paper as “exporter infrastructure” and “importer infrastructure”, this implies that ∂dij∕∂ki≠∂dij∕∂kj. At the same time, there are two ways to empirically measure the trade flow: as export at the point of origin or as import at the point of destination. This implies that from the perspective of any given country i, there are in principle four ways of measuring the impact of infrastructure on trade:
- The impact of ki on xij (own country infrastructure on own exports)
- The impact of ki on xji (own country infrastructure on own imports)
- The impact of kj on xij (partner country infrastructure on own exports)
- The impact of kj on xji (partner country infrastructure on own imports)
Logically, with a square trade matrix, i and j, can be chosen arbitrarily and the impact of ki on xij must therefore be the same as the impact of kj on xji (and the impact of ki on xji the same as the impact of kj on xij). Thus, in a cross-section setting, a regression of world trade on infrastructure gives only two effect sizes in theory. Such a regression equation, when estimated with bilateral trade data, may look like: ln(xij) = a + boln(ki) + bdln(kj) + othervars + eij where a is a constant term, bo is the origin infrastructure elasticity of trade (exporter infrastructure), bd is the destination infrastructure elasticity of trade (importer infrastructure) and eij is the error term. With n countries, i = 1,...,n and j = 1,...,n - 1 and the number of regression observations is n(n - 1).
An issue that arises in practice is that regressions may yield different results when estimated with export data as compared with import data. In other words, referring to box and bdx as bo and bd estimated with export data (and bom and bdm similarly defined with import data); in theory box = bom and bdx = bdm, but we shall see that in our meta-regression analysis box > bom, while bdx < bdm. This simply means that a larger estimate is obtained when the trade flow is defined from the perspective of the country where the infrastructure is located rather than from the perspective of the partner country. Hence, producer/exporter country infrastructure has a bigger effect when measured with export data, while consumer/importer country infrastructure has a bigger effect when measured with import data.
4 Methodology
Meta-analysis of empirical research, first defined by Glass (1976) as “the analysis of analyses” has been a common method in experimental research such as medicine and psychology since the early 20th century and has gained popularity in economic research in recent decades (Poot 2014, Ridhwan et al. 2010). Stanley, Jarrell (1989, 301) state “meta-analysis is the analysis of empirical analyses that attempts to integrate and explain the literature about some specific important parameter.”
Meta-analysis compares how alternative study characteristics reflect on statistical findings; in other words, it aims to explain the source of variation among empirical results (Melo et al. 2009). As in this study, it is common in meta-analytic research to take the units of observation as estimates of a given coefficient and test the null hypothesis that this elasticity is zero (Rose, Stanley 2005). A general approach to render coefficients from different models and studies comparable is to represent the collected effect sizes in the form of elasticities (if they are provided as such), or to convert these effect sizes to elasticities if the primary study presents the necessary descriptive statistics to do so. A descriptive synthesis, followed by meta-regression analysis (elaborated below) would be helpful to identify the specific methodological differences leading to different results in terms of both direction and magnitude. Therefore, the researcher can gain new insight on how, for example, the inclusion of a certain variable or adoption of a different estimation strategy affects the results available in the literature. Changes in findings can also be observed with respect to samples used in the primary studies or the times in focus.
Results from meta-analytic research can potentially shed light on certain policy issues that require a research synthesis. Florax et al. (2002) draw attention to the area of applied, policy-related macroeconomics being quite open to the application of meta-analysis. Examples of recent applications of meta-analysis in economic policy include: Genc et al. (2012) on immigration and international trade; Cipollina, Pietrovito (2011) on trade and EU preferential agreements; Ozgen et al. (2010) on migration and income growth; Egger, Lassmann (2012) on common language and bilateral trade; Ridhwan et al. (2010) on monetary policy; De Groot et al. (2009) on externalities and urban growth; Doucouliagos, Laroche (2009) on unions and firm profits; Nijkamp, Poot (2004) on fiscal policies and growth; and Disdier, Head (2008) on the effect of distance on bilateral trade. Meta-analysis can be used to address the impact of differences between studies in terms of design of the empirical analysis; for example, with respect to the choice of explanatory variables (Nijkamp et al. 2011). Fundamentally, meta-analysis allows the researcher to combine results from several studies in order to reach a general conclusion (Holmgren 2007). In this regard, Cipollina, Salvatici (2010, 65) state “the main focus of MA [meta-analysis] is to test the null hypothesis that different point estimates, when treated as individual observations (...), are equal to zero when the findings from this entire area of research are combined.” In economics, however, the emphasis is placed on identification by means of meta-regression analysis (MRA) of a given quantitative impact, and on study characteristics that are statistically significant in explaining the variation in study outcomes (Poot 2014). Meta-regression analysis can be employed to discover how much the results obtained in primary studies are influenced by methodological aspects of the research together with the geographical and temporal attributes of the data used. Since the impacts of infrastructure on trade estimated in various studies differ widely in magnitude and significance, MRA can yield important results with respect to the choice of empirical and theoretical attributes of the primary study. We use the guidelines for MRA as published in Stanley et al. (2013). The methodology in this study can be broken into several components. We first descriptively report the observed variation in infrastructure elasticities of trade in Section 6. The results are reported based on several categorizations of study characteristics. Next, we employ a set of meta-regression models in Section 7 for a better understanding of the joint effect of the various study characteristics, while also taking possible publication bias explicitly into account. First, we briefly comment on study selection in the next section.
5 Data
The presence of at least one infrastructure-related factor among the explanatory variables in a primary study, and a dependent variable that represents export or import volumes or sales has been the main prerequisite in our data collection. Articles have been collected using the academic search engines JSTOR, EconLit, Google Scholar, SpringerLink, and Web of Science by using keywords such as “Infrastructure,” “Public Capital,” “Trade,” “Export,” “Import,” “Trade Facilitation,” and “Trade Costs” in various combinations. We are confident that our selected articles are the vast majority of comparable empirical studies on this topic. Studies that have not been published in English are the only obvious exception.
Numerous authors construct indexes representing the stock or level of infrastructure in the countries or regions that are used for primary analyses. An index can be based on a broad definition of infrastructure or on sub-categories, such as transportation or communication infrastructure. Depending on specific study attributes such as geographical coverage or spatial scale, infrastructure indexes are usually built by combining regional/national infrastructural data scaled by surface or population. Such indexes may include: road, railroad, or highway density/length, paved roads as a percentage of total road stock, number of fax machines, number of fixed and/or mobile phone line connections, number of computers, number of internet users, aircraft traffic and passengers, number of paved airports, maritime (port) traffic statistics, fleet share in the world, and electricity consumption. Some studies calculate these indexes either in a combined way for the trade partners, or separately for each partner, and sometimes also for the transit regions. For example, Bandyopadhyay (1999) uses road and railway, and phone network density separately as proxies for the technological level and the efficiency of the distribution sector. Using a sample of OECD economies, the author finds strong evidence that the distribution sector of an economy has important implications for its international trade performance.
An alternative to the index approach is the measurement of infrastructure in one or more specific ways in the statistical analysis. Focusing explicitly on railroads, phone connections, or port traffic can be examples of this approach. For example, Shepherd, Wilson (2006) focus specifically on roads and construct minimum and average road quality indexes for the trading partners. Similarly, Nordas, Piermartini (2004) also construct – in addition to considering an overall index – indexes for specific types of infrastructure and employ dummy variables in their estimation to represent infrastructure quality. These authors find a significant and positive impact of infrastructural quality on bilateral trade with port efficiency being the most influential variable in the model.
In our study, the effect size is defined as the infrastructure elasticity of trade. After selecting the studies that directly report the impact of exporter and/or importer infrastructure in comparable elasticities, and those that provided sufficient information for elasticities to be calculated, our data set consists of 542 effect sizes from 36 primary studies ranging from 1999 to 2012. Tables 1 and 2 describe the studies used in our analysis and report several descriptive statistics. The geographical coverage, estimation techniques, dependent variable choice (exports or imports), and the way in which infrastructure was measured are reported in Table 1. Table 2 summarizes the reported elasticities in each of the 36 studies, categorized by whether the dependent variable was exports or imports; whether the location of the infrastructure was at the point of production (exporter infrastructure); consumption (importer infrastructure); or measured as combined/transit infrastructure. Export equations yielded 307 elasticities within a considerable range of about -2 to +15 and an average value of 0.76. Import equations yielded 235 elasticities within the range of -2 and +8, with an average value of 0.38. Hence, regressions using export data clearly yielded larger elasticities.
Among our sample of 36 studies, 15 appear in peer-reviewed journals, while 21 studies are published as conference, discussion, or working papers, policy documents, or book chapters. Twelve studies were published by international organizations such as the World Bank, OECD, and WTO or had at least one author affiliated with these organizations.2 First, studies that only use a combined or transit infrastructure measure for both trade partners or estimate the impact of transit infrastructure that lies between partners were dropped. Second, one effect size, for which the standard error was reported as zero (which causes problems with the meta-regression), was dropped. Third, extreme outlier observations for exporter and importer infrastructure elasticities were dropped. Following this, twenty-seven studies and 379 effect sizes remain for all further analyses in this paper.3 Figure 1 shows the quantile plots of the effect sizes in our final data set for exporter infrastructure and importer infrastructure respectively. The ranges for the restricted data set are similar, but a comparison of the medians and the interquartile ranges suggest a tendency for exporter infrastructure elasticities to be somewhat larger.
| Table 2. Descriptive Statistics by Primary Study |
|
|
|
|
|||||
|
|
| Export Equation | Import Equation
| ||||||
|
Author(s) | Location of Infrastructure | Obs. | Mean | Min. | Max. | Obs. | Mean | Min. | Max.
|
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 8 | 0.35 | 0.14 | 0.52 | |||||
|
|
Importer Infrastructure | 8 | 0.01 | -0.23 | 0.29 | ||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Combined/Transit Inf. | 8 | 5.40 | 0.18 | 15.13 | |||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 4 | 0.56 | 0.46 | 0.64 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 3 | 1.10 | 1.10 | 1.11
| |||||
|
|
Combined/Transit Inf. | 4 | 0.64 | 0.58 | 0.77
| ||||
|
|
Importer Infrastructure | 4 | 1.38 | 1.32 | 1.45
| ||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 13 | 0.05 | -0.02 | 0.12 | |||||
|
|
Importer Infrastructure | 13 | -0.05 | -0.08 | 0.01 | ||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Combined/Transit Inf. | 4 | 0.33 | 0.21 | 0.38 | |||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 5 | 0.22 | 0.2 | 0.24
| |||||
|
|
Importer Infrastructure |
|
|
| 5 | 0.11 | 0.09 | 0.13
| |
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 3 | 0.70 | 0.67 | 0.73
| |||||
|
|
Importer Infrastructure | 3 | 0.45 | 0.35 | 0.55
| ||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 40 | 0.27 | -0.19 | 1.29
| |||||
|
|
Importer Infrastructure | 40 | 0.27 | -0.6 | 2.14
| ||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 11 | 0.91 | 0.54 | 1.06 | |||||
|
|
Importer Infrastructure | 11 | 0.28 | -0.28 | 0.47 | ||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 4 | 0.40 | 0.12 | 1.18
| |||||
|
|
Importer Infrastructure | 4 | 0.10 | 0.06 | 0.19
| ||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Combined/Transit Inf. | 12 | 1.72 | 1.17 | 2.77
| |||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 5 | 0.53 | -0.29 | 1.38 | |||||
|
|
Importer Infrastructure | 5 | 0.38 | -0.47 | 1.27 |
|
|
|
|
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 5 | 0.10 | 0.01 | 0.41
| |||||
|
|
Importer Infrastructure | 5 | 0.07 | 0.02 | 0.20
| ||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 2 | 0.08 | 0.03 | 0.13 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 10 | 0.37 | -0.66 | 1.47 | |||||
|
|
Importer Infrastructure | 10 | 0.3 | -1.4 | 2.15 | ||||
|
|
|||||||||
|
|
|||||||||
|
Combined/Transit Inf. | 32 | 0.46 | -2.09 | 1.5 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Exporter Infrastructure | 14 | 0.13 | -0.39 | 0.40
| |||||
|
|
Importer Infrastructure | 14 | -0.12 | -0.49 | 0.30
| ||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure |
|
|
|
| 38 | 0.16 | -0.01 | 1.17
| |
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 10 | 0.24 | 0.20 | 0.51
| |||||
|
|
Importer Infrastructure | 10 | 0.27 | 0.23 | 0.29
| ||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 11 | 1.05 | 0.68 | 1.76 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 1 | -0.07 | -0.07 | -0.07
| |||||
|
|
Importer Infrastructure | 1 | 0.02 | 0.02 | 0.02
| ||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 24 | 0.24 | -1.19 | 1.61 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Combined/Transit Inf. | 18 | 0.27 | -0.02 | 2.85 | |||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 4 | 1.36 | 1.22 | 1.69 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 1 | 0.05 | 0.05 | 0.05
| |||||
|
|
Importer Infrastructure | 1 | 0.05 | 0.05 | 0.05 | ||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 12 | 2.11 | 1.08 | 4.54 | |||||
|
|
Importer Infrastructure | 12 | 3.74 | -0.69 | 8.62 |
|
|
|
|
|
|
|||||||||
|
|
|||||||||
|
Importer Infrastructure | 9 | 0.91 | 0.66 | 1.68 | |||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 4 | -0.02 | -0.60 | 0.34 | |||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 6 | 1.90 | 1.58 | 2.07 | |||||
|
|
|||||||||
|
|
|||||||||
|
Combined/Transit Inf. | 9 | 1.69 | -2.36 | 8.10
| |||||
|
|
|||||||||
|
|
|||||||||
|
Importer Infrastructure | 8 | 0.23 | -0.17 | 0.58 | |||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 6 | 0.21 | 0.13 | 0.32 | |||||
|
|
|||||||||
|
|
|||||||||
|
Combined/Transit Inf. | 20 | 0.06 | -0.11 | 0.16 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 14 | -0.07 | -1.68 | 0.87 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
|
Exporter Infrastructure | 14 | 1.68 | 0.47 | 2.39 | |||||
|
|
|||||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|||||||||
|
Overall |
Any Infrastructure Location | 307 | 0.76 | -2.09 | 15.13 | 235 | 0.38 | -2.36 | 8.1
|
|
|
|||||||||
|
|
|||||||||
|
|
|||||||||
6 Descriptive Analysis
In order to conduct descriptive and regression analyses, the methodological attributes together with various other characteristics of the primary studies are coded numerically as binary variables. Definitions of the variables representing the study characteristics are provided in Table 3.
Overall, approximately 82 percent of the estimates in the final data set find a positive and significant infrastructure impact on trade. The descriptive statistics for all effect sizes are grouped by direction of trade, methodology, infrastructure category, development level of the relevant economies, and publication status. The results are presented in Tables 4, 5, 6, 7, 8. For ease of comparison, the combined descriptive statistics for all groups are repeated in the bottom line of each table.4
Table 4 reinforces the earlier finding from Table 2 that studies where the dependent variable was exports, on average, yielded higher effect sizes than studies that use imports as the dependent variable. Thus, according to these raw averages, the mean effect size on exports is larger than on imports regardless of the location of infrastructure. However, irrespective of the trade data used (imports or exports), exporter infrastructure has a bigger impact than importer infrastructure, with elasticities on average 0.34 and 0.16 respectively. This implies a net gain in the balance of merchandise trade from expanding infrastructure in a particular country, an important finding which we will quantify further after controlling for study heterogeneity and publication bias.5
Nevertheless, the greater impact of exporter infrastructure is not the case across all types of estimation methods (see Table 5). Heckman, Tobit, and Probit estimations (that control for zero trade flows) yield larger importer infrastructure elasticities than exporter elasticities (0.49 and 0.33 respectively). When considering the type of infrastructure (see Table 6), a composite measure has a bigger impact than the more specific infrastructure types of land transport, maritime or air transport, and communication infrastructure. By leaving aside the composite measure category, however, land transportation infrastructure appears on average, to affect trade in both directions more than the other types of infrastructure. Exporter infrastructure has again, on average, a higher effect size on trade than importer infrastructure for all categories except communication infrastructure. This is an interesting finding, as communication infrastructure has a greater impact on transaction costs than on transportation costs, because it facilitates the flow of information, which can enhance trade. It appears that communication infrastructure has a greater impact on the consumption side of the market than on the production side. Meta-regression analysis will show that this effect is statistically significant in the model that corrects for publication bias.
In order to account for differences regarding the level of development of the economies included in the primary studies, the grouping of results is based on three types of data sets. A “Developed Economies” category is used when the author uses terms such as “Developed,” “Rich,” “North,” “OECD,” and “EU” to describe the part of the sample in which the infrastructure is located in the primary study. “Developing Economies” is used if the classification is described as “Developing,” “South,” or “Poor.”6 In order to examine the estimates obtained from samples that included both developed and developing countries, a “Mixed Samples” category was defined. Results are presented in Table 7. The average elasticity in mixed samples is in between those for developed countries and developing countries for exporter infrastructure. In all categories, the elasticity of exporter infrastructure is larger than that of importer infrastructure. Less developed economies seem to enjoy a higher return on infrastructure (especially if it is exporter infrastructure) compared to developed economies. This difference may be attributed to diminishing returns to investment in infrastructure capital, as is consistent with the neoclassical theory of long-run development.
In Table 8, we consider a measure of publication quality of the research by adopting the Australian Business Deans Council Journal Quality List (Australian Business Deans Council (ABDC) 2010). “Highly Ranked Journals” refers to papers published in journals classified as A*, A, or B. “Other journals and unpublished” refers to outlets with classification C or D (category D includes book chapters, non-refereed working papers and conference proceedings). Exporter infrastructure has again higher average effect sizes than importer infrastructure for all categories. Moreover, studies in highly ranked journals find on average higher effect sizes for both exporter and importer infrastructure compared to other studies. In meta-analysis, this is commonly attributed to publication bias on which we elaborate further in Section 7.
The raw mean values that are presented in Tables 4, 5, 6, 7, and 8 must be treated with caution, as they pool the information obtained from primary studies without considering the standard errors of the estimates. If there is no unobserved heterogeneity in the meta-data, and study characteristics do not play a role in explaining the variation in the estimated effect sizes, the fixed effect (FE) combined estimate is a more efficient average than the ordinary mean (Genc et al. 2012). The FE estimate is a weighted average of effect sizes where the inverse of the estimated variance of each effects size is taken as the weight (Genc et al. 2012). If there is heterogeneity among studies, but not in a systematic way that can be measured by study characteristics, the Random Effect (RE) weighted average accounts for such variability. We calculated the FE and RE estimates as described by Poot (2014) and others.
| Exporter Infrastructure | Importer Infrastructure
| |||||||
| Obs | Mean | Min | Max | Obs | Mean | Min | Max | |
| Exports | 129 | 0.50 | -1.19 | 1.88 | 70 | 0.22 | -1.40 | 1.78 |
| Imports | 108 | 0.15 | -0.39 | 0.61 | 72 | 0.09 | -0.44 | 0.59 |
| Overall | 237 | 0.34 | -1.19 | 1.88 | 142 | 0.16 | -1.40 | 1.78 |
| Exporter Infrastructure | Importer Infrastructure
| ||||||||
| Obs | Mean | Min | Max | Obs | Mean | Min | Max | ||
| Heckman Sample Selection, Tobit, or Probit | 82 | 0.33 | -1.19 | 1.76 | 15 | 0.49 | -0.69 | 1.68 | |
| IV or Other Control for Endogeneity | 24 | 0.44 | 0.01 | 1.88 | 19 | 0.15 | -0.23 | 0.29 | |
| Other Estimation Method | 133 | 0.32 | -0.66 | 1.69 | 108 | 0.11 | -1.40 | 1.78 | |
| Overall | 237 | a | 0.34 | -1.19 | 1.88 | 142 | 0.16 | -1.40 | 1.78 |
| Exporter Infrastructure | Importer Infrastructure
| |||||||
| Obs | Mean | Min | Max | Obs | Mean | Min | Max | |
| Land Transport Infrastructure | 43 | 0.36 | -0.66 | 1.61 | 22 | 0.15 | -1.4 | 1.78 |
| Maritime or Air Transport Infrastructure | 13 | 0.16 | -0.07 | 0.61 | 11 | 0.14 | -0.1 | 0.59 |
| Communication Infrastructure | 56 | 0.08 | -1.19 | 0.71 | 20 | 0.12 | -0.21 | 0.58 |
| Composite Measure (Index) | 125 | 0.47 | -0.9 | 1.88 | 89 | 0.17 | -0.69 | 1.68 |
| Overall | 237 | 0.34 | -1.19 | 1.88 | 142 | 0.16 | -1.40 | 1.78 |
| Exporter Infrastructure | Importer Infrastructure
| |||||||
| Obs | Mean | Min | Max | Obs | Mean | Min | Max | |
| Developed Economy | 9 | 0.32 | 0.12 | 0.52 | 11 | 0.05 | -0.23 | 0.34 |
| Developing Economy | 72 | 0.49 | -1.19 | 1.88 | 11 | 0.07 | -1.40 | 1.78 |
| Both Types of Economies (Mixed Sample) | 156 | 0.27 | -0.90 | 1.44 | 120 | 0.18 | -0.69 | 1.68 |
| Overall | 237 | 0.34 | -1.19 | 1.88 | 142 | 0.16 | -1.40 | 1.78 |
| Exporter Infrastructure | Importer Infrastructure
| |||||||
| Obs | Mean | Min | Max | Obs | Mean | Min | Max | |
| Highly Ranked Journals | 67 | 0.40 | -0.90 | 1.88 | 44 | 0.20 | -0.23 | 1.68 |
| Other Journals and Unpublished | 170 | 0.31 | -1.19 | 1.69 | 98 | 0.14 | -1.40 | 1.78 |
| Overall | 237 | 0.34 | -1.19 | 1.88 | 142 | 0.16 | -1.40 | 1.78 |
Because effect sizes come from studies with different geographical coverage, methodology, and model specifications, it is questionable whether there would be an underlying universal effect size. This can be formally confirmed by means of a homogeneity test using a commonly used “Q-statistic” (Engels et al. 2000). The Q-statistic (computation as in Peters et al. 2010) tests if the primary studies share a common effect size and whether an FE estimate is relevant to the analysis (Poot 2014). After combining K effect sizes, if the resulting Q-statistic from this homogeneity test is greater than the upper-tail critical value of the chi-square distribution with K - 1 degrees of freedom, then the variance in effect sizes obtained from the primary studies is significantly greater than what can be observed due to random variation around a common effect size (Shadish, Haddock 1994). If the existence of a shared true effect is rejected, the FE approach is not suitable, and only the RE estimates should be considered (Poot 2014).
The Q-statistics for exporter infrastructure and importer infrastructure respectively are about 33174.7 and about 4596.1 which both exceed the critical value of 493.6. Based on this outcome of the Q-test we conclude that effect sizes are from a highly heterogeneous pool of studies, and FE weighted average effect sizes are not meaningful.7 The RE average effect sizes for exporter and importer infrastructure are 0.167 and 0.145 respectively. Consequently, the result that exporter infrastructure is more influential on trade than importer infrastructure is supported. The RE estimates suggest that an enhancement in exporter infrastructure of 1 percent would increase annual merchandise trade by about 0.17 percent while importer infrastructure increases trade by about 0.15 percent. In the next section, we re-assess this conclusion by controlling for study characteristics and publication bias.
7 Meta-regression models
The statistical consequence of the potential unwillingness by researchers or reviewers to publish statistically insignificant results is defined as “publication bias” or “file drawer bias.” The actions leading to publication bias can be the efforts of the researchers using small samples towards obtaining large-magnitude estimates (that are statistically significant), while researchers using large samples do not need to exhibit such efforts and report smaller estimates that are still statistically significant. This selection process results in positive correlation between the reported effect size and its standard error (Stanley 2005, Stanley et al. 2008). As an initial exploration of the possibility of such bias, we apply Egger’s regression test8 (Egger et al. 1997) and the Fixed Effects Extended Egger Test9 (Peters et al. 2010). The results of both tests for exporter and importer infrastructure are reported in Table 9. Both variants of the test yield significant coefficients on the bias term when testing for publication bias in the impact estimates of exporter infrastructure. The evidence for bias in the estimation of the impact of importer infrastructure is less conclusive, having been confirmed with the Egger test but not with the extended Egger test. The greater bias in estimating exporter infrastructure impact will also be demonstrated with the Hedges et al. (1992) model of publication bias.
| Egger Test | Extended Egger Test
| |||
| Exporter Inf. | Importer Inf. | Exporter Inf. | Importer Inf.
| |
| Bias | 7.009*** | 2.308*** | 4.318*** | -0.464
|
| (0.632) | (0.566) | (0.736) | (0.442)
| |
| Observations | 237 | 142 | 237 | 142
|
| R-squared | 0.344 | 0.106 | 0.705 | 0.852
|
| Standard errors in parentheses
| ||||
| *** p < 0.01, ** p < 0.05, * p < 0.1
| ||||
The Hedges model is an extension of the RE model in which it is assumed that the likelihood of a result being publicly reported is greatest when the associated p-value of the coefficient of the variable of interest is smaller than 0.01. While this likelihood remains unknown, two relative probabilities, denoted here by ω2 and ω3, are associated with the cases: 0.01 < p < 0.05 and p > 0.05 respectively. We use the method proposed by Ashenfelter et al. (1999) to formulate a likelihood function to estimate ω2 and ω3. These parameters should be equal to 1 if publication bias is not present. Table 10 presents the estimates associated with the Hedges publication bias procedure. In part (a) of Table 10 we consider the case in which there is no observed heterogeneity assumed, i.e. there are no study characteristics that act as covariates. In part (b) of Table 10, covariates are included. The model is estimated under the restriction that the probabilities of publication are all the same on the RHS of the table, while the LHS of the table estimates the relative probabilities with maximum likelihood.
On the LHS of Table 10 (a), we see that less significant estimates are less likely to be reported. The corresponding weights for 0.01 < p < 0.05 and p > 0.05 are 0.739 and 0.137 for exporter’s infrastructure, and 0.280 and 0.120 for imports. The RHS shows the results of the restricted model which assumes ω2 = ω3 = 1 (no publication bias). The chi-square critical value at 1 percent level with two degrees of freedom is 9.21. Two times the difference between the log-likelihoods of assuming and not assuming publication bias is 63.28 for exporter’s infrastructure without study characteristics and 51.2, with study characteristics – in both cases greatly exceeding the critical value and providing evidence for publication bias at the 1 percent level. Similarly, evidence for the existence of publication bias is also observed for importer infrastructure, with test statistics of 53.62 and 151.8 for without and with covariates respectively.
We can also see that residual heterogeneity decreases considerably upon the introduction of study characteristics for both exporter and importer infrastructure (from 0.341 to 0.255 and from 0.231 to 0.0302 respectively). Accounting for publication bias and study heterogeneity (Table 10b) lowers the RE estimate of the exporter infrastructure elasticity from 0.300 to 0.254 but leaves the RE estimate of the importer infrastructure elasticity relatively unaffected (0.256 and 0.259 respectively). This is consistent with the result of the extended Egger test reported above.
Taking into account the heterogeneity that is apparent in our data set, as demonstrated formally by the Q-statistic, we now conduct MRA in order to account for the impact of study characteristics on study effect sizes.
The simplest MRA assumes that there are S independent studies (s = 1,2,...,S) which each postulate the classic regression model y(s) = X(s)β(s) + ϵ(s), with the elements of ϵ(s) identically and independently distributed with mean 0 and variance σ2(s). Study s has N(s) observations and the vector β(s) has dimension K(s) × 1. The first element of this vector is the parameter of interest and has exactly the same interpretation across all studies (in our case it is either the exporter infrastructure elasticity of trade or the importer infrastructure elasticity of trade).
Under these assumptions, a primary study would estimate β(s) by the OLS estimator
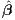 (s) = [X(s)′X(s)]-1[X(s)′y(s)], which is best asymptotically normal distributed with mean
β(s) and covariance matrix σ2(s)[X(s)′X(s)]-1. The S estimates of the parameter of interest
are the effect sizes. We observe the effect sizes
(s) = [X(s)′X(s)]-1[X(s)′y(s)], which is best asymptotically normal distributed with mean
β(s) and covariance matrix σ2(s)[X(s)′X(s)]-1. The S estimates of the parameter of interest
are the effect sizes. We observe the effect sizes 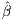 1(1),
1(1),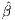 1(2),…,
1(2),…,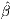 1(s). Given the data generating
process for the primary studies,
1(s). Given the data generating
process for the primary studies,
![ˆ ′ -1 ′
β1(s) = β1(s)+ [[X (s) X (s)] X (s) ϵ(s)]1](25-CE-4html21x.png) | (7) |
which are consistent and efficient estimates of the unknown parameters β1(1),…,β1(S). These
effect sizes have estimated variances v(1),…,v(S). In study s, v(s) is the top left element of the
matrix 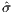 2(s)[X(s)′X(s)]-1 with
2(s)[X(s)′X(s)]-1 with 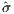 2(s) = [e(s)′e(s)]′∕N(s), and e(s) = y(s) -X(s)
2(s) = [e(s)′e(s)]′∕N(s), and e(s) = y(s) -X(s)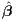 (s) is the
vector of least square residuals.
(s) is the
vector of least square residuals.
| (a) Study characteristics not considered
| |||||
| Exporter inf. | Exporter inf.
| ||||
| assuming publication bias | not assuming publication bias
| ||||
| SE | SE
| ||||
| ω2 | 0.739*** | (0.193) | ω2 | ||
| ω3 | 0.137*** | (0.0395) | ω3 | ||
| RE | 0.225*** | (0.0231) | RE | 0.292*** | (0.0262) |
| τ | 0.341*** | (0.0177) | τ | 0.382*** | (0.0209) |
| Log-likelihood | 109.7 | Log-likelihood | 78.06 | ||
| n | 237 | n | 237 | ||
| Importer inf. | Importer inf.
| ||||
| assuming publication bias | not assuming publication bias
| ||||
| SE | SE
| ||||
| ω2 | 0.280*** | (0.105) | ω2 | ||
| ω3 | 0.120*** | (0.0368) | ω3 | ||
| RE | 0.101*** | (0.0187) | RE | 0.158*** | (0.0272) |
| τ | 0.231*** | (0.0165) | τ | 0.300*** | (0.0228) |
| Log-likelihood | 97.84 | Log-likelihood | 71.03 | ||
| n | 142 | n | 142 | ||
| (b) Study characteristics considered
| |||||
| Exporter inf. | Exporter inf.
| ||||
| assuming publication bias | not assuming publication bias
| ||||
| SE | SE
| ||||
| ω2 | 0.747*** | (0.196) | ω2 | ||
| ω3 | 0.156*** | (0.0464) | ω3 | ||
| RE | 0.254*** | (0.0199) | RE | 0.300*** | (0.021) |
| τ | 0.255*** | (0.0145) | τ | 0.273*** | (0.0163) |
| Log-likelihood | 168.3 | Log-likelihood | 142.7 | ||
| n | 237 | n | 237 | ||
| Importer inf. | Importer inf.
| ||||
| assuming publication bias | not assuming publication bias
| ||||
| SE | SE
| ||||
| ω2 | 0.0716*** | (0.0266) | ω2 | ||
| ω3 | 0.0142*** | (0.00409) | ω3 | ||
| RE | 0.259*** | (0.0191) | RE | 0.256*** | (0.0499) |
| τ | 0.0302*** | (0.0059) | τ | 0.136*** | (0.016) |
| Log-likelihood | 210 | Log-likelihood | 134.1 | ||
| n | 142 | n | 142 | ||
MRA assumes that there are P known moderator (or predictor) variables M1,…,MP that are related to the unknown parameters of interest β1(1),…,β1(S) via a linear model as follows:
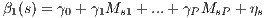 | (8) |
in which Msj is the value of the jth moderator variable associated with effect size s and the ηs are independently and identically distributed random variables with mean 0 and variance τ2 (the between-studies variance). Thus, equation (8) allows for both observable heterogeneity (in terms of observable moderator variables) and unobservable heterogeneity (represented by ηs). By combining (7) and (8), the MRA model becomes
![( )
|{ ′ ′ |}
ˆβ1(s) = γ0 + γ1Ms1 + ...γPMsP + | η◟s +-[[X-(s)-X-(◝s)◜]-1X-(s)-ϵ(s)]1◞|
( Error term of MRA )](25-CE-4html26x.png) | (9) |
with the term in the curly brackets being the error term of the MRA. The objective of
MRA is to find estimates of γ0,γ1,...γP that provide information on how observed
estimates of the coefficients of the focus variable are linked to observed study
characteristics. Typically, the meta-analyst observes for each s = 1,2,...,S : 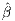 1(s);
its estimated variance
1(s);
its estimated variance 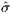 2(s)[[X(s)′X(s)]-1]11; the number of primary study
observations N(s), and information about the variables that make up X(s), possibly
including means and variances, but not the actual data or the covariances between
regressors.10
The P known moderator variables M1,M2,...MP are assumed to capture information about
the covariates and the estimation method in case the estimations were obtained by techniques
other than OLS. The error term in regression model (9) is clearly heteroskedastic and
generates a between-study variance due to ηs and a within-study variance due to
[[X(s)′X(s)]-1X(s)′ϵ(s)]1.
2(s)[[X(s)′X(s)]-1]11; the number of primary study
observations N(s), and information about the variables that make up X(s), possibly
including means and variances, but not the actual data or the covariances between
regressors.10
The P known moderator variables M1,M2,...MP are assumed to capture information about
the covariates and the estimation method in case the estimations were obtained by techniques
other than OLS. The error term in regression model (9) is clearly heteroskedastic and
generates a between-study variance due to ηs and a within-study variance due to
[[X(s)′X(s)]-1X(s)′ϵ(s)]1.
We apply two different estimation methods for equation (9):11
- a.
- Restricted Maximum Likelihood (REML): In REML the between-study variance is estimated by maximizing the residual (or restricted) log likelihood function and a WLS regression weighted by the sum of the between-study and within-study variances is conducted to obtain the estimated coefficients (Harbord, Higgins 2008). The standard error does not enter as an individual variable into this specification.
- b.
- The publication bias corrected maximum likelihood procedure proposed by Hedges et al. (1992) and outlined above.
The results of the estimation of equation (9) with the REML and Hedges estimators are shown in Table 11. All explanatory variables are transformed in deviations from their original means. We analyze the results separately for each category of variables.
7.1 Methodology
Results from the Hedges model suggest that studies taking into account zero trade flows using Heckman sample selection, Tobit, or Probit models, on average, estimate a lower effect size for exporter infrastructure, and a higher effect size for importer infrastructure. For robustness checks, OLS and WLS estimates are reported in the appendix. On the matter of sample selections, the results are not consistent across MRAs. In what follows, we pay most attention to the results of the Hedges model because this is the only model that accounts for publication bias but also emphasize those results that are found in the other MRAs as well.
According to both the REML and Hedges results, studies that use instrumental variable methods to deal with potential endogeneity observe a larger impact of exporter infrastructure on trade. Consequently, econometric methodology is an important study characteristic that affects the results. Not accounting for endogeneity of exporter infrastructure leads to an underestimation of its impact on trade. This is not the case for importer (consumer) infrastructure.
Whether a primary study uses a gravity model or not does not seem to have an influence. For importer infrastructure, this variable drops out. This is because, naturally, there are no effect sizes in our sample resulting from a regression where the importing partner’s infrastructure is included and the model is not in gravity form. Implicitly, the inclusion of the Gravity model dummy also asks if the distance between trade partners has been considered in the primary estimations, as distance is an essential component of a gravity specification.
7.2 The Point at Which the Trade is Measured
In both the REML and Hedges estimations, the coefficient of the dummy Dependent variable is exports is significant and positive for exporter infrastructure, suggesting that own infrastructure has a greater impact when trade is measured by export data rather than by import data. This is also found in the OLS and WLS MRAs in the appendix. As discussed in Section 3, in a primary study where all bilateral trading partners would be included and all trade is measured with transaction costs included (cif), the two effect sizes must be equal. However, data on any trade flow may differ depending on measurement at the point of shipment or at the point of importation. Moreover, as noted previously, trade matrices may not be square, such as in an analysis of developing country exports to developed countries. For the same variable, the Hedges model yields a significant and negative coefficient for importer infrastructure, suggesting that the impact of the infrastructure located in the importing economy is lower when measured with respect to the exports of its partner than with respect to its own imports.
Using the Hedges model, we can predict the overall impacts of exporter (producer) infrastructure and importer (consumer) infrastructure by combining these coefficients with the constant terms, which measure the overall average effects. The results can be directly compared with the “raw” averages reported in Table 4. We get:
- The own infrastructure of country i has an average effect size of 0.254 + 0.345 = 0.599 on the exports of i;
- The own infrastructure of country i has an average effect size of 0.259 on the imports of i;
- The infrastructure in the partner country j of the exporting country i has an average effect size of 0.254 on the imports of i;
- The infrastructure in the partner country j of the exporting country i has an average effect size of 0.259 - 0.126 = 0.133 on the exports of i.
We see that after controlling for heterogeneity and publication bias, the exporter infrastructure effect continues to be larger when measured with export data than with import data, (0.599 versus 0.254 above, compared with 0.50 and 0.15 respectively in Table 4), while for importer infrastructure the opposite is the case (0.133 versus 0.259 above, and 0.22 versus 0.09 respectively in Table 4). The most important result from this analysis is that from the perspective of any given country, the impact of own infrastructure on net trade (assuming roughly balanced gross trade) is 0.599 - 0.259 = 0.340. Alternatively, if we take the average of the exporter infrastructure elasticities 0.599 and 0.254, and subtract the average of the importer infrastructure elasticities (0.133 and 0.259), we get a net trade effect of 0.23. Averaging the calculations from both perspectives, an increase in own infrastructure by 1 percent increases net trade by about 0.3 percent. We address the macroeconomic implication of this finding in Table 8.
7.3 Infrastructure category
As discussed earlier, infrastructure is defined as a collection, or portfolio, of various components. Consequently, in our estimations, four common measurements of infrastructure are accounted for (land, maritime or air, communication, and a composite index). Aside from the REML model for importer infrastructure, all our estimations suggest that land transport infrastructure is estimated to have a larger effect size on trade than the other infrastructure categories, on average. The Hedges model suggests that maritime and air transportation infrastructure and communication infrastructure on the importer side have higher average effect sizes compared to elasticities obtained from composite infrastructure indexes.
7.4 Development level of the economy in which the infrastructure is located
Both the REML and Hedges results suggest that exporter infrastructure matters more for trade if the exporting economy is developing rather than developed (also shown by the OLS model in the appendix). This result was noted previously and is commonly found in the literature. Moreover, importer infrastructure is less influential in trade when the importing economy is developed (also shown with the WLS model in the appendix).
7.5 Sample structure
The Hedges, REML, OLS, and WLS MRAs all suggest that a lower infrastructure elasticity of trade for importer infrastructure has been observed in estimates obtained from studies where the units of analysis were sub-regional or firm level. The same is found for exporter infrastructure, but only in the Hedges model. Sub-regional samples force the location where trade takes place and the location of infrastructure to be measured (spatially) closer to one another. Therefore, such samples do not capture spillovers to the rest of the economy. The negative result on the variable Sub-national or firm level suggests that the estimated macro effects are larger than the micro effects.
7.6 Model specification
The dummy variables are defined such that they are equal to unity when a particular covariate has been omitted from the primary regression. Consequently, the coefficients provide an explicit measure of omitted variable bias. The Hedges model results show some evidence that for estimations that do not control for other infrastructure types (for example, if only road infrastructure is considered), the impact of importer infrastructure on trade is likely to be overestimated. The REML and Hedges models suggest that similar positive omitted variable bias arises for the importer infrastructure elasticity of trade when exporter infrastructure is not jointly considered (this is also found in the OLS and WLS MRAs).
Both models also suggest that excluding income and tariff or trade agreement variables can bias the estimate on exporter infrastructure downwards, while – based on the Hedges results – an upward bias for importer infrastructure can result if tariffs or trade agreements are not controlled for. Both models suggest that omitting variables for education or human capital can cause a downward bias in the estimation of the importer infrastructure elasticity of trade (also found in the OLS and WLS MRAs). The same can be found in the estimation of both the exporter and importer infrastructure effect size based on the results of both models if governance-related variables such as rule of law and corruption are omitted. Not considering population can cause the effect size of importer elasticity to be overestimated according to the Hedges results. Omitting the exchange rate in the trade regression leads to upward bias in the estimate for exporter infrastructure (also confirmed by the OLS and WLS MRAs).
7.7 Nature of publication
The Hedges model provides some evidence that studies, which were published in highly ranked journals, have estimated a larger effect size of importer infrastructure compared to other studies. A similar result is visible for the advocacy variable: research published by institutes with potential advocacy motives for announcing a larger infrastructure effect have estimated, on average, a higher effect size for importer infrastructure. All advocacy coefficients are positive, but for exporter infrastructure, only the result of the WLS estimation reported in the appendix is statistically significant.
7.8 Model prediction
A final useful exercise is to consider the goodness of fit of an MRA with respect to the set of effect sizes reported in the original studies. For this purpose, we predicted the mean squared error (MSE) of the comparison between the observed effect sizes and those predicted by the REML model for each study (predictions by the Hedges model are more cumbersome). The MSE for each study is reported in Table 12a for exporter infrastructure and Table 12b for importer infrastructure. Among the studies that contributed to both MRAs, the REML soundly describes the studies of Raballand (2003), Grigoriou (2007), Bandyopadhyay (1999), Carrere (2006) and Brun et al. (2005). On the other hand, studies by Iwanow, Kirkpatrick (2009), Fujimura, Edmonds (2006) and Marquez-Ramos, Martinez-Zarzoso (2005) yield results that are not closely aligned with what the REML MRAs suggested.
| Author | MSE |
| Kurmanalieva, Parpiev (2008) | 0.002 |
| Brun et al. (2005) | 0.005 |
| Raballand (2003) | 0.023 |
| Bandyopadhyay (1999) | 0.043 |
| Persson (2007) | 0.053 |
| Carrere (2006) | 0.058 |
| Nordas, Piermartini (2004) | 0.063 |
| Elbadawi (1999) | 0.087 |
| Francois, Manchin (2007) | 0.111 |
| Grigoriou (2007) | 0.151 |
| Njinkeu et al. (2008) | 0.167 |
| Wilson et al. (2004) | 0.202 |
| Martinez-Zarzoso, Nowak-Lehmann (2003) | 0.211 |
| Fujimura, Edmonds (2006) | 0.389 |
| Ninkovic (2009) | 0.442 |
| De (2007) | 0.445 |
| UN Economic Commission for Africa (UNECA) (2013) | 0.518 |
| Vijil, Wagner (2012) | 0.925 |
| Portugal-Perez, Wilson (2012) | 1.014 |
| Marquez-Ramos, Martinez-Zarzoso (2005) | 1.047 |
| Iwanow, Kirkpatrick (2007) | 1.969 |
| Bouet et al. (2008) | 2.013 |
| Elbadawi et al. (2006) | 7.348 |
| Granato (2008) | 7.727 |
| Author | MSE |
| Raballand (2003) | 0.000 |
| Grigoriou (2007) | 0.006 |
| Bandyopadhyay (1999) | 0.012 |
| Carrere (2006) | 0.012 |
| Jansen, Nordås (2004) | 0.014 |
| Brun et al. (2005) | 0.016 |
| Martinez-Zarzoso, Nowak-Lehmann (2003) | 0.02 |
| Wilson et al. (2004) | 0.026 |
| Nordas, Piermartini (2004) | 0.067 |
| Kurmanalieva, Parpiev (2008) | 0.116 |
| Persson (2007) | 0.118 |
| De (2007) | 0.147 |
| Njinkeu et al. (2008) | 0.149 |
| Iwanow, Kirkpatrick (2009) | 0.461 |
| Fujimura, Edmonds (2006) | 0.541 |
| Marquez-Ramos, Martinez-Zarzoso (2005) | 0.541 |
| Lawless (2010) | 0.672 |
8 Concluding Remarks
In this study, we have applied meta-analytic techniques to estimate the impact of exporter and importer infrastructure on trade and to examine the factors that influence the estimated elasticities of this impact. The initial data set consisted of 542 estimates obtained from 36 primary studies. We observe evidence that publication (or file drawer) bias exists in this strand of literature and apply the Hedges publication bias procedure.
The key result of our research is that the own infrastructure elasticity of the exports of a country is about 0.6 and own infrastructure elasticity on the imports of a country is about 0.3. This finding suggests that exports would respond to an improvement in the overall trade-related infrastructure more than imports, and that an expansion of the interrelated and integrated components of total trade-related infrastructure may have an attractive return through its impact on the external trade balance.
This result can be further elaborated: Assume that in a given economy, infrastructure is valued at about 50 percent of GDP.12 The resource cost of a 1 percent increase in infrastructure would therefore be about 0.5 percent of GDP. As the Hedges MRA results suggest that such an increase in infrastructure will increase exports by about 0.6 percent and imports by about 0.3 percent, if exports and imports are of similar magnitude, net exports will then increase by about 0.3 percent of the value of exports. This impact on GDP clearly depends on the openness of the economy (as measured by the exports to GDP ratio) and the short-run and long-run general equilibrium consequences. In turn, these will depend on the assumptions made and the analytical framework adopted. Nevertheless, even under conservative assumptions, the additional infrastructure is likely to have an expansionary impact in the short-run (although the size of any multiplier remains debated, see e.g. Owyang et al. 2013), and in the long-run through increasing external trade. For reasonable discount rates and sufficiently open economies, it is easy to construct examples that yield attractive benefit-cost ratios for such infrastructure investment. Additionally, a common argument is that expansionary policy may yield further productivity improvements.
The question remains what causes this differential impact of infrastructure on exports vis-a-vis imports. Consider the export demand function as presented by Anderson, van Wincoop (2003):
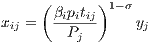 | (10) |
Equation (10) implies that a decline in t due to improved infrastructure raises the demand for country or region i’s exports. Given that an exporting firm is a price taker in the foreign market and bears the transportation costs to compete there, increases in the stock or quality of origin infrastructure raise the profitability of exports to all possible destinations. On the other hand, from the point of view of a foreign firm that supplies imports to country i, this infrastructure enhancement in the home economy lowers the cost of transportation to one destination only. Thus, an increase in infrastructure affects all exports of the local firm but it only affects a proportion of the exports of the foreign firm. Because imports may be more income elastic than price elastic, the effect of the decrease in the price of imports (which already included the foreign freight and insurance) relative to the domestic price will be small. Consequently, the change in infrastructure in country i impacts the behavior of the foreign firm that produces the imports less than that of the domestic firm that produces exports (assuming the infrastructure in other countries remained constant). Therefore, the marginal impact is at least initially larger on exports than on imports. It is important to underline that this conclusion is based on the ceteris paribus assumption. On average, infrastructural investment in a certain country may only be expected to improve if no trading partners improve their infrastructures in similar proportions. Trade is a zero-sum game and the trade balance of an economy will only improve given that no economies in the rest of the world improve their infrastructures in similar proportions.
Moreover, there may also be structural asymmetries and intangible aspects adding to this difference in the exporter and importer infrastructure elasticities of trade. Infrastructure may be tailored more towards exports and not be neutral to the direction of trade. Even if the quality and stock of infrastructure is identical, the way it is utilized may differ between the incoming and outgoing traffic of goods. Differences between the two functions of the same infrastructure can be due to choices such as the amount of personnel allocated or prices charged for infrastructure utilization. Political factors may be another possibility that causes this asymmetry. If exporters politically have more lobbying power than importers, new infrastructure approved by governments may be biased to benefit exporters more than importers. The literature would therefore benefit from further research on microeconomic mechanisms that yield the “stylized facts” that we have uncovered in this meta-analysis.
Finally, our research provides crucial synthesized evidence for developing economies or even low-income economies where infrastructure deprivation is a fact. For instance, the 2005 report of the Commission for Africa emphasizes the need of a functioning transport and communications system for Africa and states that the continent’s transport costs “local, national, and international - are around twice as high as those for a typical Asian country” and “to improve its capacity to trade Africa needs to make changes internally. It must improve its transport infrastructure to make goods cheaper to move” (Commission for Africa 2005, 14, 102). Our meta-analytic evidence adds useful evidence to back the argument that areas with poor infrastructure, such as parts of Africa, could greatly benefit from trade-enhancing infrastructure oriented policy measures.
References
Anderson JE, van Wincoop E (2003) Gravity with gravitas: A solution to the border puzzle. American Economic Review 93: 170–192
Anderson JE, van Wincoop E (2004) Trade costs. Journal of Economic Literature 42: 691–751
Ashenfelter O, Harmon C, Oosterbeek H (1999) A review of estimates of the schooling/earnings relationship, with tests for publication bias. Labour Economics 6: 453–470
Australian Business Deans Council (ABDC) (2010). Australian Business Deans Council Journal Quality List. Retrieved on September 24, 2012 from http://www.abdc.edu.au/
Bandyopadhyay U (1999) Trade and the distribution sector: Some evidence from OECD countries. The Canadian Journal of Economics / Revue canadienne d’Economique 32: 1299–1312
Becker BJ, Wu MJ (2007) The synthesis of regression slopes in meta-analysis. Statistical Science: 414–429
Bergstrand JH (1985) The gravity equation in international trade: Some microeconomic foundations and empirical evidence. The Review of Economics and Statistics 67: 474–481
Biehl D (1986) The contribution of infrastructure to regional development: final report / by Dieter Biehl, Infrastructure Study Group. Office for Official Publications of the European Communities; European Community Information Service, Luxembourg, Washington DC
Bikker JA (1987) An international trade flow model with substitution: an extension of the gravity model. Kyklos 40: 315–337
Bouet A, Mishra S, Roy D (2008) Does Africa trade less than it should, and if so, why?: the role of market access and domestic factors. International Food Policy Research Institute, Washington DC
Bougheas S, Demetriades PO, Morgenroth EL (1999) Infrastructure, transport costs and trade. Journal of International Economics 47: 169–189
Bruinsma F, Nijkamp P, Rietveld P (1989) Employment impacts of infrastructure investments: a case study for the Netherlands. Serie Research MeMoranda 0051, VU University Amsterdam, Faculty of Economics, Business Administration and Econometrics, Amsterdam
Brun JF, Carrère C, Guillaumont P, De Melo J (2005) Has distance died? Evidence from a panel gravity model. The World Bank Economic Review 19: 99–120
Buys P, Deichmann U, Wheeler D (2010) Road network upgrading and overland trade expansion in Sub-Saharan Africa. Journal of African Economies 19: 399–432
Carrere C (2006) Revisiting the effects of regional trade agreements on trade flows with proper specification of the gravity model. European Economic Review 50: 223–247
Casas FR (1983) International trade with produced transport services. Oxford Economic Papers 35: 89–109
Cipollina M, Pietrovito F (2011) Trade impact of EU preferential policies: a meta-analysis of the literature. In: De Benedictis L, Salvatici L (eds), The Trade Impact of European Union Preferential Policies: An Analysis Through Gravity Models. Springer-Verlag, Berlin, Heidelberg, 91–110
Cipollina M, Salvatici L (2010) Reciprocal trade agreements in gravity models: A meta-analysis. Review of International Economics 18: 63–80
Commission for Africa (2005) Report of the Commission for Africa. report, www.commissionforafrica.info, Commission for Africa
Coulibaly S, Fontagné L (2005) South–south trade: geography matters. Journal of African Economies 15: 313–341
De P (2007) Empirical estimates of trade costs for Asia. New Delhi: Research and information system for developing countries (RIS)
De Groot HL, Poot J, Smit MJ (2009) Agglomeration externalities, innovation and regional growth: theoretical perspectives and meta-analysis. In: Capello R, Nijkamp P (eds), Handbook of Regional Growth and Development Theories. Edward Elgar, Cheltenham, 256–281
Dettmer B (2011) International service transactions: Is time a trade barrier in a connected world? Jena Economic Research Papers 2011-003, Friedrich Schiller University Jena, Jena
Disdier AC, Head K (2008) The puzzling persistence of the distance effect on bilateral trade. The Review of Economics and Statistics 90: 37–48
Dobbs R, Pohl H, Lin DY, Mischke J, Garemo N, Hexter J, Matzinger S, Palter R, Nanavatty R (2013) Infrastructure productivity: how to save $ 1 trillion a year. Instututional report, McKinsey Global Institute
Donaghy KP (2009) Regional Growth and Trade in the New Economic Geography and Other Recent Theories. Edward Elgar, Cheltenham
Doucouliagos H, Laroche P (2009) Unions and profits: A meta-regression analysis. Industrial Relations: A Journal of Economy and Society 48: 146–184
Egger M, Smith GD, Schneider M, Minder C (1997) Bias in meta-analysis detected by a simple, graphical test. The BMJ 315: 629–634
Egger P, Larch M (2008) The bilateral and multilateral trade effects of road and railway transport infrastructure. Working paper, Munich, Germany: Ifo Institute for Economic Research, Ludwig-Maximilian University of Munich
Egger PH, Lassmann A (2012) The language effect in international trade: A meta-analysis. Economics Letters 116: 221–224
Elbadawi I (1999) Can Africa Export Manufactures?: The Role of Endowment, Exchange Rates and Transaction Costs, Volume 2120. World Bank Publications, Washington DC
Elbadawi I, Mengistae T, Zeufack A (2006) Market access, supplier access, and Africa’s manufactured exports: A firm level analysis. The Journal of International Trade & Economic Development 15: 493–523
Engels EA, Schmid CH, Terrin N, Olkin I, Lau J (2000) Heterogeneity and statistical significance in meta-analysis: an empirical study of 125 meta-analyses. Statistics in Medicine 19: 1707–1728
Florax RJ, de Groot HL, De Mooij RA (2002) Meta-analysis: A tool for upgrading inputs of macroeconomic policy models. Tinbergen Institute Discussion Paper 02-041/3, Tinbergen Institute, Amsterdam
Francois J, Manchin M (2007) Institutions, infrastructure, and trade. Policy Research Working Paper Series 4152, The World Bank, Washington DC
Fujimura M, Edmonds C (2006) Impact of cross-border transport infrastructure on trade and investment in the GMS. Asian Development Bank Institute Discussion Paper 48, Asian Development Bank Institute, Tokyo
Fujita M, Krugman P, Venables AJ (1999) The Spatial Economy: Cities, Regions and International Trade. MIT Press, Cambridge, MA, London
Genc M, Gheasi M, Nijkamp P, Poot J (2012) The impact of immigration on international trade: a meta-analysis. In: Nijkamp P, Poot J, Sahin M (eds), Migration Impact Assessment: New Horizons. Edward Elgar, Northampton, MA, Chapter 9, 301–337
Geraci VJ, Prewo W (1977) Bilateral trade flows and transport costs. The Review of Economics and Statistics 59: 67–74
Glass GV (1976) Primary, secondary, and meta-analysis of research. Educational Researcher 5: 3–8
Granato M (2008) Regional export performance: First nature, agglomeration and destiny? the role of infrastructure. Mimeographed document
Grigoriou C (2007) Landlockedness, infrastructure and trade: new estimates for central Asian countries. Policy Research Working Paper Series 4335, The World Bank, Washington DC
Harbord RM, Higgins JPT (2008) Meta-regression in Stata. Stata Journal 8: 493–519
Hedges LV et al. (1992) Modeling publication selection effects in meta-analysis. Statistical Science 7: 246–255
Hernandez J, Taningco AB (2010) Behind-the-border determinants of bilateral trade flows in East Asia. Working paper 80, Asia-Pacific Research and Training Network on Trade (ARTNeT)
Holmgren J (2007) Meta-analysis of public transport demand. Transportation Research Part A: Policy and Practice 41: 1021–1035
Iwanow T, Kirkpatrick C (2007) Trade facilitation, regulatory quality and export performance. Journal of International Development 19: 735–753
Iwanow T, Kirkpatrick C (2009) Trade facilitation and manufactured exports: Is Africa different? World Development 37: 1039–1050
Jansen M, Nordås HK (2004) Institutions, trade policy and trade flows. Centre for Economic Policy Research, London
Kurmanalieva E, Parpiev Z (2008) Geography and trade in Central Asia. Research Grant Paper RO6-085, EERC
Lawless M (2010) Destinations of Irish exports: A gravity model approach. Journal of the Statistical & Social Inquiry Society of Ireland 39: 1–22
Limao N, Venables AJ (2001) Infrastructure, geographical disadvantage, transport costs, and trade. The World Bank Economic Review 15: 451–479
Longo R, Sekkat K (2004) Economic obstacles to expanding intra-African trade. World Development 32: 1309–1321
Marin D (1992) Is the export-led growth hypothesis valid for industrialized countries? The Review of Economics and Statistics: 678–688
Marquez-Ramos L, Martinez-Zarzoso I (2005) Does heterogeneity matter in the context of the gravity model? Economics Bulletin 6: 1–7
Martin P, Rogers CA (1995) Industrial location and public infrastructure. Journal of International Economics 39: 335–351
Martinez-Zarzoso I, Nowak-Lehmann F (2003) Augmented gravity model: An empirical application to MERCOSUR-European Union trade flows. Journal of Applied Economics 6: 291–316
Melo PC, Graham DJ, Noland RB (2009) A meta-analysis of estimates of urban agglomeration economies. Regional Science and Urban Economics 39: 332–342
Mundell RA (1957) International trade and factor mobility. The American Economic Review 47: 321–335
Nicoletti G, Golub S, Hajkova D, Mirza D, Yoo KY (2003) Policies and international integration: influences on trade and foreign direct investment. OECD Economics Department Working Papers 359, OECD Publishing, Paris
Nijkamp P (1986) Infrastructure and regional development: A multidimensional policy analysis. Empirical Economics 11: 1–21
Nijkamp P, Gheasi M, Rietveld P (2011) Migrants and international economic linkages: A meta-overview. Spatial Economic Analysis 6: 359–376
Nijkamp P, Poot J (2004) Meta-analysis of the effect of fiscal policies on long-run growth. European Journal of Political Economy 20: 91–124
Ninkovic J (2009) What determines export success in labor-intensive goods. In: Annual meeting of the ISAs 50th Annual Convention on “Exploring the Past, Anticipating the Future” held in New York City, Volume 15
Njinkeu D, Wilson JS, Powo Fosso B (2008) Expanding trade within Africa the impact of trade facilitation. World Bank, Washington DC
Nordas HK, Piermartini R (2004) Infrastructure and trade. WTO Staff Working Paper ERSD-2004-04, Economic Research and Statistics Division WTO, Geneva
Owyang MT, Ramey VA, Zubairy S (2013) Are government spending multipliers greater during periods of slack? Evidence from twentieth-century historical data. The American Economic Review 103: 129–134
Ozgen C, Nijkamp P, Poot J (2010) The effect of migration on income growth and convergence: Meta-analytic evidence. Papers in Regional Science 89: 537–561
Persson M (2007) Trade facilitation and the EU-ACP economic partnership agreements. Conference paper, 10th annual conference on global economic analysis
Peters JL, Sutton AJ, Jones DR, Abrams KR, Rushton L, Moreno SG (2010) Assessing publication bias in meta-analyses in the presence of between-study heterogeneity. Journal of the Royal Statistical Society: Series A (Statistics in Society) 173: 575–591
Poot J (2014) Meta-analysis of previous empirical research findings. In: Stimson RJ (ed), Handbook of Research Methods and Applications in Spatially Integrated Social Science. Edward Elgar, Cheltenham
Portugal-Perez A, Wilson JS (2012) Export performance and trade facilitation reform: hard and soft infrastructure. World Development 40: 1295–1307
Raballand G (2003) Determinants of the negative impact of being landlocked on trade: An empirical investigation through the Central Asian case. Comparative Economic Studies 45: 520–536
Ridhwan MM, De Groot HL, Nijkamp P (2010) The impact of monetary policy on economic activity: Evidence from a meta-analysis. Discussion Paper 10-043/3, Tinbergen Institute, Amsterdam
Rose AK, Stanley TD (2005) A meta-analysis of the effect of common currencies on international trade. Journal of Economic Surveys 19: 347–365
Samuelson PA (1952) The transfer problem and transport costs: The terms of trade when impediments are absent. The Economic Journal 62: 278–304
Samuelson PA (1954) The transfer problem and transport costs, ii: Analysis of effects of trade impediments. The Economic Journal 64: 264–289
Shadish WR, Haddock CK (1994) Combining estimates of effect size. In: Cooper H, Hedges LV, Valentine JC (eds), The handbook of research synthesis. Russel Sage Foundation, New York
Shepherd B, Wilson JS (2006) Road infrastructure in Europe and Central Asia: does network quality affect trade? World Bank Policy Research Working Paper 4104, The World Bank, Washington DC
Stanley TD (2005) Beyond publication bias. Journal of Economic Surveys 19: 309–345
Stanley TD, Doucouliagos C, Jarrell SB (2008) Meta-regression analysis as the socio-economics of economics research. The Journal of Socio-Economics 37: 276–292
Stanley TD, Doucouliagos H, Giles M, Heckemeyer JH, Johnston RJ, Laroche P, Nelson JP, Paldam M, Poot J, Pugh G et al. (2013) Meta-analysis of economics research reporting guidelines. Journal of Economic Surveys 27: 390–394
Stanley TD, Jarrell SB (1989) Meta-regression analysis: A quantitative method of literature surveys. Journal of Economic Surveys 19: 299–308
UN Economic Commission for Africa (UNECA) (2013) Supply-and-demand constraints to intra-Africa trade. In: UN Economic Commission for Africa (UNECA) (ed), Assessing regional integration in Africa IV. Addis Ababa, Chapter 9
Vijil M, Wagner L (2012) Does aid for trade enhance export performance? investigating the infrastructure channel. The World Economy 35: 838–868
Volpe Martincus C, Carballo J, Garcia PM, Graziano A (2014) How do transport costs affect firms’ exports? Evidence from a vanishing bridge. Economics Letters 123: 149–153
von Thünen J (1826) Der isolierte Staat in Beziehung auf Landwirtschaft und Nationalökonomie. Gustav Fischer, Jena
Wilson JS, Mann CL, Otsuki T (2004) Assessing the potential benefit of trade facilitation: A global perspective. Policy Research Working Paper Series 3224, The World Bank, Washington DC
Wu Y (2007) Export performance in China’s regional economies. Applied Economics 39: 1283–1293