 Volume
5, Number 3, 2018, 97–109 journal homepage:
region.ersa.org
Volume
5, Number 3, 2018, 97–109 journal homepage:
region.ersa.orgDOI: 10.18335/region.v5i3.223
Market Access and the Concentration of Economic
Activity in a System of Declining Cities
1 Johns Hopkins University, Baltimore, MD, USA2 The World Bank, Washington, DC, USA Received: 2 November 2017/Accepted: 16 October 2018
Abstract. While the positive effect of market access (MA) on population and economic growth has shown to be robust, the results in the literature were obtained in a context of population growth. This article examines the impact that MA has on a system of cities that has suffered a negative population shock. An extended version of the Brezis, Krugman (1997) model of life cycle of cities predicts that a system of cities experiencing population loss will see a relative reorganization of its population from small to larger cities, increasing population concentration. Accordingly, cities with higher MA will lose relatively more. We confirm these predictions using multiple definitions of MA with a comprehensive sample of cities in Eastern Europe and Central Asia, a region with declining population growth since 1990.
Key words: Market access, urban decline, demographic transition, Eastern Europe and Central Asia
1 Introduction: Market Access in a Declining System of Cities
Agglomeration economies quantify the impact on firms and worker’s incomes of being located in larger and denser local markets (Combes, Gobillon 2015). Since firms trade with distant markets, these agglomeration economies can have spillovers. The trade literature has documented that the strength of these spillovers between countries can be determined positively by the size of the economies and negatively by its trading costs, usually measured with distance (Head, Mayer 2004), following gravity models (Anderson 1979).
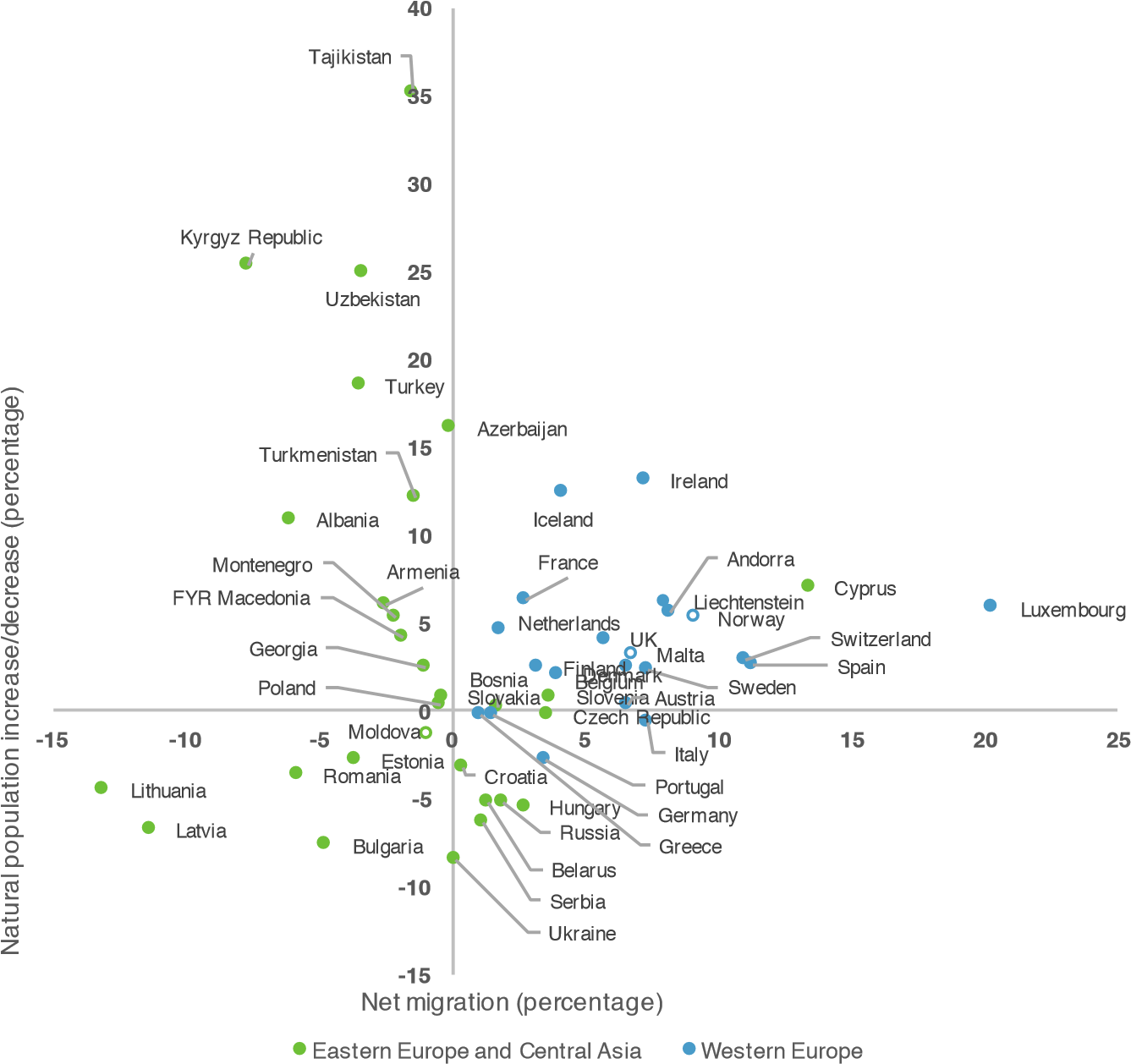
The spillovers of agglomeration economies can be measured by market access (MA), a measure that is similar to market potential, but that leaves the focus economy size out to capture the partial effect of proximity to other markets. Empirical work often follows Harris (1954) and defines trade costs as being proportional to the inverse of distance. Using a notation similar to Henderson, Wang (2007), we define city MA:
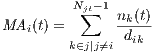 | (1) |
where n is a measure of market size1 , dik is the distance between city i and k, and Njt is the total number of cities at time t2 .
Higher MA is expected to benefit the city’s economy through higher average effective demand and average lower transportation costs for its exports to other cities. This increased demand applies to tradeable goods, but in equilibrium can affect local labor and non-tradeables. The positive effect of MA on economic output and population growth has been predominant in empirical results. Head, Mayer (2006), Bosker et al. (2010), and Combes et al. (2010) find that MA significantly increases local regional wages in different European regions. Fallah et al. (2010) find similar results for the US. These patterns have been less studied for developing economies but there are some robust results, such as Au, Henderson (2006) for China, Amiti, Cameron (2007) for Indonesia, and Quintero, Roberts (2018) for Latin America. To our knowledge, only one study has previously found a negative effect of MA (Duranton 2016).
The previous results focus on the impact of MA on productivity measured through wages. This is closely related to our analysis, but we focus instead on the effect on population growth, which is affected by differences in productivity too (Harris, Todaro 1970). Henderson, Wang (2007) and Redding, Sturm (2008) test the effect of MA precisely on population growth and find again a positive effect. Combes, Gobillon (2015) summarize estimates of MA impact and conclude that the positive effect of the economic size of distant locations and the spatial decay of this effect are rarely rejected empirically. These results have been obtained in a context of population growth. To test what would happen in the context of population decline, we perform our analysis in Eastern Europe and Central Asia, a region that has suffered a dramatic population decline in the last decades.
In contrast to most literature, we find a negative effect of MA. In a system of declining (population) cities, having a higher MA is found to be detrimental to population growth relative to the national trend. This result is robust to MA measures that use population. Alternative measures that use NLs are tested, and the results are weaker. These findings are in line with the theoretical predictions in Quintero, Restrepo (2017), which use the model found in Brezis, Krugman (1997) to simulate city population growth under the effects of a negative population shock and predict a relative reorganization of the urban population from small to larger cities. These findings highlight the importance of the insight in Glaeser, Gyourko (2005), which suggests population decline should be studied specifically and not assumed as a mirror image of positive growth.
A possible explanation for the negative impacts of MA in a declining system of cities is the effect it has on relative real income in the short run. The main prediction in Quintero, Restrepo (2017) is that a decline in population will have two main effects. First, differences in nominal wages across cities will be slow to adjust because productivity depends on historical cumulative production. Second, local costs, especially housing, will adjust downwards, creating a wedge between productivity and costs that were formerly balanced by the spatial equilibrium. This creates incentives for labor to reallocate from smaller to larger (formerly more productive) cities. In this context, MA can act as a push factor (an incentive to move out to get better pay elsewhere), as opposed to the traditional interpretation as a pull factor (an incentive to produce in a place that has access to larger markets to sell its local products).
2 Eastern Europe and Central Asia: A system of cities with declining population and increasing concentration
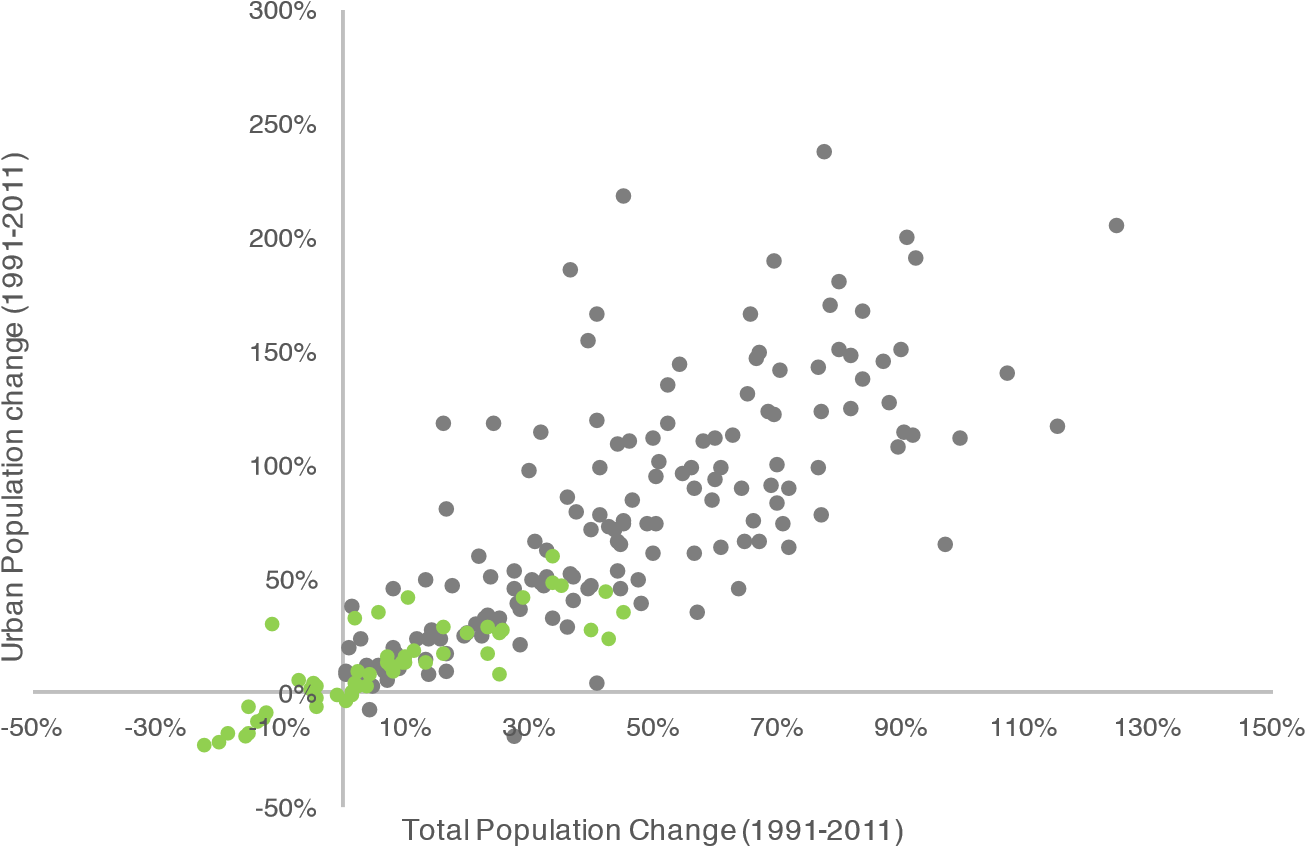
Eastern Europe and Central Asia (ECA)3 has gone through a drastic population decline. 65% of the cities lost population between 1989 and 2010, with an average loss of 21% for declining cities4 . Table 1 gives an overview of the urban systems we use in our analysis. 11 out of 15 countries present negative population growth in at least one of the decades analyzed, while the others present low positive population growth. All present a decline in growth trends observed before 1989 (see footnote 5). Decline happens all across the city size distribution, as can be seen by comparing declining cities in different size subsamples. Furthermore, the decline is happening in cities that hold an important share of the national population. Figure 1 illustrates the extent of urban population decline of countries in the ECA region compared to others in the world. In particular, this is partially explained by declining fertility rates (Table 2) that have not been offset by immigration (Figure 2).
This structural change in the population trends began at a crucial moment in the history of the region, between 1989 and 1990, when the countries in the region that had command and control economies transitioned into market economies either because of the separation of the USSR or as part of independent reform movements (the earliest transition is observed in December 1989 and the latest in March 1992). It is not surprising that many ECA cities would lose population as they transition to a market economy. Many were probably artificially large given the influences of a command economy on industry and population location prior to the transition. More freedom of movement after this transition implied actual population movement, as people left unproductive and sectoral concentrated cities, and focused on more diverse ones (Andrienko, Guriev 2004, Commander et al. 2011, Kofanov, Mikhailova 2015). Similar patterns have been studied for the rust belt in the US (Yoon 2017) and Germany (Redding, Sturm 2008).
We take this population decline as an exogenous departure point or shock in our empirical work5 . Thus, we do not attempt to further explain this shock but measure how MA affected cities heterogenous reaction to this shock.
| Country | Period | Total | Urban | % of po- | % of cities
| ||
| popula- | popula- | pulation | losing population
| ||||
| tion | tion | living in | |||||
| change | change | shrinking | |||||
| (annual) | (annual) | cities | all | >30k | >100k | ||
| Albania | 1989-2001 | -0.2 | 1.08 | 14.12 | 27.42 | 10 | 0 |
| 2001-2011 | -0.55 | 1.65 | 47.25 | 82.26 | 60 | 0 | |
| Belarus | 1989-2001 | -0.16 | 0.47 | - | - | - | - |
| 2001-2014 | -0.39 | 0.22 | 26.87 | 70.8 | 43.33 | 21.43 | |
| Bulgaria | 1989-2001 | -0.87 | -0.47 | - | - | - | - |
| 2001-2013 | -0.81 | -0.42 | 67.66 | 94.7 | 91.11 | 55.56 | |
| Georgia | 1989-2002 | -0.67 | -1.06 | 96.45 | 94.44 | 87.5 | 100 |
| 2002-2014 | 0.2 | 0.35 | 6.92 | 31.48 | 0 | 0 | |
| Kazakhstan | 1989-1999 | -0.62 | -0.68 | 59.8 | 69.86 | 67.92 | 68.18 |
| 1999-2015 | 0.85 | 0.54 | 5.8 | 21.92 | 13.21 | 0 | |
| Kyrgyz Rep. | 1989-1999 | 1.25 | 0.52 | 25.76 | 75.61 | 68 | 75 |
| 1999-2013 | 1.21 | 1.2 | 12.49 | 42.86 | 33.33 | 0 | |
| Moldova | 1989-2000 | -0.04 | -0.17 | 74.97 | 55.77 | 80 | 100 |
| 2000-2015 | -0.16 | -0.31 | 40.88 | 81.13 | 80 | 0 | |
| Poland | 1989-2003 | 0.06 | 0.13 | - | - | - | - |
| 2003-2011 | -0.04 | -0.21 | 64.06 | 52.94 | 68.21 | 82.05 | |
| Romania | 1992-2002 | -0.51 | -0.71 | 95.52 | 93.57 | 95.45 | 100 |
| 2002-2011 | -0.93 | -0.73 | 90.41 | 90.86 | 92.54 | 90 | |
| Russia | 1989-2000 | -0.01 | 0.004 | 50.15 | 65.19 | 54.51 | 50.92 |
| 2000-2010 | -0.27 | -0.23 | 42.15 | 73.61 | 63.04 | 48.17 | |
| Serbia | 1991-2002 | -0.09 | 0.43 | 50.9 | 46.37 | 55 | 60 |
| 2002-2011 | -0.36 | -0.03 | 50.94 | 71.91 | 51.28 | 11.11 | |
| Tajikistan | 1989-2000 | 1.75 | 0.02 | - | - | - | - |
| 2000-2014 | 2.05 | 2.03 | 2.38 | 5.26 | 7.69 | 0 | |
| Turkey | 1989-2000 | 1.61 | 2.73 | - | - | - | - |
| 2000-2012 | 1.31 | 2.19 | 7.77 | 59.23 | 12.77 | 4.17 | |
| Ukraine | 1989-2001 | -0.43 | -0.34 | 83.29 | 80 | 79.41 | 73.33 |
| 2001-2013 | -0.59 | -0.35 | 75.48 | 82.06 | 81.02 | 75.56 | |
| Uzbekistan | 1990-2000 | 1.87 | 1.15 | 11.88 | 10.17 | 9.84 | 22.22 |
| 2000-2014 | 1.56 | 1.33 | 5.85 | 11.86 | 8.2 | 11.11 | |
| sub-region | 1960-1989 | 1989-2000 | 2000-2014 |
| Belarus, Moldova, Ukraine, Russia | 2.25 | 1.61 | 1.36 |
| Central Europe, Baltic Countries | 2.16 | 1.54 | 1.39 |
| Central Asia | 5.12 | 3.41 | 2.74 |
| Eastern Europe, Central Asia | 2.40 | 1.72 | 1.65 |
| World | 4.26 | 2.95 | 2.54 |
Source: UN World Population Prospects
Source: UN World Population Prospects
3 Estimation of the Role of Market Access
Under this context declining population, we estimate the role of MA. We use the following estimating equation:
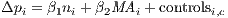 | (2) |
where Δpi is the annual percentage population change between years 2 and 3 (specified in Table 1), ni is the initial local market size, MAi is the MA defined in (1), variables are introduced in logarithms. We build controls for migration, fertility, and natural population growth rates, which vary by country c. We also control for secondary cities and groups of cities in agglomerations and include six location fundamental controls: (i) distance to border, (ii) distance to coast, (iii) forest coverage, (iv) annual precipitation, (v) average temperature in January and (vi) land usability.
Finally, to assuage any concern that the interpretation of our results which assumes a market economy for this region might be flawed, the population growth we use is calculated around 11 years after the transition, where population decline is still happening but the region’s economic systems have probably fully transitioned. Figures B.1 and B.2 shows economic indices constructed to measure, to the extent that this is possible, integration to a market economy system. The indices indicate that, at the time of our analysis, the economic systems of the countries are at least as market oriented as those of other developing regions.
3.1 Identification
We are interested in the effect of MA in the relative loss of population of cities. MA can be endogenous to population change. For instance, natural features can provide advantages that affect population growth, and at the same time affect the probability of more towns locating closer together in nearby areas, increasing MA. The endogeneity is also suggested by Hausman tests. We use instrumental variables that affect population change only through their effect on MA: a measure of city centrality calculated as the distance of each city to the center of the country; and a measurement of ranking of the city’s size within its country. These instruments perform well in a first stage, and pass Sargan’s test of overidentifying restrictions.
Our results stem from cross sectional variation: we analyze the impact of MA in the population growth of different cities exposed to the negative population shock, controlling for country effects and clustering errors at the country level. As such, unless we expect cities within the same country to adapt to a market economy at different speeds, we expect our results to be robust even in the context of different transition speeds between countries.
To further control for different cities being disproportionately affected by unobserved factors, like sectoral composition, in their transition to a market economy, we construct a dummy variable to identify places officially classified as a monotown (list obtained from Kuzmenko, Soldak 2010) in Soviet times for Russia (data only available for this country). We do not find a significant effect of this variable (these results available upon request).
3.2 Constructing Market Access Measures
| transportation costs, market size | population | NL |
| geodetic distance | MA(g,pop) | MA(g,nl) |
| driving distance | MA(d,pop) | MA(d,nl) |
We construct MA following equation (1) and restricting inclusion to cities in the same country. Table 3 shows the four versions of MA constructed: First, market size, nk(t), is measured using city population. Population is measured by each administrative unit (generally municipalities) obtained from official sources, for municipalities as small as 1,000. Despite having a shorter time frame than comparable datasets, our larger scope allows for conclusions to be applicable to the whole urban system population distribution6 .
Alternatively, we use NLs as a proxy of economic activity to capture market size. Henderson et al. (2011) discuss the benefits of using this data and present evidence of its validity as a proxy. NLs data provide a globally consistent data set that is comparable, across countries. Also, it is sampled uniformly (Henderson et al. 2012), and its measurement error is not related to development levels. Finally, NLs provide information about economic activity at levels of geographical disaggregation for which economic data is generally absent, which is the case of cities in ECA. We perform tests similar to those in Henderson et al. (2012) using subnational Gross Regional Domestic Product (GRDP) and find robust positive correlations that support the use of NLs (Table C.1).
There are two issues that affect the NL based measurements. First, the captured NL footprint, cannot be separated between municipalities whose NL emissions touch in space, forming agglomerations. We follow Roberts et al. (2015) to determine footprints and agglomerations7 and use agglomerations as our observation level when dealing with municipalities in them. Since agglomerations are groupings of cities who work as a single functional entity, we expect any type of agglomeration benefits and spillovers to be shared as well. Second, the algorithm has a lower performance when identifying dimmer NLs in smaller places. As a consequence, some smaller cities included in the total sample are left out in the sample that has NLs available data (NLs sample). The average size of the city in the NLs sample is 100,670, compared to an average population of 64,470 in the total sample. The NLs sample is nearly half the size of the total sample.
Second, we use different measures of distance as a proxy of transportation costs for exports to other cities. Most literature uses geodetic distance calculated as distance between points on an oblate spheroid (Vincenty 1975), an approximation of the earth, ignoring any actual road system8 . A more realistic measure, as suggested by Lall et al. (2004) and Combes, Gobillon (2015), is actual driving distances, which we construct using Open Source Routing Machine (OSRM) and OpenStreetMap9 .
4 Results and discussion
Table 4 shows the results of regressions of the model specified in equation 2. In the main specification that constructs MA using population, the estimated impact of MA is negative. A possible explanation for this effect is real income differences that result after a negative population shock and the effect these have in the influence of MA on population flows. The two main effects of a negative population shock discussed in Quintero, Restrepo (2017) are: First, frictions in the dynamics of productivity tend to maintain differences in nominal wages between large and small cities shortly after the shock, because productivity depends on the historical accumulation of production and knowledge. At the same time, housing prices decline in both cities due to the reduction in demand and the short run durable housing stock (Brueckner 2000). This changes the real incomes and creates incentives for labor to reallocate from smaller to larger cities (originally more productive but more expensive). The induced movement of population will be particularly strong for cities with larger MA because they have those larger, more productive, labor markets nearby for the fleeing population. Because of these income differences, and because smaller cities will have a relative higher MA10 in a fixed system of cities, this result would also predict concentration of population in fewer larger cities after a negative population shock, which is consistent with the evidence11 .
The effect after instrumentation is only significant for the MA measures that use population, not our robustness test that uses NLs. One possible explanation comes from the interpretation of the channel through which MA impacts population growth. Our results suggest that the population flow is determined by being near populated places more than being near places with large economic activity. It could be the case that it is the access to large labor markets that matters the most, as opposed to just economic activity, which could be determined more by capital in cities focused on capital intensive or extractive industries.
| MA(G,pop) | MA(D,pop) | MA(G,nl) | MA(D,nl)
| |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
| OLS | IV | OLS | IV | OLS | IV | OLS | IV | |
| local mkt | 0.034* | 0.036* | 0.034* | 0.038* | 0.002 | -0.000 | 0.003 | 0.007 |
| (13.41) | (12.97) | (13.40) | (12.42) | (0.63) | (-0.12) | (1.14) | (1.10) | |
| mkt access | -0.002 | -0.072* | -0.001 | -0.071* | -0.013* | 0.006 | -0.011* | -0.022 |
| (-0.62) | (-2.66) | (-0.37) | (-2.64) | (-2.57) | (0.31) | (-3.94) | (-1.17) | |
| nat. pop Δ | 0.007* | 0.005* | 0.007* | 0.005* | 0.009* | 0.010* | 0.010* | 0.009* |
| (16.60) | (6.68) | (16.64) | (6.13) | (12.72) | (11.28) | (13.08) | (11.92) | |
| net migration | 0.020* | 0.023* | 0.020* | 0.025* | 0.007* | 0.005 | 0.010* | 0.015+ |
| (17.72) | (13.94) | (17.54) | (11.68) | (3.16) | (1.43) | (4.17) | (1.76) | |
| Former | 0.142* | 0.097* | 0.143* | 0.101* | -0.055* | -0.045* | -0.063* | -0.075* |
| communist | (16.34) | (4.95) | (16.57) | (5.50) | (-3.20) | (-2.39) | (-3.66) | (-2.54) |
| Constant | -0.461 | 0.018 | -0.485 | -1.015 | 0.117 | 0.097+ | -0.050 | -0.200 |
| (-10.26) | (0.09) | (-10.74) | (-4.90) | (2.25) | (1.72) | (-0.78) | (-0.76) | |
| Observations | 5392 | 5381 | 5388 | 5377 | 2376 | 2368 | 2373 | 2365 |
| R2 | 0.136 | 0.070 | 0.136 | 0.060 | 0.177 | 0.170 | 0.180 | 0.174 |
| Adjusted R2 | 0.135 | 0.068 | 0.135 | 0.059 | 0.174 | 0.167 | 0.177 | 0.170 |
Another possible interpretation of the difference in the results could come from the changes in the sample of cities used (see discussion in Section 3.2). The NLs sample of cities is smaller and concentrated in larger cities. If the negative effect of MA is mainly led by smaller cities, then our measurement of MA with NLs would not be appropriate, and we should rely on the population-based measurements. This result is in agreement with Greenstone et al. (2010), which discusses that the effect of MA is larger for smaller cities because they rely more on outside markets. Yet, results are robust to using either geodetic distance or driving distance, which makes the former preferable for this application given its much lower cost to calculate.
The role of local market size changes significantly when using measures with NLs and population. In specifications 1-4 a larger local market is associated with lower population loss, as predicted in the Brezis, Krugman (1997) model. The effect is not significant for the MA measure that uses NLs. As before, it could be the case that either local agglomeration economies are led by population size and not the magnitude of the economy, or that the effects are different because of sample selection implied by the nature of NL measurement. Finally, the effect of belonging to a formerly communist country is also different in the different specifications. Cities in former communist countries lost, on average, more population when considering the NLs sample, which could be again driven by sample selection. Other variables included have the expected values.
In conclusion, we present evidence suggesting that having higher MA – when operating in an environment of population decline – is detrimental to city population growth. The impact is negative for the MA measure that uses population as a proxy for market size, our preferred specification. We use a comprehensive sample of cities in Eastern Europe and Central Asia, which allows us to capture the effect on cities in all ranges of the city size distribution. Even in countries where all cities are losing population, this result suggests that cities with higher MA would lose relatively more. Our results contrast with the positive effects of MA found in the literature, which are estimated in a context of population growth. In times of population decline, nearby large markets could instead act as a push factor, as the remaining population see them as possible labor markets.
Future work should analyze the heterogeneity of the effects in cities of different sizes. Evaluating the causal impact of local market sizes in a context of decline is another interesting area to elaborate on the results of this letter.
References
Amiti M, Cameron L (2007) Economic geography and wages. The Review of Economics and Statistics 89[1]: 15–29. CrossRef.
Anderson JE (1979) A theoretical foundation for the gravity equation. The American Economic Review 69[1]: 106–116
Andrienko Y, Guriev S (2004) Determinants of interregional mobility in Russia. Economics of transition 12[1]: 1–27. CrossRef.
Au CC, Henderson JV (2006) Are Chinese cities too small? The Review of Economic Studies 73[3]: 549–576. CrossRef.
Bosker M, Brakman S, Garretsen H, Schramm M (2010) Adding geography to the new economic geography: Bridging the gap between theory and empirics. Journal of Economic Geography 10[6]: 793–823. CrossRef.
Brezis ES, Krugman PR (1997) Technology and the life cycle of cities. Journal of Economic Growth 2[4]: 369–383. CrossRef.
Brueckner JK (2000) Urban growth models with durable housing: An overview. In: Huriot JM, Thisse J (eds), Economics of Cities: Theoretical Perspectives. Cambridge University Press, Cambridge, 263–289
Combes PP, Duranton G, Gobillon L, Roux S (2010) Estimating agglomeration economies with history, geology, and worker effects. In: Glaeser E (ed), Agglomeration economics. University of Chicago Press, Chicago IL. CrossRef.
Combes PP, Gobillon L (2015) The empirics of agglomeration economies. In: Duranton G, Henderson V, Strange W (eds), Handbook of Regional and Urban Economics, Volume 5. Elsevier, Oxford
Commander SJ, Nikoloski Z, Plekhanov A (2011) Employment concentration and resource allocation: One-company towns in Russia. European Bank for Reconstruction and Development
Duranton G (2016) Agglomeration effects in Colombia. Journal of Regional Science 56[2]: 210–238. CrossRef.
Fallah BN, Partridge MD, Olfert MR (2010) New economic geography and US metropolitan wage inequality. Journal of Economic Geography 11[5]: 865–895. CrossRef.
Fujita M, Krugman PR, Venables AJ (1999) The spatial economy: Cities, regions and international trade. The MIT Press, Cambridge, MA. CrossRef.
Gendron-Carrier N, Gonzalez-Navarro M, Polloni S, Turner MA (2017) Subways and urban air pollution. NBER working paper series, working paper 24183. CrossRef.
Glaeser EL, Gyourko J (2005) Urban decline and durable housing. Journal of Political Economy 113[2]: 345–375. CrossRef.
Greenstone M, Hornbeck R, Moretti E (2010) Identifying agglomeration spillovers: Evidence from winners and losers of large plant openings. Journal of Political Economy 118[3]: 536–598. CrossRef.
Harris CD (1954) The market as a factor in the localization of industry in the United States. Annals of the association of American geographers 44[4]: 315–348. CrossRef.
Harris JR, Todaro MP (1970) Migration, unemployment and development: A two-sector analysis. The American Economic Review 60[1]: 126–142
Head K, Mayer T (2004) The empirics of agglomeration and trade. In: Henderson J, Thisse JF (eds), Handbook of Regional and Urban Economics, Volume 4. North Holland, Amsterdam, 2609–2669
Head K, Mayer T (2006) Regional wage and employment responses to market potential in the EU. Regional Science and Urban Economics 36[5]: 573–594. CrossRef.
Henderson JV, Wang HG (2007) Urbanization and city growth: The role of institutions. Regional Science and Urban Economics 37[3]: 283–313. CrossRef.
Henderson V, Storeygard A, Weil D (2011) A bright idea for measuring economic growth. The American Economic Review: Papers and Proceedings 101[3]: 194–199. CrossRef.
Henderson V, Storeygard A, Weil D (2012) Measuring economic growth from outer spaces. The American Economic Review 102[2]: 994–1028. CrossRef.
Kofanov D, Mikhailova T (2015) Geographical concentration of Soviet industries: A comparative analysis. Journal of the New Economic Association 28[4]: 112–141
Kuzmenko L, Soldak M (2010) Monofunctional cities: Problems, support provision and development. Економiчний вiсник Донбасу 4: 83–88
Lall SV, Shalizi Z, Deichmann U (2004) Agglomeration economies and productivity in Indian industry. Journal of Development Economics 73[2]: 643–673. CrossRef.
Quintero L, Restrepo P (2017) City decline in an urbanizing world. Available from the authors upon request
Quintero L, Roberts M (2018) Explaining spatial variations in productivity: Evidence from Latin America and the Caribbean. The world bank. CrossRef.
Redding SJ, Sturm DM (2008) The costs of remoteness: Evidence from German division and reunification. The American Economic Review 98[5]: 1766–1797. CrossRef.
Roberts M, Stewart B, Prakash M, McWilliams K (2015) Global night time lights urban extents and growth patterns product. Alpha Version World Bank
The Heritage Foundation (2018) Index of economic freedom. Technical report
The World Bank (2018) Ease of doing business index. Technical report. CrossRef.
Vincenty T (1975) Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Survey review 23[176]: 88–93. CrossRef.
Yoon C (2017) Estimating a dynamic spatial equilibrium model to evaluate the welfare implications of regional adjustment processes: The decline of the rust belt. International Economic Review 58[2]: 473–497. CrossRef.
A Concentration
Besides population decline, the region has presented concentration of population in fewer larger cities, which is precisely the prediction of Brezis, Krugman (1997) as a response to such a negative population shock. GINI coefficients for most ECA countries in table 5, for both population and night lights (NLs), support this. Only two countries show decreases in the population concentration, and the average growth in concentration is 0.51% per year overall.
| Population GINI | Change | NLs GINI | Change
| |||||||
| year 1 | year 2 | year 3 | year 1 | year2 | year 3 | |||||
| Serbia | 0.507 | 0.507 | 0.7 | + | 1.81% | 0.564 | 0.558 | 0.785 | + | 1.87% |
| Kazakhstan | 0.508 | 0.542 | 0.651 | + | 1.34% | 0.64 | 0.725 | 0.739 | + | 0.74% |
| Russia | 0.608 | 0.629 | 0.758 | + | 1.17% | 0.756 | 0.795 | 0.834 | + | 0.49% |
| Bulgaria | 0.628 | 0.68 | + | 0.83% | 0.768 | 0.776 | 0.782 | + | 0.09% | |
| Belarus | 0.668 | 0.713 | + | 0.67% | 0.831 | 0.837 | 0.804 | – | -0.15% | |
| Albania | 0.696 | 0.718 | 0.756 | + | 0.41% | 0.77 | 0.783 | 0.814 | + | 0.27% |
| Poland | 0.712 | 0.735 | + | 0.32% | 0.854 | 0.856 | 0.799 | – | -0.31% | |
| Tajikistan | 0.61 | 0.629 | + | 0.31% | 0.671 | 0.706 | 0.796 | + | 0.89% | |
| Moldova | 0.656 | 0.708 | 0.688 | + | 0.23% | 0.775 | 0.768 | 0.787 | + | 0.07% |
| Kyrgyz Rep. | 0.644 | 0.676 | 0.671 | + | 0.20% | 0.799 | 0.797 | 0.811 | + | 0.07% |
| Romania | 0.622 | 0.63 | 0.641 | + | 0.15% | 0.679 | 0.695 | 0.685 | + | 0.04% |
| Ukraine | 0.737 | 0.735 | 0.744 | + | 0.05% | 0.834 | 0.891 | 0.814 | – | -0.11% |
| Uzbekistan | 0.674 | 0.652 | 0.65 | – | -0.17% | 0.826 | 0.817 | 0.82 | – | -0.03% |
| Georgia | 0.674 | 0.672 | 0.64 | – | -0.24% | 0.709 | 0.763 | 0.774 | + | 0.44% |
B Transition to Market Economies
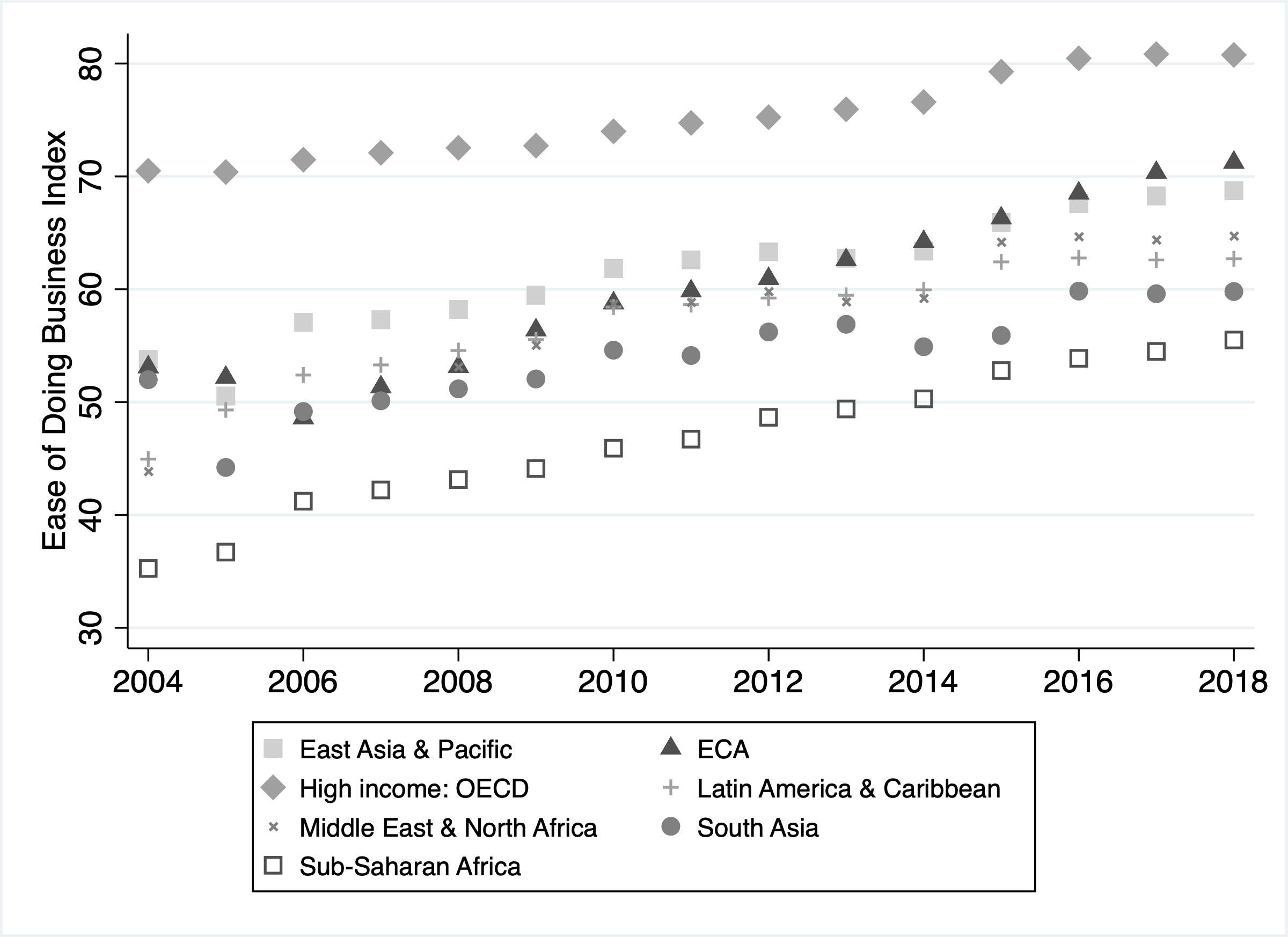
Notes: The Economic Freedom Index measures how economically free societies are, where freedom is understood
as no government obstruction to the free movement of labor, capital, and goods (The Heritage
Foundation 2018)
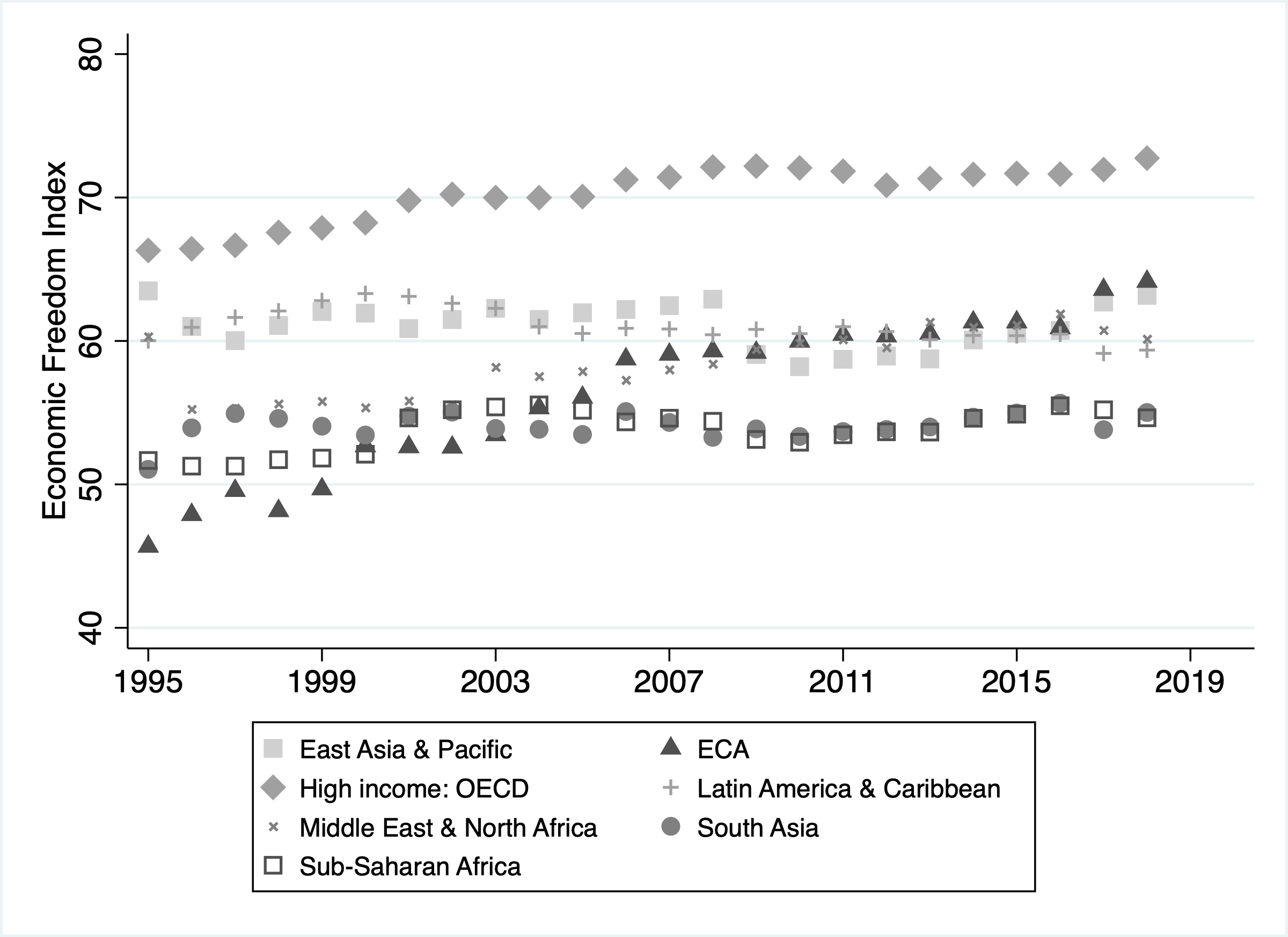
Notes: The Ease of Doing Business Index measures how fair and friendly economies are to medium and small
private firms (The World Bank 2018)
C Using NLs as a proxy of economic activity
| Country | Log NLs | Constant | Observations | R2 | ||
| Albania | 1.24 | ** | -0.48 | 12 | 0.80 | |
| Belarus | 1.25 | ** | -6.43 | 6 | 0.84 | |
| Bulgaria | 1.17 | *** | -6.04 | *** | 140 | 0.72 |
| Georgia | 0.88 | * | -1.19 | 7 | 0.6 | |
| Germany | 0.72 | *** | 0.95 | *** | 1,980 | 0.41 |
| Kazakhstan* | 0.50 | ** | 21.20 | *** | 28 | 0.13 |
| Kyrgyz Republic | 0.92 | *** | 0.21 | 7 | 0.66 | |
| Poland | 0.61 | *** | 0.87 | *** | 325 | 0.94 |
| Romania | 1.07 | *** | -4.92 | *** | 210 | 0.67 |
| Russia | 0.33 | *** | 6.82 | *** | 456 | 0.98 |
| Serbia* | 1.26 | *** | -1.87 | 25 | 0.83 | |
| Tajikistan* | 0.92 | *** | 13.17 | *** | 8 | 0.99 |
| Turkey | 1.40 | *** | 0.21 | 52 | 0.74 | |
| UK | 0.56 | *** | 2.56 | *** | 840 | 0.28 |
| Ukraine* | 0.85 | *** | -0.69 | 135 | 0.5 | |
| Uzbekistan | 1.01 | *** | 1.94 | 39 | 0.95 | |
 © 2019 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
© 2019 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)