Volume
5, Number 1, 2018, 17–32 journal homepage:
region.ersa.org
Volume
5, Number 1, 2018, 17–32 journal homepage:
region.ersa.orgDOI: 10.18335/region.v5i1.190
An Index to Characterize the Multi-Dimensional Nature of Land Use Regulations in the Greater Houston Metropolitan Area
1 St. Cloud State University, St. Cloud, MN, USA Received: 23 March 2017/Accepted: 13 January 2018Abstract. Although housing prices and the lack of real income growth are cited as the main factors behind the housing affordability problem, it has been proven that land use regulations have some responsibility as well. Indexes have been the most common indicator used to characterize the stringency of local land use regulations; however, these studies focus primarily on those most stringent regulatory environments, and therefore there is no evidence of the validity of such indexes in areas regarded as less stringent. In response to this lack of evidence, using a unique data set, this article presents an index characterizing local regulatory environments in a well-known less stringent regulatory environment: the Houston-Galveston Area in Texas. This index proves to be a robust measure capable of capturing the multi-dimensional nature of land use regulations. The analysis and validation of the index confirms the importance of the use of these composite measures to characterize land use regulatory environments of metropolitan areas.
Key words: Land use regulations, affordable housing, index
1 Introduction
Studies suggest that stringent land use regulatory environments (LUREs, hereafter) exacerbate the problem of affordable housing. Although this effect is clearer in Metropolitan Statistical Areas (MSA) with stringent regulatory environments, it is also present in other MSAs with less stringent regulations. For instance, Texas is among the states whose metropolitan areas have been considered as less stringent in terms of its LUREs (Pendall et al. 2006, Gyourko et al. 2008). Additionally, even if the impact on affordable housing is not clear, other related problems such as segregation could be strongly related to the type of land and development regulations in place (Quigley, Rosenthal 2005).
Analysis regarding the effect of land use regulations on housing markets is abundant. However, most of these studies are limited to the study of the effect of one specific regulation (e.g., growth boundaries, impact fees), failing to consider the multi-dimensional nature of land use regulations and the accompanying consequences (Cutsinger et al. 2005). Only a few studies look at the multi-dimensional nature of LUREs and their effect on residential markets (Knaap 1998, Quigley, Rosenthal 2005).
The attempt to study the overall effect of LUREs is complex. To do this, most studies have relied on the creation of an index that could capture the different dimensions involved. Any effort to create such an index requires that all regulations present in local jurisdictions be considered. Thus, the first challenge that these studies should overcome is to obtain an inventory of land use regulations in each jurisdiction being analyzed.
Surveys to obtain data on local land use regulations have been conducted by authors and institutions such as Black, Hoben (1985); the Wharton Project (Linneman et al. 1990); Pendall et al. (2006); Gyourko et al. (2008); Glickfeld, Levine (1992); Lewis, Neiman (2000); The Pioneer and Rappaport Institute (Dain 2006), and Ihlanfeldt (2007). Most of the indexes created with this data have been conducted in LUREs known to be stringent (e.g. California, Florida, Massachusetts), which raises questions about whether generalizations based on such results can be accurate (Green 2009, Malpezzi 2009).
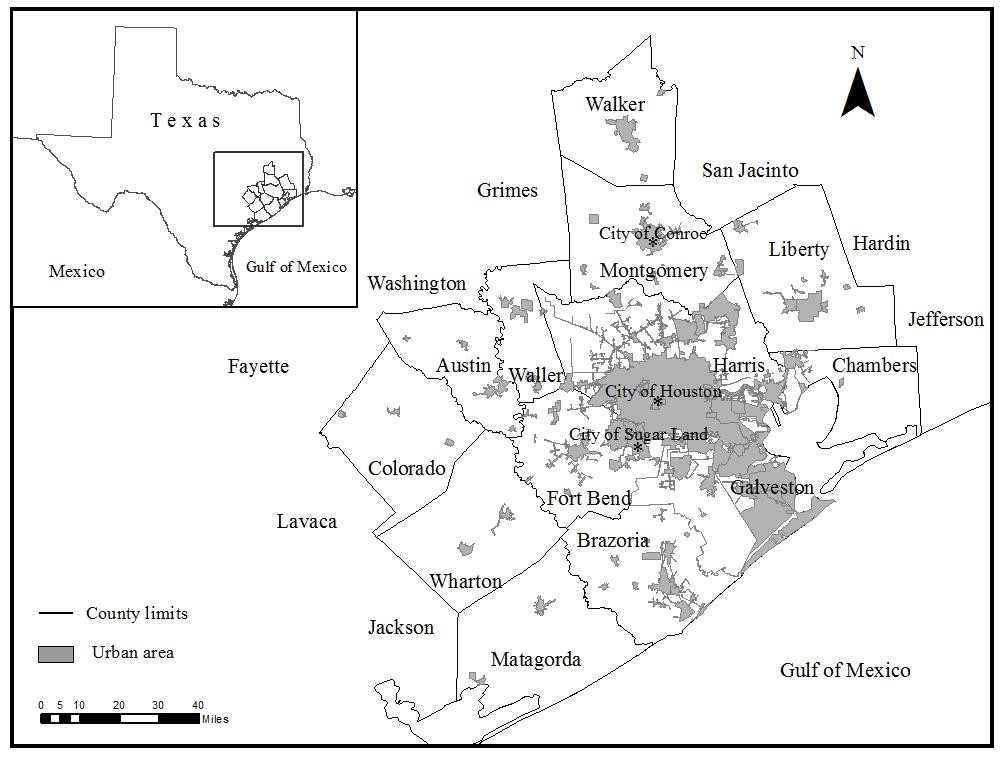
Based on previous studies and the limitations which have been observed, the main question driving this paper is whether an index of land use regulatory stringency could be a valid measure to characterize regulatory environments for housing markets in other geographies with less stringent regulatory environments. To answer this question, an index is created to reflect the different LUREs in the Houston–Galveston Area in Texas (H-GA, hereafter). Houston’s lack of zoning ordinance makes this region a unique case study to contribute to the literature by creating an index characterizing LUREs for housing markets. However, the lack of zoning in Houston does not mean that there are no other types of land use regulations in place. Deed restrictions (covenants) are the most common type of land use regulations in the city. The H-GA is defined by the 13 counties which are part of the Houston-Galveston Area Council (see Figure 1).
The plan of the article is as follows: The data and methodology section describe the survey instrument and the methodological process of creating the LURE index. The following section describes in detail the process of the creation of the LURE index and its sub-indexes and the rankings of jurisdiction. The final section presents the analysis and validation of the index through statistical correlations with local traits and comparison with a second alternative. There is a summary and statement of general conclusions.
2 Literature review
Composite indicator, index, performance indicator, and rating scale are some of the different terms frequently used to describe a measure that expresses the final rating based on a measure created by either using a single or multiple items or attributes. For the purposes of this research, and because similar approaches and methodologies are used in comparable exercises and fields, the terms Composite Indicator (CI) and Index (I) are alternatively used to describe the measurement used to characterize multi-dimensional phenomena. Indexes are commonly found in the economic, social, health, and policy fields (Freudenberg 2003). The uniqueness of having a measure to characterize multi-dimensional phenomena makes them a useful tool. Some of the ways in which these fields make use of indexes is to create a ranking using this measure and then to measure performance or to rank countries or institutions. For instance, up until 2008, there were 178 CIs ranking country performances based on economic, political, social, or environmental measures (Bandura 2008).
Indexes are popular because of their capacity to characterize complex phenomena. The multi- dimensional aspects of some constructs make them difficult to grasp at first glance, so indexes are useful in providing a single measure to capture the totality of such phenomena (Nunnally 1978).
A fundamental part of the construction of a statistically sound and consistent index is the appropriate definitions of dimensions that the index is intended to measure. Literature review and the opinion of experts and stakeholders are essential to select the appropriate framework with variables that could fulfill the required dimensions.
The literature review provided: 1) a general array and classification of different variables related to land use regulations; 2) a detailed review of the studies creating inventories of land use regulations and studies creating LURE indexes; and 3) a list of candidate variables that was used in the creation of the LURE index.
The creation of LURE indexes has relied on inventories of land use regulations from which candidate variables have been selected. Most of the indexes were either created based on already existing databases of land use regulations (Glaeser, Ward 2009, Malpezzi 1996, Quigley, Raphael 2005, Somerville 1999) or by creating an inventory of land use regulations first and then crafting an index (Black, Hoben 1985, Gyourko et al. 2008, Ihlanfeldt 2007, Pendall et al. 2006, Segal, Srinivasan 1985).
Studies creating an inventory of land use regulations have relied on the implementation of a survey directed (in most of the cases) towards the jurisdiction’s planning staff (Black, Hoben 1985, Dain 2006, Glickfeld, Levine 1992, Gyourko et al. 2008, Ihlanfeldt 2007, Lewis, Neiman 2000, Linneman et al. 1990, Pendall et al. 2006).
Of all the inventories which were reviewed, the ones of the Wharton Urban Decentralization Project (Linneman et al. 1990) and Glickfeld, Levine (1992) probably have been the most frequently used by other studies in the creation of indexes. Other inventories used were those from institutions such as the American Institute of Planners (AIP 1976), the National Multi Housing Council (NMHC 1982), the Urban Land Institute 1980-81 (Black, Hoben 1985), the US Department of Housing and Urban Development (HUD 1991), Lewis, Neiman (2000) and the Pioneer Institute for Public Policy Research and Harvard’s Rappaport Institute for Greater Boston (Glaeser, Ward 2009).
The geographical coverage of each of these studies was different. Some were defined on a national level and the surveys were sent to either all municipalities in the U.S. (Gyourko et al. 2008, Linneman et al. 1990) or were limited to local governments in specific MSAs (Black, Hoben 1985, Pendall et al. 2006, Segal, Srinivasan 1985). Others surveyed jurisdictions at the state level (Glickfeld, Levine 1992, Ihlanfeldt 2007, Lewis, Neiman 2000).
The goals for creating an index were different in every study. Some were investigating the effect of regulations on: a) land prices, housing, and rent costs (Black, Hoben 1985, Ihlanfeldt 2007, Malpezzi 1996, Segal, Srinivasan 1985); b) concentration of homebuilders (Somerville 1999); and c) supply and price (or rent) of housing (Quigley, Raphael 2005). In other cases, the goal was to create an index in order to characterize regulatory environments based on their stringency (Gyourko et al. 2008, Pendall et al. 2006).
Some studies were particularly interested in creating an index which took into account a certain amount of specific regulations, such as growth control measures, minimum lot sizes, etc. (e.g. Malpezzi 1996, Glaeser, Ward 2009), while others were interested in creating an index that would reflect the overall multi-dimensional nature of land use regulations (Pendall et al. 2006, Gyourko et al. 2008).
In terms of the specific methodology in the creation of indexes, studies have relied on the simple addition method (linear arithmetic addition) for aggregation and either equal or factor analysis approaches for weighting. In relation to the last two options, some studies claimed not to find significant differences in their results when using either one of these methods (e.g. Gyourko et al. 2008).
Among all these studies, the one done by Gyourko et al. (2008) deserves special mention. This study offered detailed information regarding the methodological process used in creating their index. Details such as normalization, aggregation, weighting and imputation procedures were clearly explained.
The creation of the LURE index had to take these methodological aspects into account to allow for the possibility of comparison with these other reviewed exercises. This information was also helpful in establishing a sound framework as the first step in creating the LURE index.
3 Data and methodology
Data on regulations for the H-GA comes from an instrument created to identify land use regulations related to housing markets. It was created with the intention of being simple enough to generate relevant information and be easily implemented on a regular basis. The design process was based on a multi-methodological approach: a) using surveys from studies which have developed these types of inventories; and b) interviews with different experts and stakeholders in Texas (city planning officials, housing developers, and law experts).
The survey was sent to the planning directors of the areas where such an office existed. In the areas where there was no planning director, the survey was sent to either a local elected official (e.g., mayor, planning board chair, city clerk) or a municipal officer (e.g., city manager, city engineer). All 133 jurisdictions of the H-GA received the LURE survey. No random sample was selected.
Once missing and extreme values were analyzed, verified, and corrected, the information was used in the creation of the LURE index. Specific methodological and implementation details of the survey can be found in Estevez Jimenez (2012).
3.1 Methodology
The methodology for the creation of the LURE index was designed in order to ensure a top-quality indicator in terms of its statistical soundness and consistency. The methodology allowed that the index would include assessments following the requirements for measures in psychometric theory: validity, reliability and sensitivity to change (Nunnally 1978, Nunnally, Bernstein 1994). The methodological steps were: 1) definition of the framework; 2) imputation process; 3) creation of sub-indexes by simple addition of values; 4) assessment of the statistical dimensionality of the framework by Principal Component Analysis (PCA); 5) normalization of sub-indexes through standardized scores; 6) definition of weights for the aggregation through FA/PCA analysis; and 7) aggregation by simple addition. Following is a brief description of these steps.
The LURE index is defined by 10 sub-indexes and 29 indicators, which were considered sufficient to capture the different dimensions characterizing the H-GA’s LURE. Because the Gyourko et al. (2008) index is a well-created composite indicator as far as methodology, the conceptual framework and specific procedures selected for the creation of the LURE index follow the same approach. Nine of the ten sub-indexes are similar to those created by Gyourko et al. (2008). Table 1 shows the 10 sub-indexes, the indicators and their coding, and score units. The sub-index Local Government is the only new addition in the creation of the LURE index. Experts and stakeholders interviewed recommended the inclusion of this particular indicator due to its relevance for Texas jurisdictions.
|
Sub-Indexes |
score
| |||
| Indicator (Variable) | code | permitted | unit | |
| values | ||||
| Local Government (LGI) | ||||
| Category of Municipality | LGIgeneral | 0 or 1 | GL/HRa | |
| Local Planning Approval (LPAI) | ||||
| Zoning commission | LPAIzc | 0 or 1b | Board | |
| Planning commission | LPAIpc | 0 or 1b | Board | |
| Historic commission | LPAIhc | 0 or 1b | Board | |
| Board of adjustments | LPAIba | 0 or 1b | Board | |
| Neighborhood zoning areas | LPAInza | 0 or 1b | Board | |
| Local Planning Requirement (LPAIR) | ||||
| Comprehensive (master, general) plan | LPAIcp | 0/1/2c | Document | |
| Zoning ordinance | LPAIzo | 0/1/2c | Document | |
| Other ordinances governing plats, land development and subdivisions | LPAIoo | 0/1/2c | Document | |
| Jurisdiction is a unit in which the county applies its own subdivision provisions to new development | LPAIosp | 0or 1b | Yes or No | |
| Local Affordable Housing (LAHI) | ||||
| Multifamily housing units have been built in the last two years | LAHImh | 0 or 1b | Yes or No | |
| Manufactured and modular housing have been added to jurisdiction in the last two years | LAHImm | 0or 1b | Yes or No | |
| Developers have to include “affordable housing” (however defined) | LAHIah | 0 or 1b | Yes or No | |
| Density Restriction (DRI) | ||||
| Minimum lot size for single family units within the city limits | DRImlsfu | 0< | Sq. ft. | |
| Minimum lot size for single family units within the city’s extraterritorial jurisdiction (ETJ) | DRImlsfuetj | 0< | Sq. ft. | |
| Minimum floor area for single family units within the city limits | DRImfasfu | 0< | Sq. ft. | |
| Local Subdivision Requirements (LSR) | ||||
| Developers have to pay building permit fee | LSRIbpf | 0 or 1b | Yes or No | |
| Developers have to pay development review fees | LSRIdrf | 0 or 1b | Yes or No | |
| Open Space (OSI) | ||||
| Developers have to supply mandatory dedication of space or open space (or fee in lieu of dedication) | OSI | 0 or 1b | Yes or No | |
| Exactions (EI) | ||||
| Developers have to pay allocable share of costs of infrastructure improvement | EI | 0or 1b | Yes or No | |
| Supply Restriction (SRI) | ||||
| Measure limiting development beyond a boundary (such as urban limit line, urban growth boundary, greenbelt, or urban service area) | ||||
| SRIc | 0 or 1b | Yes or No | ||
| Measure establishing a limit on growth (population limit or building permits in a given time frame) | SRIgc | 0 or 1b | Yes or No | |
| Measure which requires adequate service levels for residential development or service capacity as a condition of approval of residential development | ||||
| SRIir | 0 or 1b | Yes or No | ||
| Measure which reduces the permitted residential density by general planning or rezoning | SRIpd | 0 or 1b | Yes or No | |
| Measure which re-designates or rezones residential land to agriculture or open space (e.g., shore line protection) | SRIr | 0 or 1b | Yes or No | |
| Local Standard Development Perception (LSDPI) | ||||
| Perception of jurisdiction’s standards for development when compared to surrounding jurisdictions | LSDPIsj | 0/1/2d | See note c | |
| Perception of jurisdiction’s standards for development when compared to county | LSDPIc | 0/1/2d | See note d | |
The Multiple Imputation Procedure (MI) was the technique utilized based on the pattern of missing values and the presence of some extreme values in the dataset. From the 27 variables, just two were not considered in the estimation of missing values because they were not found to have any missing information. The iterative Markov Chain Monte Carlo (MCMC) method was the best suited for the MI procedure. Scale variables were modeled through linear regression and categorical variables with a logistic regression. The accuracy of the MI modeling was checked by: a) verifying the presence of negative and out-of-bound values, and b) by assessing the model convergence.
Multivariate Analysis (MA) allowed for the verification of adequate correspondence between the theoretical structure (depicted by the different dimensions/sub-indexes and indicators in the framework) established before the creation of the H-GA’s land use regulations inventory and the statistical structure seen in the collected data. Factor Analysis (FA) was carried out to confirm the number of dimensions/sub-indexes (components).
FA was performed involving: 1) computation of correlation matrix (small partial correlation coefficients are a desired effect to perform FA); 2) extraction of factors (components); and 3) rotation of factors. All correlation coefficients among the sub-indexes were small, which is a good indicator that the different sub-indexes are not highly correlated. Therefore, it is clear that the ten dimensions/sub-indexes established in advance accurately capture the different aspects of the H- GA LURE and its effect on housing markets. The fact that five dimensions account for almost 65% of the variance shows that the effect of LUREs on housing markets is indeed a multi- dimensional phenomenon. (In this instance, it is not considered necessary for a few factors to explain as much variance as possible.)
In order to compare the LURE index with other similar composite indicators, a normalization of the ten sub-indexes was performed. The standard deviation from the mean procedure (Z-score) was the approach selected to create the LURE index.
The Z-score procedure was defined as:
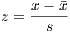
Where z is the standard score, x the actual value, the mean value of the actual values, and s the corresponding standard deviation.
FA was the technique selected for the weighting of the ten sub-indexes of the LURE index because it is the most common method used in other similar LURE indexes. The linear aggregation method (weighted mean or arithmetic average) was used to create the LURE index. Linear aggregation’s properties made it suitable for the characteristics of the dataset of the LURE index.
The linear aggregation used to create the LURE index is defined:
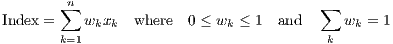
Table 2 shows an example of the calculation of the index for the City of Roman Forest:
| Subindexes | LGI | LPAI | LPAIR | LAHI | DRI | LSRI | OSI | EI | SRI | LSDPI | Index |
| FA weights | .09 | .04 | .05 | .16 | .24 | .07 | .12 | .04 | .11 | .08 | |
| Z-score | -.86 | .80 | .99 | -.18 | 3.35 | .69 | .86 | .70 | -.35 | 1.26 | |
| -.08 | .03 | .05 | -.03 | .80 | .05 | .10 | .03 | -.04 | .10 | 1.02 | |
4 The LURE index and its ten sub-indexes
The creation of the sub-indexes was a straightforward process because most of the score units for the indicators were the same. There was no need for the normalization of values. The advantage of this approach is that the richness of the values is preserved (Nardo et al. 2004).
4.1 Sub-index descriptions
- Local Government Sub-Index (LGI). Only the variable “category of municipality”
defined this sub- index. If a municipality is a home rule jurisdiction, then a value
of 1 is received. If general law is the answer, then a value of zero is recorded.
It is assumed that the ability of home rule jurisdictions to implement their own
regulations allows them to have a more direct effect on housing markets, as opposed
to general law jurisdictions.
Home Rule = 1 General = 0
- Local Planning Approval (LPAI). Five items are used to create this sub-index.
Jurisdictions are asked if they have a: 1) zoning commission (LPAIzc); 2) planning
commission (LPAIpc); 3) historic commission (LPAIhc); 4) board of adjustments
(LPAIba); and 5) neighborhood zoning areas (LPAInza).
Whenever the response is a “yes” regarding any of those entities, a score of “1” is received. The assumption is that the more entities involved in the regulatory process, the greater the impact on housing markets. The LPAI sub-index could be summarized as:
LPAI = LPAIzc + LPAIpc + LPAIhc + LPAIba + LPAInza
- Local Planning Approval Requirement (LPAIR). The LPAIR sub-index is formulated
based on answers to questions about the existence in jurisdictions of: 1)
comprehensive (master, general) plan (LPAIcp); 2) zoning ordinance (LPAIzo); and
3) other ordinances governing plats, land development and subdivisions (LPAIoo);
and if the jurisdiction is a unit in which the county applied its own subdivision
provisions to new developments (LPAIosp).
LPAIR = LPAIcp + LPAIzo + LPAIoo + LPAIosp
- Local Affordable Housing (LAHI). This sub-index is based on answers to questions about
whether: multifamily housing units have been built in the last two years (LAHImh);
manufactured and modular housing have been added to the jurisdiction in the last
two years (LAHImm); and if developers are required to include “affordable housing”
(LAHIah).
LAHI = LAHImh + LAHImm + LAHIah
This is the only case where responses of “no” added a value of 1 to the sub-index. The assumption is that communities not adding either multifamily or manufactured housing to their development are likely restricting the production of affordable housing.
- Density Restriction (DRI). Three questions are used for this sub-index: minimum lot
size for single family units within the city limits (nlDRImlsfu); minimum lot sizes
for single family units within the city’s extraterritorial jurisdiction (nlDRImlsfuetj);
and minimum floor area for single family units within the city limits (nlDRImfasfu).
DRI =nlDRImlsfu + nlDRImlsfuetj + nlDRImfasfu
- Local Subdivision Requirements (LSRI). The LSRI sub-index is created from questions
about if developers must pay building permit fees (LSRIbpf) and if developers must
pay development review fees (LSRIdrf).
LSRI = LSRIbpf + LSRIdrf
- Open Space (OSI). This sub-index simply uses one item: whether developers have to provide mandatory dedication of space or open space. OSI could be stated as having a value of 1 if there is a “yes” answer and 0 otherwise.
- Exactions (EI). The EI sub-index is formulated based on whether developers have to pay an allocable share of costs of infrastructure improvement. The index received a 1 if “yes” is the answer and 0 if “no” is the answer.
- Supply Restriction (SRI). This sub-index is generated by the answers to whether the
jurisdiction has any: measure limiting development beyond a boundary (SRIc);
measure establishing a limit on growth (SRIgc); measure which requires adequate
service levels for residential development or service capacity as a condition of
approval of residential development (SRIir); measure which reduces the permitted
residential density by general planning or rezoning (SRIpd); or measure which
re-designates or rezones residential land to agriculture or open space (SRIr). For
any “yes” response in any of these measures a value of 1 is given.
SRI = SRIc + SRIgc + SRIir + SRIpd + SRIr.
- Local Standard Development Perception (LSDPI). Two items are used to create the
LSDPI sub- index: 1) perception of a jurisdiction’s standards for development
when compared to surrounding jurisdictions (LSDPIsj); and 2) perception of a
jurisdiction’s standards for development when compared to the county (LSDPIc).
LSDPI = LSDPIsj + LSDPIc
This is the only sub-index in which the values ranged from 0 to 2 because the possible answers for these questions are 0 for lower standards, 1 for comparable standards, and 2 for higher standards.
4.2 LURE index ranking results
Table 3 shows the LURE index values and rankings obtained for each one of the 91 jurisdictions. The interpretation of the index is straightforward. High values (positive) mean that those jurisdictions have a highly regulated housing market and low values mean that the markets are less regulated.
| Ranking | Jurisdictions | LURE Index | Ranking | Jurisdictions | LURE Index |
| 1 | Roman Forest | 1.02 | 47 | Cleveland | .02 |
| 2 | Sugar Land | .74 | 48 | Shoreacres | .02 |
| 3 | Katy | .67 | 49 | East Bernard | .02 |
| 4 | Fulshear | .63 | 50 | Wharton | .01 |
| 5 | Palacios | .59 | 51 | Huntsville | .01 |
| 6 | Brookside Village | .57 | 52 | Eagle Lake | -.05 |
| 7 | Spring Valley | .54 | 53 | Pasadena | -.06 |
| 8 | Tomball | .54 | 54 | Jersey Village | -.06 |
| 9 | Willis | .50 | 55 | Stafford | -.06 |
| 10 | El Lago | .48 | 56 | Magnolia | -.06 |
| 11 | Seabrook | .48 | 57 | Bunker Hill Village | -.10 |
| 12 | Taylor Lake Village | .44 | 58 | New Waverly | -.11 |
| 13 | Sealy | .41 | 59 | Old River-Winfree | -.11 |
| 14 | Piney Point Village | .40 | 60 | Oak Ridge North | -.14 |
| 15 | Lake Jackson | .38 | 61 | La Porte | -.15 |
| 16 | Orchard | .38 | 62 | Webster | -.15 |
| 17 | El Campo | .38 | 63 | Nassau Bay | -.16 |
| 18 | Shenandoah | .36 | 64 | Dickinson | -.17 |
| 19 | Texas City | .35 | 65 | Clear Lake Shores | -.17 |
| 20 | Iowa Colony | .35 | 66 | Conroe | -.23 |
| 21 | Simonton | .34 | 67 | Brookshire | -.23 |
| 22 | Friendswood | .33 | 68 | Santa Fe | -.24 |
| 23 | Hedwig Village | .31 | 69 | Richmond | -.25 |
| 24 | West University Place | .27 | 70 | Beach City | -.26 |
| 25 | Hillshire | .26 | 71 | West Columbia | -.28 |
| 26 | Missouri City | .26 | 72 | La Marque | -.30 |
| 27 | Dayton | .25 | 73 | Bayou Vista | -.30 |
| 28 | Clute | .23 | 74 | Baytown | -.35 |
| 29 | Sweeny | .23 | 75 | League City | -.37 |
| 30 | Quintana | .20 | 76 | Houston | -.38 |
| 31 | Surfside Beach | .18 | 77 | Angleton | -.39 |
| 32 | Cut and shoot | .17 | 78 | Needville | -.42 |
| 33 | Deer Park | .15 | 79 | Jones Creek | -.45 |
| 34 | Meadows Place | .15 | 80 | Arcola | -.45 |
| 35 | Alvin | .13 | 81 | Southside Place | -.47 |
| 36 | Tiki Island | .13 | 82 | Danbury | -.48 |
| 37 | Manvel | .11 | 83 | Holiday Lakes | -.56 |
| 38 | Freeport | .11 | 84 | Anahuac | -.69 |
| 39 | Pleak | .10 | 85 | Riverside | -.69 |
| 40 | Bay City | .10 | 86 | South Houston | -.70 |
| 41 | Pearland | .09 | 87 | Daisetta | -.73 |
| 42 | Montgomery | .07 | 88 | Pine Island | -.80 |
| 43 | Humble | .07 | 89 | Bonney | -.83 |
| 44 | Mont Belvieu | .07 | 90 | Splendora | -1.01 |
| 45 | Richwood | .07 | 91 | Thompsons | -1.31 |
| 46 | Bellair | .06 | |||
5 Analysis and validation of the LURE index and its sub-indexes
The analysis and validation of the LURE index and its sub-indexes follows a two-sided approach: a) a comparison of the means of the LURE index’s ten sub-indexes across clusters; b) a comparison of the individual variables’ scores (responses); and c) validation by correlating the index with local trait indicators and comparing with an alternative scenario (index). With this strategy it is possible to evaluate in detail the role of each specific variable in the creation of the ten sub-indexes, and the relative importance of the sub-indexes in the definition of the LURE index.
Cluster analysis (CA) is performed before the analysis so that the LURE index could be easily compared with previous studies. Creating clusters makes the interpretation of the results more appropriate for all of the 91 jurisdictions and gives insight into the structure of the dataset. The non-hierarchical method of k-means was selected to create the clusters. Names are assigned to the four obtained clusters based on the degree of regulatory stringency: 1) the most regulated; 2) highly regulated; 3) lightly regulated; and 4) the least regulated.
5.1 Comparing means among clusters
Table 4 summarizes the means of the values of the ten sub-indexes across clusters. It is clear that the differences in the means among clusters are important. This is precisely the purpose of CA: to choose clusters so that the differences between them could be maximized. However, when looking in more detail at the differences between sub-indexes, it can be seen that for every cluster, the differences are not the same across all ten sub-indexes. Based on how the clusters are obtained, the proportion of jurisdictions in each cluster for each sub-index ideally must follow a descending order (the most regulated cluster with the greatest proportion and the least regulated with the least, or lesser, proportion). This is not always the case and for this reason, occasionally the differences in mean values do not follow the same pattern.
| 1 | 2 | 3 | 4 | ||||
| The most | Diffe- | Highly | Diffe- | Lightly | Diffe- | The least | |
| regulated | rence | regulated | rence | regulated | rence | regulated | |
| LGI | .23 | .16 | .07 | .07 | .00 | .86 | -.86 |
| LPAI | .32 | .16 | .16 | .22 | -.06 | 1.06 | -1.12 |
| LAPIR | .35 | .16 | .19 | .30 | -.11 | 1.01 | -1.12 |
| LAHI | .40 | .50 | -.10 | .07 | -.17 | -.13 | -.04 |
| DRI | .63 | .42 | .21 | .73 | -.52 | -.02 | -.50 |
| LSRI | .47 | .41 | .06 | .00 | .06 | 1.63 | -1.57 |
| OSI | .76 | .64 | .12 | .59 | -.47 | .23 | -.70 |
| EI | .21 | -.06 | .27 | .34 | -.07 | 1.11 | -1.18 |
| SRI | .42 | .36 | .06 | .12 | -.06 | .97 | -1.03 |
| LSDPI | .56 | .18 | .38 | .62 | -.24 | 1.61 | -1.85 |
| Median house value | 201,540 | 22,277 | 179,263 | 3,927 | 175,336 | 96,803 | 78,533 |
| Median family income | 92,301 | 13,195 | 79,106 | 3,892 | 75,214 | 24,681 | 50,533 |
| Percentage of families | |||||||
| below poverty line | 7 | -3 | 10 | 0 | 10 | -5 | 15 |
| Percentage White | 64 | 5 | 59 | 0 | 59 | 3 | 56 |
| Percentage Black | 7 | -4 | 11 | 0 | 11 | 0 | 11 |
When comparing clusters 1 and 2, the larger difference can be seen in the OSI sub-index (0.64 standard deviations). It can be noted that the value of the mean of the EI sub-index for cluster 2 is greater than for cluster 1. The reason is that in cluster 1, only 77% of the jurisdictions (17) require the developer to pay an allocable share of the costs of infrastructure improvement, while in cluster 2, 80% (24) of the jurisdictions have this requirement.
The sub-index with the highest difference when comparing clusters 2 and 3 is DRI (0.73 standard deviations). The mean value for the LSRI index is the same in both clusters. The reason for this is that the proportion of jurisdictions with requirements for developers to pay building permit fees and development review fees is the same in both clusters. The greatest difference between the mean values among clusters happens between clusters 3 and 4. The sub-index LSRI has the largest difference, with 1.63 standard deviations. The proportion of jurisdictions in cluster 3 (97 and 63 percent for the two requirements) is more than double those in cluster 4 (45 and 11 percent).
In sub-indexes LHAI and DRI, the mean values for cluster 4 are greater when compared to cluster 3. Although cluster 4 is the least regulated, it does not have a higher proportion of jurisdictions either having multifamily housing built the last two years or requiring developers to include affordable housing. It only has the highest proportion of jurisdictions with manufactured housing built in the last two years, but this is not sufficient to make the mean value for the LHAI sub-index lower than cluster 3. In regards to the DRI sub-index, the mean of cluster 4 is greater than cluster 3 only because the average of the minimum lot size requirement in cluster 4 (natural logarithm of 7.98) is greater than the minimum required in cluster 3 (7.87).
5.2 Individual scores (variables) and the ten sub-indexes
The analysis is performed by comparing responses (scores) to individual variables. Because most of the scores of the indicators are based on a “yes” or “no” response to having a specific regulation, process, or measure, the analysis relied on the proportion of these responses.
- The Local Government Sub-Index (LGI). The LGI sub-index is created based on whether the jurisdictions are either a general law or home rule category of municipality. The variance among the LURE index clusters is similar between clusters 1, 2 and 3. There is no home rule municipality in cluster 4. Due to the important difference between the proportion of jurisdictions being either home rule (39) or general law (52), this variable could still be significant for characterizing the LURE related to housing markets.
- The Local Planning Approval Sub-Index (LPAI). Of the four clusters, number 4 is the
only one having just one jurisdiction with a zoning commission and neighborhood
zoning area. In the other three variables, only two jurisdictions declared having in
place a planning commission, historic commission, and board of adjustment.
Cluster numbers 1, 2 and 3 showed a small difference in the proportion of responses. The variables accounting for these differences are board of adjustments and zoning and planning commissions. In all the clusters, the variable with the highest number of positive responses is having a planning commission. The mean difference is more important between clusters 3 and 4 (1.06 standard deviations).
The high percentage of jurisdictions (at least those in clusters 1, 2 and 3) already having zoning and planning commissions in place could prevent this variable from being a good candidate for future use for measuring variability among communities.
Overall, 78% (71 out of the 91 jurisdictions) ranked by the LURE index answered yes to having a planning commission; 63% to having zoning commissions and a board of adjustments; 36% to having neighborhood zoning areas; and 30% to having a historic commission.
- The Local Planning Approval Requirement Sub-Index (LPAIR). The variable “having
other ordinances governing plats, land development, and subdivisions” has the
highest proportion of jurisdictions answering “yes.” The difference in proportions
among the variables in the same cluster is not remarkable. This small variance
could suggest their removal in future studies for use as indicators capturing variance
among jurisdictions. 87% of jurisdictions (79 out of 91) claimed having “other
ordinances”; 68% have a zoning ordinance; and 66% have a comprehensive plan.
As far as the difference among the clusters’ means for the LURE index, cluster 4 is again the one on the extreme side with a difference of 1.01 standard deviations from cluster 3.
- The Local Affordable Housing Sub-Index (LAHI). The LAHI sub-index is the one of all
ten sub- indexes which has the smallest difference among all clusters (the difference
between the highest and lowest value) with a mean index total value of 0.57
standard deviations (between cluster 1 and 3).
Nonetheless, the variances among variables within the clusters are notable. In cluster 4 (the least regulated), 66.7% of the jurisdictions claimed to have manufactured housing built in the last two years (more than double the value for the other variables and clusters).
Although the variance between clusters is not remarkable, the variables indicate what is happening in the H-GA in terms of affordable housing. From the 91 jurisdictions: 1) 15 (17%) claimed developers are required to include affordable housing; 2) 28 (31%) answered yes to having multifamily housing built the last two years; and 3) 34 (37%) responded yes to having manufactured housing built in the last two years.
- The Density Restriction Sub-Index (DRI). The mean index difference among the clusters
in the DRI sub-index is between clusters 2 and 3 (0.73 standard deviations). The
DRI sub-index is one of the three sub-indexes in which the mean index value for a
cluster does not follow the trend of being lower than the preceding cluster (cluster
4 has a higher value than cluster 3).
The difference between clusters 3 and 4 is due to a higher value for the mean of the natural logarithm of minimum lot size within the city’s ETJ in cluster 4 (7.98) compared to cluster 3 (7.87). The mean values for the other two variables across clusters follow the pattern of descending values (from cluster 1 to 4). This irregularity and the probability of double counting because of the inclusion of highly correlated variables in this sub-index raises questions about the appropriateness of including this variable in the creation of the sub-index.
- The Local Subdivision Requirements Sub-Index (LSRI). LSRI is the sub-index with the
second highest difference between the highest and lowest mean index value (2.04
standard deviations). It is also the only sub-index in which there is no difference
between two clusters and their mean index values (clusters 2 and 3).
The variability between the two variables within the clusters is important, with the lower difference being in cluster 1 (a difference of 13.6 points).
Almost 100 percent of the jurisdictions have the requirement that developers pay building permit fees (84 of 91 jurisdictions). If this continues to be the trend, its inclusion will not signal a difference among jurisdictions.
- The Open Space Sub-Index (OSI). The requirement that developers supply dedicated
space or open space (or pay a fee in lieu of dedication) shows an important variance
among clusters. (The total observed mean index difference between the highest and
lowest value is 1.46 standard deviations). 21 of 22 jurisdictions in cluster 1 have
this type of requirement in place. At the other extreme, just 2 of 9 jurisdictions in
cluster 4 have this requirement.
In general, only 52 of the 91 jurisdictions (57%) have this requirement in place. The low proportion of jurisdictions currently imposing this type of measure makes it feasible to continue to use this indicator for the characterization of the Texas LURE.
- The Exactions Sub-Index (EI). The requirement for the developer to pay an allocable
share of the costs of infrastructure improvement is one of the three sub-indexes in
which the mean index value for a cluster (cluster 2, with a 0.27 value) is higher
when compared to its preceding cluster (cluster 1, with a 0.21 value), making the
mean value difference negative between clusters 1 and 2.
The variance among the clusters for the variables making up the EI sub-index is small among clusters 1, 2 and 3 (0.34 standard deviations). On the other hand, the difference between these three clusters and cluster 4 is high (1.18 standard deviations between clusters 3 and 4).
In general, 61 of 91 jurisdictions (67%) have this type of requirement already in place. The high proportion of jurisdictions in clusters 1, 2 and 3 already having this requirement suggests a trend that could make this variable not a good candidate for characterizing the LURE in the H-GA.
- The Supply Restriction Sub-Index (SRI). Because of the difference in the diversity of
variables included in the SRI sub-index, this is probably the sub-index with the
most discrepancies in the variables within the clusters and among the clusters.
In cluster 4 the sub-index does not record any measure for four of the five variables (the other variable has just one jurisdiction). Having a measure which requires adequate service levels for residential development or service capacity as a condition of approval of residential development is the variable with the most jurisdictions in the analysis (56 of 91). On the other hand, the variable having the least jurisdictions is a measure which re-designates or rezones residential land to agriculture or open space (13 of 91). The variance and the small number of jurisdictions recorded as implementing these measures make these variables good candidates for continued inclusion in the LURE index.
- The Local Standard Development Perception Sub-Index (LSDPI). The LSDPI sub-index is the one with the highest mean difference index value among clusters (2.41 standard deviations). In addition, this sub-index is also the one having the highest difference between two clusters in their mean index values (clusters 3 and 4 have a 1.61 standard deviation difference).
5.3 Validation of the LURE index
Table 4 shows the mean values of local traits such as median housing values, median family income, percentage of families below poverty line, and percentage of White and Black population. Cluster 1, the most regulated, is where the most valuable houses are located. The median house value ($201,540) in this cluster is almost three times the value of cluster 4 ($78,533), the least regulated. Regarding income, the difference between cluster 1 and the other three clusters is also noticeable. Median family income is almost double in cluster 1 ($92,301) when compared to cluster 4 ($50,533). Poverty is another trait in which the differences are remarkable. The most regulated cluster has the smallest percentage of families below poverty line (7%). It is half the proportion compared to the least regulated cluster (15%) and 3 percentage points below the highly and lightly regulated clusters.
In terms of distribution of races, there is a pattern, although small, in which cluster 1 has a higher percentage of White population when compared to the other clusters. Cluster 4 has a higher percentage of Black population when compared to cluster 1.
Table 5 shows the correlation values between the LURE index and the local traits. Although the coefficients are low, the statistical correlation shows that four out of the five variables have a significant relationship with the regulatory stringency of the jurisdictions characterized by the LURE index. The proportion of Black population, families below poverty level, and median family income have a statistically significant relation with the LURE index at the 0.05 level. The median house value relation is significant at the 0.10 level. Proportion of White population does not show a significant relation.
These results allow agreement with the findings of other authors that the null hypothesis of a lack of relation between the LURE index and these four local indicators can be rejected. These correlation results validate the appropriateness of indexes as measures in characterizing LUREs for housing markets (Baldassare, Protash 1982, Bates, Santerre 1994, Burnell, Burnell 1989, Donovan, Neiman 1992, Gyourko et al. 2008).
| Indicators (all 2010) | Pearson Correlation (Sig. 2-tailed)
| ||
| Percentage Black | -.155* | (.143) | |
| Percentage of families below poverty line | -.224* | (.032) | |
| Percentage White | .112 | (.289) | |
| Median family income | .260* | (.013) | |
| Median house value | .170+ | (.106) | |
The second validation step taken for this analysis was to contrast the rankings of the cities based on the LURE index against another index alternative or scenario, in this case, an equal weighting assumption. Equal weighting is the second most used assumption in the creation of indexes of regulatory stringency. It is important to clarify that the creation of an index involves multiple assumptions during the process of creating it; therefore, an index reflects those assumptions and does not necessarily always capture the real phenomena measured.
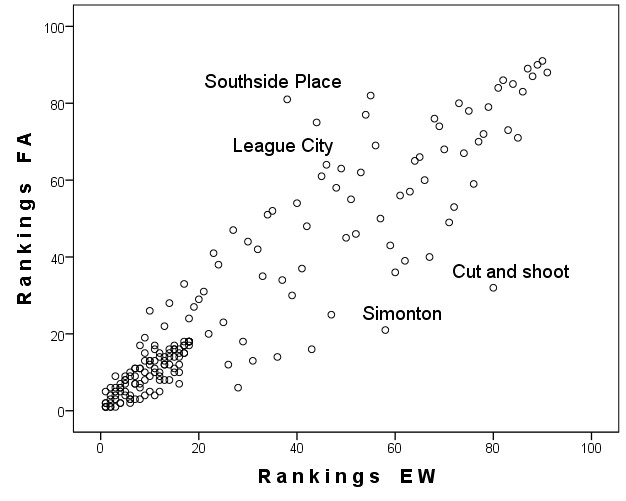
The correlation between the LURE index and the equal weighting alternative is statistically significant (Spearman correlation = 0.922). Scatterplot in Figure 2 shows how fluctuations are more present in the middle half of the ranked jurisdictions. The most (upper quartile) and least regulated (bottom quartile) jurisdictions for both indexes are the most robust to change in the weighting assumptions. When looking at the differences (number of shifts in ranking from one index to the other for any particular jurisdiction), 56 out of the 91 jurisdictions (62%) have 10 or less shifts on their rankings. 20 jurisdictions (22%) have a shift between 11 and 20. 11 jurisdictions (12%) have a shift of between 20 and 30. Only 4 (4%) have a change of between 30 and 50 places. If 62% of the jurisdiction changing less than 10 places between the two weighting methods is acceptable, this means that either EW or FA weightings assumptions yield similar ranking results for the creation of the indexes to characterize land use regulatory environments for housing markets.
Like other indexes’ results, not all cities were affected in the same way in their rakings under the two alternatives. Figure 2 allows us to see which jurisdictions are the most impacted by these two weighting methods. The cities of Cut and Shoot, Southside Place, Simonton, and League City, which have a difference between the two rankings of more than 30 places, are the four jurisdictions with the most extreme variation. On the opposite side, two jurisdictions (Spring Valley and Jones Creek) got the same ranking in both indexes.
6 Conclusions
The LURE index has been created with the objective of validating the use of an index as an appropriate composite measure to characterize the stringency of land use regulatory environments for housing markets in metropolitan areas.
Factor analysis proved that the LURE index is a measure capable of capturing the latent factors linking housing markets and land use regulations. At least four to five dimensions (from the ten established in the theoretical framework) are detected by the statistical procedure as capturing more than 65% of the total variance in the sample of the LURE index data. The correlation between the index and the specific local traits showed statistical significance at the 0.10 and 0.05 significant levels. These results validate similar correlations found in the literature.
The decomposition analysis, performed to ascertain the role of each variable, confirmed the multi- dimensional nature of land use regulations for housing markets. The analysis of the LURE index results shows that highly regulated jurisdictions tend to be so almost across the board (in every sub-index value). In general, highly regulated jurisdictions are richer and have much higher housing values than the lightly and least regulated. Median family income in highly regulated jurisdictions is higher, by more than $40,000, compared to the least regulated. Median house value in highly regulated jurisdictions is almost three times the value compared to the least regulated. Highly regulated jurisdictions have a greater fraction of White households, but the difference is modest in contrast to the least regulated jurisdictions.
The statistical correlation between the LURE index and an equal weighting alternative validates the robustness to change in the weighting assumption of the index. Further research could involve the use of more scenarios, taking into account other procedures not used in this study (e.g. non-compensatory aggregation, excluding other variables).
In summary, the results of the creation and assessment of the LURE index verify that an index of these characteristics is a valid and reliable measure to characterize the multi-dimensional nature of LUREs for housing markets.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
References
AIP – American Institute of Planners (1976) Survey of state land use planning activity. Report to the US Department of Housing and Urban Development. American Institute of Planners, Washington, DC
Baldassare M, Protash W (1982) Growth controls, population growth, and community satisfaction. American Sociological Review 47[3]: 339–346. CrossRef.
Bandura R (2008) A survey of composite indices measuring country performance: 2008 update. A undp/ods working paper, united nations development programme, office of development studies, http://old.usc.ac.ir/IPPWebV1C035/TemplateFileFolder/10-8-2013/OriginalFolder/0a6e29c4-1fa6-4496-a362-000f0851d4fc_indices_2008_bandura.pdf
Bates LJ, Santerre RE (1994) The determinants of restrictive residential zoning: some empirical findings. Journal of Regional Science 34[2]: 253–263. CrossRef.
Black JT, Hoben J (1985) Land price inflation. Urban Geography 6[1]: 27–49
Burnell BS, Burnell JD (1989) Community interaction and suburban zoning policies. Urban Affairs Quarterly 24[3]: 470–482. CrossRef.
Cutsinger J, Galster G, Wolman H, Hanson R, Towns D (2005) Verifying the multi-dimensional nature of metropolitan land use: Advancing the understanding and measurement of sprawl. Journal of Urban Affairs 27[3]: 235–259. CrossRef.
Dain A (2006) Reference guide to residential land-use regulation in eastern massachusetts: A study of 187 communities. Rappaport Institute for Greater Boston, Harvard University, Pioneer Institute for Public Policy Research, Cambridge/Boston, MA
Donovan T, Neiman M (1992) Community social status, suburban growth, and local government restrictions on residential development. Urban Affairs Quarterly 28[2]: 323–336. CrossRef.
Estevez Jimenez L (2012) Government regulations and housing markets: An index to characterize local land use regulatory environments for residential markets in the Houston – Galveston area. Doctoral dissertation, Texas A&M University
Freudenberg M (2003) Composite indicators of country performance: A critical assessment. OECD science, technology and industry working papers, no. 2003/16, OECD Publishing, Paris. CrossRef.
Glaeser EL, Ward BA (2009) The causes and consequences of land use regulation: Evidence from greater boston. Journal of Urban Economics 65[3]: 265–278. CrossRef.
Glickfeld M, Levine N (1992) Regional growth and local reaction: The enactment and effects of local growth control and management measures in California. Lincoln Institute of Land Policy, Cambridge, MA
Green RK (2009) Commentary. In: Glaeser EL, Quigley JM (eds), Housing Markets and the Economy: Risk, Regulation, and Policy. Lincoln Institute of Land Policy, Cambridge, MA. CrossRef.
Gyourko J, Saiz A, Summers A (2008) A new measure of the local regulatory environment for housing markets: The wharton residential land use regulatory index. Urban Studies 45[3]: 693–729. CrossRef.
HUD – US Department of Housing and Urban Development (1991) Report to congress on rent control. Office of Policy Development and Research: US Department of Housing and Urban Development. Washington, DC
Ihlanfeldt KR (2007) The effect of land use regulation on housing and land prices. Journal of Urban Economics 61[3]: 420–435. CrossRef.
Knaap G (1998) The determinants of residential property values: Implications for metropolitan planning. Journal of Planning Literature 12[3]: 267–282. CrossRef.
Lewis P, Neiman M (2000) Residential development and growth control policies: Survey results from cities in three California regions. Occasional paper, Public Policy Institute of California, San Francisco
Linneman P, Summers A, Brooks N, Buist H (1990) The state of local growth management. Working paper no. 81, Wharton Real Estate Center, The Wharton School, University of Pennsylvania
Malpezzi S (1996) Housing prices, externalities, and regulation in u.s. metropolitan areas. Journal of Housing Research 7[2]: 209–241
Malpezzi S (2009) Commentary. In: Glaeser EL, Quigley JM (eds), Housing Markets and the Economy: Risk, Regulation, and Policy. Lincoln Institute of Land Policy, Cambridge, MA
Nardo MTS, Saltelli A, Andropoulos C, Buescher R, Karageorgos G, Latvala A, Noel F (2004) The e-business readiness composite indicator for 2003: A pilot study. European Commission, DG Joint Research Centre, EUR 21294 EN, http://publications.jrc.ec.europa.eu/repository/bitstream/JRC28490/EUR 21294 EN.pdf
NMHC – National Multi Housing Council (1982) Rent control activities through may 31, 1982. National Multi Housing Council, Washington, DC
Nunnally JC (1978) Psychometric theory (2nd ed.). McGraw-Hill, New York
Nunnally JC, Bernstein IH (1994) Psychometric theory (3rd ed.). McGraw-Hill, New York
Pendall R, Puentes R, Martin J (2006) From traditional to reformed: A review of the land use regulations in the nation’s 50 largest metropolitan areas. Metropolitan Policy Program, The Brookings Institution, https://www.brookings.edu/wp-content/uploads/2016/06/20060802_Pendall.pdf
Quigley JM, Raphael S (2005) Regulation and the high cost of housing in California. American Economic Review 95[2]: 323–328. CrossRef.
Quigley JM, Rosenthal LA (2005) The effects of land-use regulation on the price of housing: What do we know? What can we learn? Cityscape 8[1]: 69–137
Segal D, Srinivasan P (1985) The impact of suburban growth restrictions on U.S. housing price inflation, 1975-78. Urban Geography 6[1]: 14–26. CrossRef.
Somerville CT (1999) The industrial organization of housing supply: Market activity, land supply and the size of homebuilder firms. Real Estate Economics 27[4]: 669–694. CrossRef.
 © 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)
© 2018 by the authors. Licensee: REGION - The Journal of ERSA, European
Regional Science Association, Louvain-la-Neuve, Belgium. This article is distributed under the terms and conditions of the Creative
Commons Attribution, Non-Commercial (CC BY NC) license (http://creativecommons.org/licenses/by-nc/4.0/)